【论文阅读20】-CNN-Attention-BiGRU-滑坡预测
这篇论文主要探讨了基于深度学习的滑坡位移预测模型,结合了MT-InSAR(多时相合成孔径雷达干涉测量)观测数据,提出了一种具有可解释性的滑坡位移预测方法。
[1] Zhou C, Ye M, Xia Z, et al. An interpretable attention-based deep learning method for landslide prediction based on multi-temporal InSAR time series: a case study of xinpu landslide in the TGRA[J]. Remote Sensing of Environment, 2025, 318: 114580.
期刊
Remote Sensing of Environment
作者:
Chao Zhoua,b,Mingyuan Yea,Zhuge Xiac,b,*,Wandi Wangb,Chunbo Luod,Jan-Peter Mullere
第一作者
Chao Zhou(R)
作者单位:
a 中国地质大学(武汉),地理与信息工程学院,武汉 430078,中国
b 德国地学研究中心(GFZ),遥感与地理信息科学部,特雷格拉芬贝格,波茨坦 14473,德国
c 河海大学,地球科学与工程学院,南京 211100,中国
d 英国埃克塞特大学,计算机科学系,埃克塞特 EX4 4QF,英国
e 英国伦敦大学学院(UCL),马拉德空间科学实验室,空间与气候物理系,霍尔姆伯里圣玛丽,萨里 RH5 6NT,英国
-
问题背景与目标:滑坡作为一种常见的地质灾害,其位移预测对于灾害预警和防治至关重要。传统的滑坡位移预测方法存在一定的局限性,特别是在处理复杂的非线性和非平稳数据时。本文旨在通过深度学习方法提高滑坡位移预测的准确性,并增强模型的可解释性。
-
模型方法:
- 论文提出了一种耦合的CNN-Attention-BiGRU模型。CNN(卷积神经网络)用于从多维度数据中提取特征,Attention机制则增强了时间特征的提取能力,BiGRU(双向门控循环单元)则利用历史信息来提高滑坡位移预测的准确性。
- CNN-Attention机制帮助模型更好地关注重要的时序特征,增强了对关键触发因素的响应能力。
- VMD(变分模态分解)被用于时序分解,帮助有效分离趋势项和季节性成分,进而提高预测精度。
-
实验与结果:
- 通过在新浦滑坡区域进行实验,论文展示了该模型在不同监测点上的预测效果,并与传统的CNN-BiGRU、BiGRU和BiLSTM等模型进行了比较。
- 结果表明,所提模型在滑坡位移预测方面表现优异,尤其在大幅度位移变化的时期,预测精度显著提高。
-
可解释性分析:
- 通过CNN-Attention模型,论文揭示了降水量和RWL(水位变化)等因素在不同时间段对滑坡变形的影响,特别是在滑坡快速运动的时期。注意力机制帮助模型关注历史触发因素对当前位移的影响,从而提高了模型的可解释性。
- 论文还通过热图展示了不同时间戳的特征权重,分析了这些因素在预测中的相对重要性。
-
结论:
- 本文提出的CNN-Attention-BiGRU模型能够有效提高滑坡位移的预测精度,同时通过可解释性分析,增强了模型的透明度,能够揭示滑坡变形与环境因素(如降水量和水位变化)之间的动态关系。
- 该方法在多学科灾害风险减缓中具有广泛的应用潜力,尤其适用于地质灾害预测和预警系统。
总的来说,本文的贡献在于结合深度学习和MT-InSAR数据,提出了一种高效且可解释的滑坡位移预测模型,为地质灾害的早期预警和风险评估提供了新的思路和方法。
【论文阅读20】-CNN-Attention-BiGRU-滑坡预测
- **摘要**
- **1. 引言**
- **2. 研究区**
- **3. 方法**
- **3.1 InSAR 数据处理**
- **3.2 位移时间序列分解**
- **3.3 基于注意力机制的深度学习建模**
- **3.3.1 趋势项预测**
- **3.3.2 季节项预测**
- **3.4 精度评价与对比**
- 4. 结果分析
- 4.1 MT-InSAR 形变与环境配置
- 4.1.1 边坡不稳定性与诱发因素
- 4.1.2 多个水文年的形变对比
- 4.1.3 单一水文年(2017 年)内的统计比较
- 4.1.4 滑坡运动验证与分类
- **4.2 滑坡变形预测**
- **4.2.1 位移时间序列的分解**
- 4.2.2 趋势与季节性分量预测
- 4.2.3 滑坡位移时间序列的组成
- 4.2.4 我们方法的鲁棒性评估
- 5. 讨论
- 5.1 地质特性与触发因素
- 5.2 基于机器学习的变形预测
- 5.3 CNN-Attention模型特征权重的特点
- 6. 结论
全文翻译
摘要
滑坡变形的预测对于预警系统至关重要。传统的岩土原位监测由于高成本和在大范围区域内的空间限制,其应用受到了制约。近年来,结合遥感数据的深度学习方法在滑坡预测研究中日益普遍,但这类方法往往存在“黑箱”问题。
为解决这一问题,本文提出了一种结合注意力机制和多时相干涉合成孔径雷达(MT-InSAR)技术的可解释深度学习滑坡位移预测框架。首先,利用Copernicus Sentinel-1 SAR影像,通过MT-InSAR提取滑坡的位移时间序列。随后,采用变分模态分解(VMD) 将非线性位移时间序列分解为趋势项、季节项和噪声项。针对趋势项和季节项,分别使用自回归积分滑动平均模型(ARIMA) 与双向门控循环单元(BiGRU) 进行预测;预测输入则通过分析滑坡影响因子确定。
本研究以中国三峡库区的新铺滑坡为例,验证并评估所提出方法的有效性,并与现有模型进行了对比。结果表明,CNN-Attention-BiGRU算法能够有效捕捉滑坡变形与其诱因之间的非线性关系,其预测精度优于传统深度学习模型(如BiLSTM、BiGRU和CNN-BiGRU),均方根误差(RMSE)提升21%—55%,平均绝对误差(MAE)提升23%—56%。
通过引入注意力机制的深度学习方法,本文在建模中考虑了滑坡变形的内在机制,并发现关键预测因子的相对重要性在每年4月至8月最为显著,从而实现了对大型库区滑坡动力学的更高效、更精准预测。
文章信息
编辑:Jing M. Chen
关键词:卫星遥感、滑坡位移预测、注意力机制、CNN-Attention-BiGRU、可解释深度学习
1. 引言
引出话题
滑坡是全球最严重的地质灾害之一,其发生范围广、频率高、破坏性强(Lacroix 等,2020;Highland 和 Bobrowsky,2008)。由于地质条件复杂,滑坡多发于山地和丘陵地区,且常与强烈的构造活动相关,对生命财产构成严重威胁。滑坡位移的监测尤为关键,因为它能直接反映出周期性变化及整体变形趋势,是滑坡预警与风险防控的主要依据(Zhou 等,2022b)。准确预测滑坡位移,有助于提前采取防范措施,有效减轻次生灾害,显著降低人员伤亡和经济损失。
InSAR优势
传统的地面位移监测方法,如水准测量或全球导航卫星系统(GNSS)技术,因其数据点数量有限,只能反映滑坡状态和运动趋势。此外,GNSS 监测设备的高人工成本也限制了其在大范围、多个滑坡体监测中的应用。干涉合成孔径雷达(InSAR)技术的出现,为滑坡监测带来了新的机遇。InSAR 具备全天候、全天时、高精度遥感监测地表微小变形的能力(Zhou 等,2024),可实现大范围、系统性的监测,突破了传统手段的局限性,大大提升了滑坡运动预测的能力(Xia 等,2023;Bayer 等,2017;Bozzano 等,2011)。
研究现状
过去的研究多致力于构建不同的统计或物理模型来预测滑坡运动时间序列(Carlà 等,2017)。随着人工智能技术的发展,机器学习与深度学习方法在处理多变量数据与挖掘隐藏数据关系方面展现出巨大潜力,为提升滑坡位移时间序列预测的精度提供了良好基础。例如,Carlà 等(2017)使用短期与长期移动平均及指数平滑函数对滑坡失稳进行预测;Zhou 等(2018)将核极限学习机(KELM)应用于趋势项与季节项的预测,有效提升了树坪滑坡的动力学模拟能力。
挑战
然而,预测基于 InSAR 的滑坡时间序列时,位移变化往往受多种因素共同影响,这使得在不丢失信息的前提下管理复杂多变量之间的关系成为一大挑战(Ma 和 Mei,2024)。因此,越来越多的研究开始将环境诱发因素与运动学特征结合,以提高预测能力(Zhang 等,2024)。Shihabudheen 和 Peethambaran(2017)构建了融合经验分解、降雨和库水位影响的极限学习自适应神经模糊推理模型,用于预测三峡库区白家堡滑坡的位移变化。Han 等(2021)则通过引入滑坡致因因子,提出了基于支持向量机(SVM)的混合机器学习预测模型,用于应对滑坡位移的快速变化。
引出CNN和GRU,以及存在问题
尽管卷积神经网络(CNN)在提取多变量关系方面表现优异,但往往难以捕捉时间依赖性,导致特征损失(Gasparin 等,2022)。为解决此问题,Zhang 等(2022)采用门控循环单元(GRU)模型对九仙坪滑坡的位移进行预测,成功捕捉了周期变化与变形模式,同时使用自适应动量估计(Adam)优化器缓解了噪声和梯度稀疏问题。尽管深度学习方法能处理复杂的多变量问题,但由于其内部处理机制难以解释,常被视为“黑箱”,这也成为其在实际应用中难以普及的原因之一(Von Eschenbach,2021)。
引出Attention
针对上述问题,可引入注意力机制,为不同特征分配不同权重,从而强化时间序列特征提取并提升模型的可解释性。在地球科学的应用中,注意力机制被广泛用于提升 CNN、循环神经网络(RNN)及其与长短期记忆网络(LSTM)结合方法的可解释性。例如,Zhang 等(2021b)和 Li 等(2021)分别使用 GRU 和地理加权 LSTM 模型,成功捕捉了影响地表沉降和边坡失稳的关键时空动态,这些动态来自于 InSAR 监测数据。CNN 模型也展现出良好潜力,例如 Ma 等(2020)利用深度卷积神经网络准确预测 InSAR 时间序列变形,Rouet-Leduc 等(2021)使用卷积自编码器检测毫米级地表形变。Lattari 等(2022)提出结合 RNN 和 LSTM 的方法,用于 InSAR 时间序列的变点检测,在模拟与真实数据中均验证了其在地震断层、地面沉降和滑坡监测中的有效性。近期,Zhou 等(2024)将 GRU 与多时相 InSAR(MT-InSAR)数据结合,实现了更高精度的大范围滑坡预测。
算法存在问题
但 GRU 在处理长序列时可能表现不佳,而 LSTM 的计算复杂度高、难以解释决策过程,且对训练数据量有较高需求。因此,迫切需要具备可解释性的深度学习方法来预测库区滑坡运动。
本文方法
本研究提出了一种基于注意力机制的深度学习方法用于预测滑坡变形。我们的目标是构建一个能够提升预测精度与可解释性的滑坡运动学预测模型。引入通道注意力机制,用于增强滑坡运动学时间序列特征的提取能力;采用能捕捉长序列依赖关系的双向门控循环单元(BiGRU)模型,便于全面分析历史信息。
最终我们提出了基于 MT-InSAR 时间序列的 CNN-Attention-BiGRU 滑坡预测方法。以受到降雨和库水位波动影响显著的三峡库区新铺滑坡为研究对象,本研究构建的预测框架有效融合了 InSAR 监测、深度学习、聚类分析与预测建模技术,提升了滑坡综合分析与预测能力。实验证明,所提出的算法能精准捕捉诱因与滑坡运动之间复杂的非线性关系,其预测精度(以 RMSE 和 MAE 衡量)显著优于传统模型,如 BiLSTM、BiGRU 和 CNN-BiGRU。
此外,该方法还能深入揭示影响滑坡动力学的环境触发机制与演变过程。我们相信,该方法对于滑坡灾害风险降低具有重要价值,尤其适用于库区滑坡,并在遥感领域具有广阔的应用前景。
2. 研究区
新铺滑坡位于三峡库区(TGRA)奉节县新铺村,地处长江南岸,如图1所示。该滑坡距离三峡大坝约158公里,是一处典型的水库浸没型滑坡(Ye 等,2024)。滑坡整体上部狭窄、下部宽阔,呈现出光滑层中夹有微切层的结构,从平面上看如同扇形展开。其前缘高程为81–85米,而后缘最高点海拔约为810米,前缘最低点为三峡库区枯水期的水位,两者间的相对高差超过630米。前缘主要由松散土体构成,长期受到长江水体冲刷,在重力作用下发生了多次滑动事件,形成了多级台阶状地貌。

新铺滑坡体内分布有大量居民住宅,这些建筑已出现墙体开裂、地面沉降、倒塌、滑移和沟道变形等明显灾害迹象(Zheng 等,2023)。滑坡区域地貌以中低山沟谷为主,主要由构造侵蚀和剥蚀作用塑造。地势整体自南向北下降,从长江岸线逐步下切。区域内山脊多呈东北至东方向展布,长江在枯水期的河面宽度约为1.5公里。该段河谷呈现出明显的不对称性:北岸为逆坡,坡度较陡,约为30–50°,沟壑发育;而南岸为顺坡,整体坡度为15–20°。滑坡体堆积形成阶梯状斜坡面,沟壑深度为10–20米,坡度与斜坡面基本一致。
3. 方法
图2展示了所提出的滑坡位移时间序列预测方法的流程图。该方法基于注意力机制的深度学习方法,采用四个步骤构建滑坡位移预测流程:
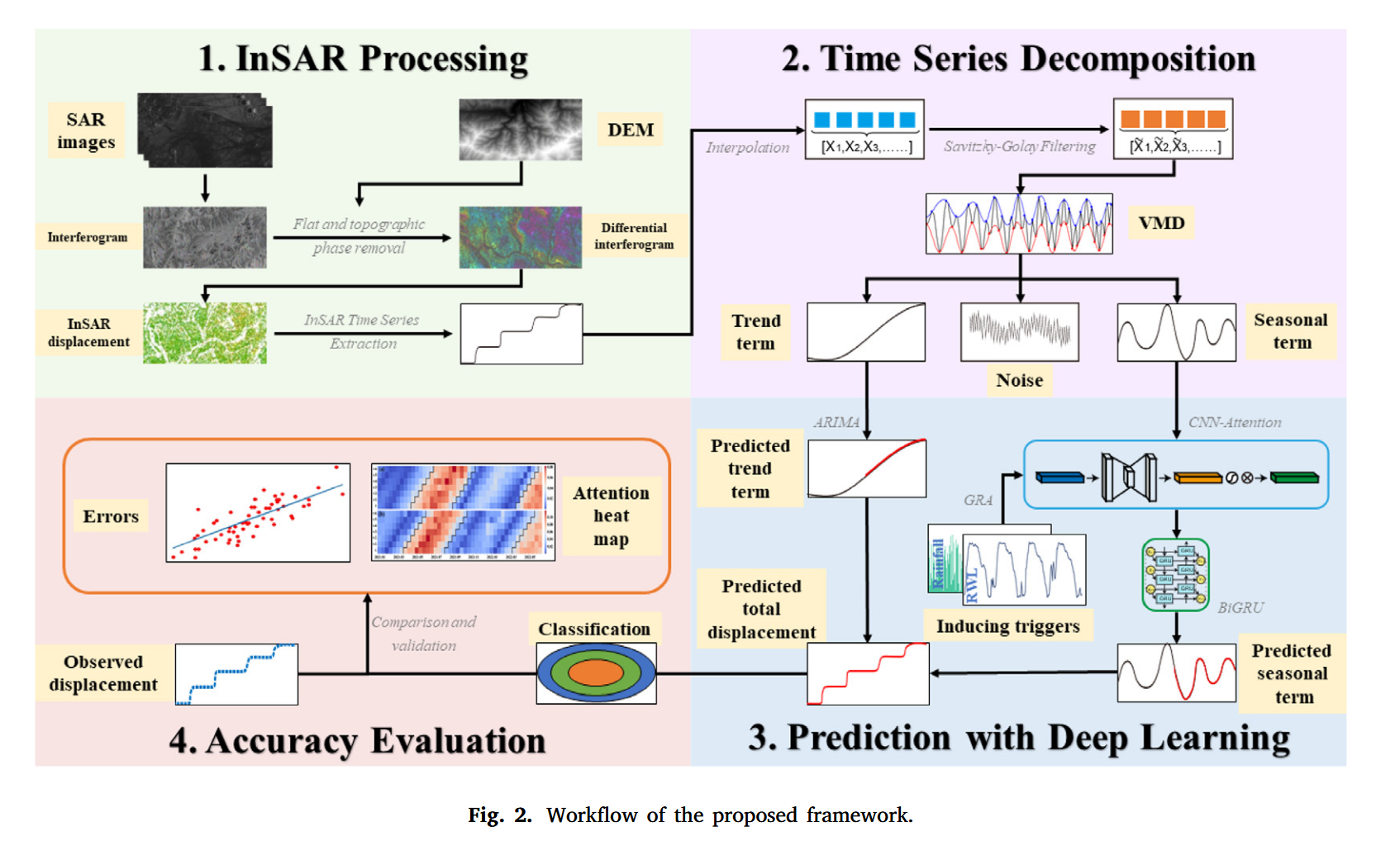
(i)MT-InSAR 数据处理:
首先,针对新铺滑坡,收集了2016年3月至2022年6月期间的 Sentinel-1 雷达影像数据,进行 MT-InSAR 处理。图像配准和地形相位去除使用的是分辨率为30米(即一弧秒)的 Copernicus DEM(Bielski 等,2024)。
(ii)时间序列滤波与分解:
然后对 InSAR 获取的滑坡位移时间序列进行插值和平滑处理,以提取其瞬时变化特征与长期运动趋势。经过滤波后的时间序列进一步被分解为趋势项与季节项。
(iii)趋势与季节项预测建模:
趋势项采用自回归滑动平均整合模型(ARIMA)进行预测,而季节项则先与诱发因子序列进行相关性分析,然后使用 CNN-Attention-BiGRU 模型进行预测。为了构建 CNN-Attention-BiGRU 模型,我们收集了三峡库区每日库水位(RWL)数据,以及来自新铺雨量站的降雨数据。诱发因子被划分为五个序列:12天、24天和36天的累积降雨量;12天的平均库水位;以及12天平均库水位的变化量。最终,通过将趋势项与季节项的预测结果进行叠加重构,得出新铺滑坡的位移预测值。
(iv)注意力机制解释分析与模型评估:
最后,我们对 CNN-Attention-BiGRU 模型中获得的注意力权重层进行分析,从而提升模型的可解释性与透明度。整个方法流程建立了一种可解释的滑坡位移预测模型。
此外,为了验证所提模型的预测准确性,我们采用了均方根误差(RMSE)、平均绝对误差(MAE)以及决定系数(R²)作为评价指标。为进一步评估模型性能,我们还与其他三种模型进行了对比分析,包括 BiGRU、BiLSTM 和 CNN-BiGRU 模型。
3.1 InSAR 数据处理
在多时序干涉合成孔径雷达(MT-InSAR)处理过程中,本研究共使用了168景 C波段 Sentinel-1 卫星图像,这些图像均为干涉宽幅(IW)模式,覆盖时间为2016年3月至2022年6月。Sentinel-1 IW 模式图像的空间分辨率约为方位向 2.3 2.3 2.3 米、距离向 14.0 14.0 14.0 米。需要注意的是,针对本研究滑坡区域,仅获取到了升轨影像,因此对沿西北—东南方向的地面变形不敏感。
传统 InSAR 技术存在两个主要局限性:首先,它受到去相关效应(decorrelation effects)的影响。InSAR 干涉图像是两个配准后的复数 SAR 图像(包含强度和相位信息)的互相关结果,其在雷达波长尺度上反映了后向散射特征的变化。当 InSAR 相干性下降时,数据质量会受到影响(Jacob 等,2020)。其次,变形监测结果容易受到多种误差源影响,例如用于地形相位去除的数字高程模型(DEM)精度不足、大气延迟、轨道误差、相位解缠错误以及其他噪声来源(Xia 等,2023;Barra 等,2017)。当地表变形幅度较小时,这些噪声甚至可能完全掩盖有效信号,导致监测变得异常困难。
MT-InSAR 技术通过引入足量覆盖同一研究区域的图像序列,有效克服了传统 InSAR 的上述限制,从而去除了与变形无关的相位信息。相关处理流程可参考 Fattahi 等(2016)所提出的方法。MT-InSAR 可降低相干性丢失的影响和噪声相位成分的干扰,即使在植被覆盖或半植被环境下,也可实现较高的监测精度。
本研究主要采用了小基线集(Small Baseline Subsets,SBAS)方法,并利用分布式散射体(Distributed Scatterers, DS)建立了小空间及时间基线网络,以减少时间去相关(Anderssohn 等,2009)。DS 被定义为与其邻域像素具有相似统计特性的像素点。SBAS 处理基于 STAMPS/MT-InSAR 软件实现(Hooper,2008;Hooper 等,2004),用于获取新铺滑坡的位移时间序列。
3.2 位移时间序列分解
为了更好地预测滑坡运动特征,我们将时间序列分解为趋势项与季节项,从而更准确地表征其长期变化与短期扰动。在对 InSAR 获取的滑坡位移时间序列进行分解前,必须进行预处理以实现时间轴的均匀化,因为 SAR 图像获取存在间隔不均问题,而深度学习模型需要时间上规则分布的数据输入。
具体地,我们将覆盖168天的位移序列进行插值处理,形成191个时间节点,等效于 Sentinel-1 的12天重访周期。当某时刻缺失 SAR 数据时,采用线性插值方法基于前后时刻的数据进行估算,参考 Tomás 等(2016)的方法。
滑坡的累计位移序列可表示为:
C ( t ) = T ( t ) + P ( t ) (1) C(t) = T(t) + P(t) \tag{1} C(t)=T(t)+P(t)(1)
其中, C ( t ) C(t) C(t) 为累计位移, T ( t ) T(t) T(t) 为趋势项,主要受滑坡自身的地质结构影响, P ( t ) P(t) P(t) 为季节项,主要受周期性环境诱发因子(如降雨、水位)影响。
插值完成后,应用 Savitzky-Golay 滤波器对时间序列进行平滑处理,以剔除异常值。该滤波器能够提升信号平滑度,降低噪声干扰(Schafer,2011)。其滤波效果受窗口宽度选择的影响,可适用于多种场景。
之后,我们采用 变分模态分解(Variational Mode Decomposition, VMD) 方法对位移时间序列中的趋势与季节性成分进行分解。VMD 模型的数学表达如下:
min { u k } , { ω k } { ∑ k ∥ ∂ t [ ( δ ( t ) + j π t ) ⋅ u k ( t ) ] e − j ω k t ∥ 2 2 } (2) \min_{\{ u_k \}, \{ \omega_k \}} \left\{ \sum_k \left\| \partial_t \left[ \left( \delta(t) + j \frac{\pi}{t} \right) \cdot u_k(t) \right] e^{-j \omega_k t} \right\|_2^2 \right\} \tag{2} {uk},{ωk}min{k∑ ∂t[(δ(t)+jtπ)⋅uk(t)]e−jωkt 22}(2)
u k ( t ) = A k ( t ) cos ( ϕ k ( t ) ) (3) u_k(t) = A_k(t) \cos(\phi_k(t)) \tag{3} uk(t)=Ak(t)cos(ϕk(t))(3)
s.t. ∑ k u k = f (4) \text{s.t.} \quad \sum_k u_k = f \tag{4} s.t.k∑uk=f(4)
其中, u k ( t ) u_k(t) uk(t) 表示在时间 t t t 的模态函数集合, ω k ( t ) \omega_k(t) ωk(t) 为每个模态函数的中心频率, k k k 为模态分解的总个数, δ ( t ) \delta(t) δ(t) 描述各子模态函数的中心频率。
VMD 是一种能够通过多分辨率分解非线性信号的方法(Humphrey 等,1996),可同时处理非递归和递归信号,实现变分模态信号的频带分离。VMD 分解后可获得多个具有不同频率特性的内禀模态函数(IMFs),通过重构可分别得到趋势项、季节项以及残差项。
残差部分主要受人为活动及其他随机噪声影响。根据实地调查与对新铺滑坡的综合分析,本研究不对该部分进行进一步建模分析。
3.3 基于注意力机制的深度学习建模
3.3.1 趋势项预测
在本研究中,滑坡位移时间序列的趋势项与季节项分别采用 ARIMA 模型与 CNN 模型进行建模与预测。
首先,趋势项采用 自回归积分滑动平均模型(ARIMA) 进行建模。ARIMA 模型基于时间序列的历史数据,通过自相关分析与差分处理构造时间序列片段,进而预测未来位移值。ARIMA 模型由三部分组成:自回归(AR)、差分整合(I)和移动平均(MA)。
- 自回归部分考虑前期观测值对当前值的影响;
- 差分部分通过一阶或二阶差分等方式消除非平稳性;
- 移动平均部分则考虑前期预测误差对当前值的影响(Peng 等,2024)。
ARIMA 模型的数学表达如下(Contreras 等,2003):
{ AR: Y t = c + ϕ 1 Y t − 1 + ϕ 2 Y t − 2 + ⋯ + ϕ p Y t − p + ε t MA: Y t = μ + ε t + θ 1 ε t − 1 + θ 2 ε t − 2 + ⋯ + θ q ε t − q (5) \begin{cases} \text{AR:} \quad Y_t = c + \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \cdots + \phi_p Y_{t-p} + \varepsilon_t \\ \text{MA:} \quad Y_t = \mu + \varepsilon_t + \theta_1 \varepsilon_{t-1} + \theta_2 \varepsilon_{t-2} + \cdots + \theta_q \varepsilon_{t-q} \end{cases} \tag{5} {AR:Yt=c+ϕ1Yt−1+ϕ2Yt−2+⋯+ϕpYt−p+εtMA:Yt=μ+εt+θ1εt−1+θ2εt−2+⋯+θqεt−q(5)
其中:
- Y t Y_t Yt 为时间序列值;
- c c c 是常数项;
- ϕ 1 , ϕ 2 , … , ϕ p \phi_1, \phi_2, \ldots, \phi_p ϕ1,ϕ2,…,ϕp 是 AR 部分的参数,描述当前值与过去 p p p 个值之间的关系;
- θ 1 , θ 2 , … , θ q \theta_1, \theta_2, \ldots, \theta_q θ1,θ2,…,θq 是 MA 部分的参数,描述当前值与过去 q q q 个误差之间的关系;
- ε t \varepsilon_t εt 为时间点 t t t 的误差项。
3.3.2 季节项预测
图 3a 展示了本研究中所采用的 CNN-Attention-BiGRU 模型的流程图。在该模型中,输入数据为五种诱发因子的季节项时间序列,首先通过 一维卷积 的 CNN 层进行卷积处理。为了扩大感受野、提取更加有效的特征信息,第一层卷积层采用了较宽的卷积核;而在池化层则采用了 全局平均池化(Global Average Pooling)。该池化操作对卷积层提取的特征进行重采样,并提取其全局信息,随后引入到注意力通道中。

在注意力层中,使用共享的 多层感知机(Multi-Layer Perceptron,MLP) 实现特征变换和信息重组,之后传递至全连接层(Fully Connected Layer, FC)并接入 Sigmoid 激活函数。最后,增强后的特征被输入到 双向门控循环单元(BiGRU) 层,用于时间序列预测。
CNN 网络由若干卷积层、池化层和全连接层构成,具备强大的特征提取能力(图 3b)。CNN 的核心操作是 卷积算子,它能融合局部感受野内的空间信息和通道信息以构建具有判别性的特征。卷积层采用不同大小的卷积核,有效提取输入特征图中的局部关键特征;池化层则对特征图进行压缩,降低维度并简化网络计算复杂度;最终,全连接层将所有特征进行整合并传递至分类器输出。
BiGRU(双向 GRU) 是一种双向循环神经网络,它在原始 GRU 模型的基础上引入了反向传播机制,即同时包含正向 GRU 与反向 GRU 两层(图 3c)。一层处理输入序列的正向信息,另一层则处理反向信息,最后将两层的输出进行融合,从而生成最终输出结果。这一结构增强了模型在时间序列双向特征提取方面的能力,使其能够捕捉当前数据与过去及未来的关联关系。
GRU 本身包含两个门控单元:重置门(reset gate) 和 更新门(update gate)。在任意时间步 t t t,GRU 神经元接受两个输入:前一时刻的隐藏状态 h t − 1 h_{t-1} ht−1 与当前输入 x t x_t xt,并输出当前隐藏状态 h t h_t ht。与 LSTM 相比,GRU 将遗忘门和输入门合并为一个更新门,从而简化了结构。重置门控制当前输入与前一隐藏状态的结合程度,其计算依赖于 Sigmoid 激活函数:
z t = σ ( W z ⋅ [ h t − 1 , x t ] + b z ) r t = σ ( W r ⋅ [ h t − 1 , x t ] + b r ) h ~ t = tanh ( W ⋅ [ r t ⋅ h t − 1 , x t ] + b ) h t = ( 1 − z t ) ⋅ h t − 1 + z t ⋅ h ~ t (6) \begin{aligned} z_t &= \sigma(W_z \cdot [h_{t-1}, x_t] + b_z) \\ r_t &= \sigma(W_r \cdot [h_{t-1}, x_t] + b_r) \\ \tilde{h}_t &= \tanh(W \cdot [r_t \cdot h_{t-1}, x_t] + b) \\ h_t &= (1 - z_t) \cdot h_{t-1} + z_t \cdot \tilde{h}_t \end{aligned} \tag{6} ztrth~tht=σ(Wz⋅[ht−1,xt]+bz)=σ(Wr⋅[ht−1,xt]+br)=tanh(W⋅[rt⋅ht−1,xt]+b)=(1−zt)⋅ht−1+zt⋅h~t(6)
其中:
- z t z_t zt 为更新门;
- r t r_t rt 为重置门;
- h ~ t \tilde{h}_t h~t 为候选隐藏状态;
- h t h_t ht 为当前隐藏状态;
- W W W 和 b b b 分别为权重矩阵与偏置项。
3.4 精度评价与对比
为了验证所提出方法的性能,本文开展了对比实验,分别使用 CNN-BiGRU、BiGRU 以及 BiLSTM 模型对滑坡运动进行预测。
为更有效地展示本文方法的优势,首先采用 经典的 K-means 聚类算法,基于变形幅度将所有散射点进行分类。聚类数目的确定基于 肘部法则(Elbow Method),即评估聚类内误差平方和随聚类数的变化趋势。
在每个聚类中,随机选取若干散射点,对其预测位移时间序列进行建模,并与其他模型的预测结果进行比较。详细分析与对比结果见 结果与讨论 章节。
在模型训练中,CNN-Attention-BiGRU 的具体参数设定如下(见表 1):

- CNN 的卷积通道数设为 32;
- 卷积核大小设为 [ 3 , 1 ] [3,1] [3,1];
- BiGRU 采用 Adam 优化算法;
- 最大迭代次数设为 300;
- 初始学习率为 0.01;
- 学习率衰减因子设为 0.5;
- 时间步长度为 6。
所有模型的训练与计算均在高性能工作站上完成,确保了高效的数据读写与计算性能。在效率方面,每个散射点的预测过程约需 8–10 分钟。
数据划分上,77% 的时间序列被用于训练,剩余部分用于模型验证。
为了进一步评估模型性能,采用 均方根误差(RMSE)、平均绝对误差(MAE) 和 决定系数( R 2 R^2 R2) 三项指标,其计算公式如下:
- 平均绝对误差:
MAE = 1 n ∑ t = 1 n ∣ y r ( t ) − y p ( t ) ∣ (7) \text{MAE} = \frac{1}{n} \sum_{t=1}^{n} \left| y_r(t) - y_p(t) \right| \tag{7} MAE=n1t=1∑n∣yr(t)−yp(t)∣(7)
- 均方根误差:
RMSE = 1 n ∑ t = 1 n ( y r ( t ) − y p ( t ) ) 2 (8) \text{RMSE} = \sqrt{ \frac{1}{n} \sum_{t=1}^{n} \left( y_r(t) - y_p(t) \right)^2 } \tag{8} RMSE=n1t=1∑n(yr(t)−yp(t))2(8)
- 决定系数:
R 2 = 1 − ∑ t = 1 n ( y r ( t ) − y p ( t ) ) 2 ∑ t = 1 n ( y r ( t ) − y ˉ r ) 2 (9) R^2 = 1 - \frac{\sum_{t=1}^{n} (y_r(t) - y_p(t))^2}{\sum_{t=1}^{n} (y_r(t) - \bar{y}_r)^2} \tag{9} R2=1−∑t=1n(yr(t)−yˉr)2∑t=1n(yr(t)−yp(t))2(9)
其中:
- y p ( t ) y_p(t) yp(t) 表示模型预测值;
- y r ( t ) y_r(t) yr(t) 表示实际位移值;
- y ˉ r \bar{y}_r yˉr 表示实际值的平均值;
- n n n 为样本数。
MAE 与 RMSE 是连续变量预测中最常用的评估指标,分别表示预测值与观测值之间的绝对误差和平方误差。 R 2 R^2 R2(决定系数)用于衡量回归模型的拟合优度,其取值范围为 [ − 1 , 1 ] [-1,1] [−1,1]:
- 当 R 2 = 1 R^2 = 1 R2=1 时,模型拟合完美,能够完全解释因变量的变化;
- 当 R 2 = 0 R^2 = 0 R2=0 时,模型拟合效果与使用因变量均值预测效果相同;
- 若 R 2 < 0 R^2 < 0 R2<0,则说明模型拟合效果甚至不如简单平均预测,可能由于模型结构与数据特征严重不匹配(如对非线性数据采用线性模型等)。
4. 结果分析
4.1 MT-InSAR 形变与环境配置
4.1.1 边坡不稳定性与诱发因素
图 4 展示了 2016 年 3 月至 2022 年 6 月期间基于 InSAR 技术获取的辛铺滑坡形变及其空间分布情况。滑坡形变量呈现出显著的空间异质性,中段及前缘处变形最为剧烈,后缘区域则相对较弱。其中前缘中部是变形最严重的区域,年均变形速率高达 − 52.16 mm/year -52.16 \ \text{mm/year} −52.16 mm/year。统计分析结果显示,在此期间辛铺滑坡的平均年变形速率为 − 13.07 mm/year -13.07 \ \text{mm/year} −13.07 mm/year。其中,62.89% 的点位变形速率介于 0 0 0 至 − 15 mm/year -15 \ \text{mm/year} −15 mm/year 之间,29.63% 位于 − 15 -15 −15 至 − 30 mm/year -30 \ \text{mm/year} −30 mm/year 之间,仅有 7.48% 的点位变形速率超过 − 30 mm/year -30 \ \text{mm/year} −30 mm/year(图 4b)。实地调查验证了 InSAR 监测结果的准确性:在滑坡前缘房屋内发现多条裂缝(图 4c–4d),而在前缘中部道路上则发现一条约 100 米长的裂缝(图 4e),与 InSAR 数据高度一致。

4.1.2 多个水文年的形变对比
水文年定义为连续 12 个月的周期,其划分原则是使储水变化最小化,从而最大程度地降低年际间水量差异(Nalbantis 和 Tsakiris, 2009)。我们统计分析了 2016–2021 年间的滑坡形变数据(图 5)。从结果来看,辛铺滑坡在各水文年内具有一致的形变空间分布,即变形强弱区域大致相似,但形变强度在不同年份之间存在明显差异。2017 年是形变最剧烈的一年,平均年变形速率为 − 17.64 mm/year -17.64 \ \text{mm/year} −17.64 mm/year,其中 17.07% 的 InSAR 点位年变形速率超过 − 30 mm/year -30 \ \text{mm/year} −30 mm/year,强变形区的范围也最大(图 5b)。
相比之下,2019 年的形变最为稳定,平均变形速率仅为 − 10.69 mm/year -10.69 \ \text{mm/year} −10.69 mm/year,其中 74.31% 的点位年变形速率低于 − 15 mm/year -15 \ \text{mm/year} −15 mm/year,超过 − 30 mm/year -30 \ \text{mm/year} −30 mm/year 的仅占 3.36%。在 2016、2018、2020 和 2021 年,滑坡前缘,尤其是中段,依然表现出显著变形,年变形速率分别为 − 12.06 -12.06 −12.06、 − 14.80 -14.80 −14.80、 − 15.54 -15.54 −15.54 和 − 16.49 mm/year -16.49 \ \text{mm/year} −16.49 mm/year。图 5g 展示了滑坡运动对应时期内的 12 天累计降雨量与 12 天平均库水位(RWL)变化曲线,其中 PS-2 点位形变最大。三峡水库水位的泄放与回蓄表现出相对一致且重复的规律。典型的“台阶状”位移模式揭示了滑坡的蓄水诱发特征,可能与孔隙水压力增加有关(Xia 等, 2024)。降雨数据显示出强烈的年际差异,2017 年和 2021 年降雨量显著高于其他年份,并与滑坡加速形变时段高度重合。可以看出,2019 年滑坡活动趋于稳定,2020 和 2021 年再次活跃。我们将在后续章节中对 2017 年进行更为详细的定量分析。

4.1.3 单一水文年(2017 年)内的统计比较
研究区的降雨与水位变化在一个水文年内具有明显的周期性特征(Xia 等, 2024;Zhou 等, 2022a)。多水文年形变对比分析表明,2017 年是滑坡活动最强的一年,因此我们选取 2017 年作为典型案例,展示单一水文年内的滑坡形变演化过程(图 6)。2017 年 1 月至 4 月,水位从 175 m 缓慢下降至 162 m,此阶段累计降雨量为 86 mm,日最大降雨量为 20 mm,滑坡处于缓慢变形或停滞状态。5–6 月,库水位快速下降至 145 m,叠加雨季初期的降雨过程(累计降雨量 357.5 mm,日最大降雨量 237.5 mm),导致滑坡前缘中部和左侧区域迅速启动,变形速率加快。7–8 月,水位持续维持低位并出现小幅波动,累计降雨量达 486.5 mm,最大日降雨量为 116 mm,前缘区域变形进一步加剧。9–10 月,随着三峡水库开始蓄水,水位逐渐上升,尽管此阶段降雨总量仍高(679.5 mm),但滑坡变形趋缓。11–12 月,水位回升至 175 m 并趋于稳定,降雨减少,滑坡进入稳定状态。

4.1.4 滑坡运动验证与分类
为进一步验证 InSAR 监测结果,我们将 InSAR 提取得到的位移时间序列与辛铺滑坡 GNSS 监测站获取的形变数据进行了对比。图 7 显示了 PS-1 点位与 GNSS 站 G15 的对比结果。GNSS 数据根据 Dai 等(2022)的方法,结合滑坡坡向与坡度信息,转换至雷达 LOS 方向。对比结果表明两者高度吻合,均方根误差(RMSE)约为 0.64 cm,平均绝对误差(MAE)约为 0.53 cm,显示出 InSAR 在形变监测方面的可靠性与精度可媲美高精度 GNSS 测量。为了进一步分析滑坡区域内部差异,我们基于变形幅度采用 K-means 聚类算法对所有散射点进行空间分类(图 7)。其中 Class 1(红色)为快速变形点,主要集中于滑坡前缘区域;Class 2 和 Class 3 分别代表中速与慢速变形点,主要分布在滑坡体内部和后缘区域。每一类中随机选取两个典型散射点,作为后续预测分析的代表点。

4.2 滑坡变形预测
4.2.1 位移时间序列的分解
在本研究中,我们采用了VMD(变分模态分解)模型对LOS(视线方向)上的总位移进行分解。该方法假设信号是由一系列子信号组成的,每个子信号具有特定的中心频率和有限的带宽,这些子信号被称为IMFs(本征模态函数)。由于所使用的Copernicus数字高程模型(DEM)的分辨率限制,我们未进行坡度方向转换。
VMD利用经典的维纳滤波思想,通过求解一个变分问题来获得这些IMF分量。该变分问题旨在识别信号在频域中的中心频率和带宽约束,从而有效地提取出每个中心频率所对应的有意义信号分量。通过在频域中分析非周期性信号,这种方法可以将复杂信号分解为多个谐波信号。
在对位移序列进行分解和重构之后,我们得到了趋势项与周期项,并分别对这两个分量进行了预测。VMD分解结果如图8所示。我们在图7所示的新浦滑坡区域中为每一类随机选取了两个散射点(PS点),以详细展示时间序列的预测过程。这些点的位置在图7中展示。

通过分解,可以简化复杂的时间序列,从而提升预测的准确性。该方法通过分离位移序列中的基本组成成分,实现了更精确的分析,最终提高了滑坡位移的预测能力。
4.2.2 趋势与季节性分量预测
采用 ARIMA 模型对 PS-1 至 PS-6 的趋势项位移进行预测,如图 9 所示。测试结果表明,所选 InSAR 监测点的趋势项测试集的所有 R 2 R^2 R2 值均超过 0.9,表明该模型在使用 ARIMA 方法准确预测趋势项位移方面的有效性。这个高 R 2 R^2 R2 值表示预测位移趋势与实际位移趋势之间存在强相关性,验证了趋势项预测的可靠性与精度。接下来,我们估算了 12 天、24 天和 36 天累积降雨量、12 天平均库水位(RWL)与这些五个因素变化与 InSAR 监测点 PS-1 和 PS-2 季节性项之间的相关性。此相关性通过灰色关联分析(GRA)进行验证,以检查这些诱发因子序列与滑坡位移变化之间的关系。

图 10 显示了 PS-1 和 PS-2 两个 InSAR 监测点的季节性项与五个因素之间的灰色关联性。总体来看,估算的灰色关联度均超过 0.7,揭示了降雨量和 RWL 对辛铺滑坡的显著影响。随后,使用 CNN-Attention-BiGRU 模型结合诱发因子序列预测散射点的季节性项。训练使用了 2016 年 3 月至 2020 年 12 月的 146 个位移数据,2021 年 1 月至 2022 年 6 月的 44 个数据作为测试集。结果如图 10 所示,突出了我们提出的模型在预测季节性位移方面的表现。通过与 CNN-BiGRU、BiGRU 和 BiLSTM 模型的对比实验,结果表明我们提出的方法在建模季节性项方面具有优越的表现。后续的讨论将进一步详细阐述这一点。

4.2.3 滑坡位移时间序列的组成
通过将滑坡位移趋势项与季节性项相加得到累积位移预测结果,如图 11 所示。对具有最大运动的 Class 1 中两个典型散射点 PS-1/2 进行预测,并与 CNN-BiGRU、BiGRU 和 BiLSTM 等常见预测模型进行比较。同时,展示了散射点的监测累积位移,作为标准值进行对比。从结果来看,我们的方法在预测滑坡运动学方面表现更好,尤其是在位移变化显著的时期,并进行了详细的统计比较。

图 12 展示了准确性统计和实验结果,表明本文提出的 CNN-Attention-BiGRU 模型在整体预测精度方面优于其他传统模型。该比较使用了辛铺滑坡中具有较大运动的 PS-1/2 散射点,这些散射点在之前的分类中被归类为 Class 1。对于 PS-1 点,我们提出的方法在 MAE、RMSE 和 R 2 R^2 R2 上的改善幅度分别为约 39% 至 56%、32% 至 55% 和 1% 至 5%,相比于 CNN-BiGRU、BiGRU 和 BiLSTM 模型。对于 PS-2 点,这些改善幅度分别为 MAE 约 23% 至 49%、RMSE 约 21% 至 50%、 R 2 R^2 R2 约 1% 至 4%。 R 2 R^2 R2 值表明所有模型表现良好,但我们的方法在预测滑坡运动学时更加稳定和精确,尤其是在显著位移变化期间,如图 11 所示。CNN 和注意力机制的结合有效降低了滑坡位移预测的误差,增强了其预测性能和能力。

4.2.4 我们方法的鲁棒性评估
为了进一步评估我们提出的方法的鲁棒性,我们使用相同的参数进行了额外的实验,即我们多次预测周期性分量和总滑坡运动学,每个选定的散射点从 PS-1 到 PS-6 进行了 10 次实验。结果如图 13 和图 14 所示。结果表明,预测的滑坡运动学并非总是恒定的;相反,它们在一个接近真实位移的范围内变化。
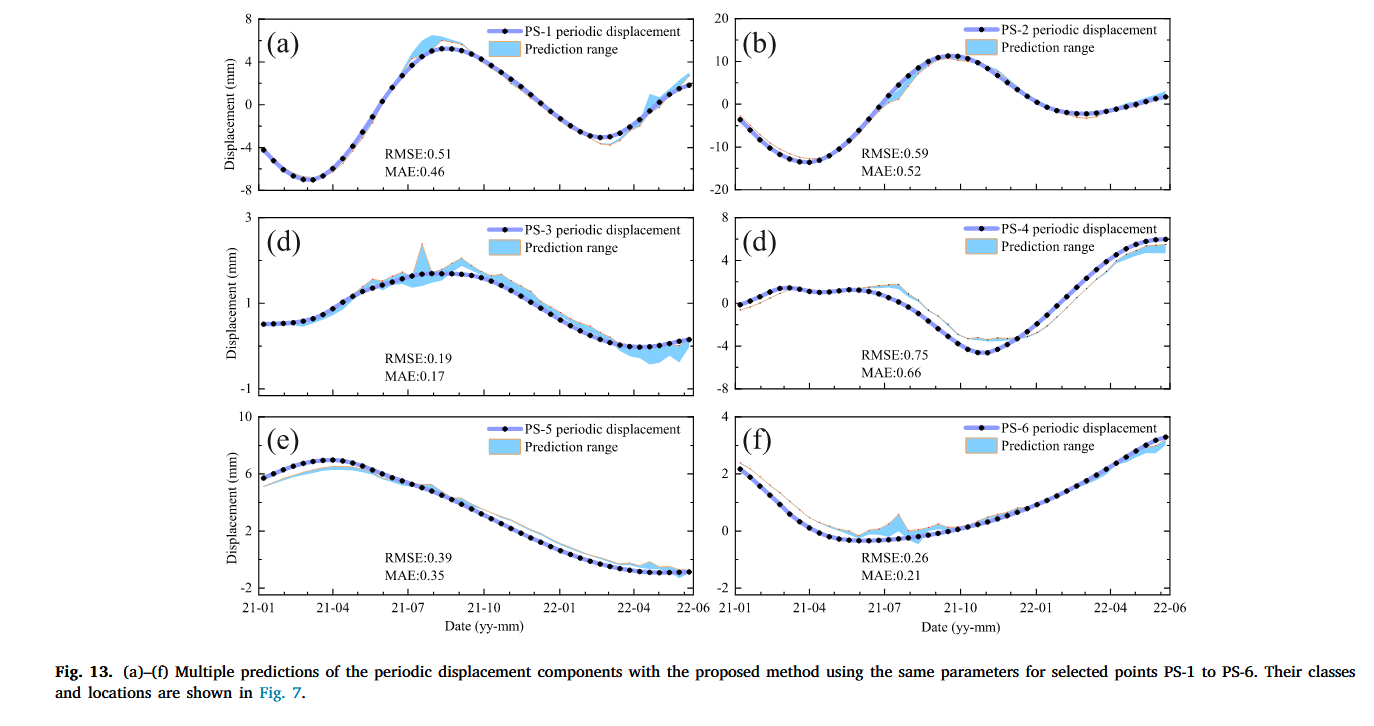

因此,预测的周期性变形分量的 RMSE 和 MAE 值分别在 0.19–0.75 和 0.17–0.66 mm 之间。而对于预测的累积位移,RMSE 和 MAE 范围分别为 0.16–2.46 和 0.14–2.07 mm。显然,Class 1 中具有较大运动的散射点 PS-1/2 的预测误差比其他点更大。此外,PS-3 的预测在所有选定散射点中最为准确。与大多数先前在深度学习和时间序列分析中的研究不同,这些研究通常在将时间序列分解后才将其分为训练和测试数据集(Liu 等, 2024;Song 等, 2024;Wang 等, 2023, 2022),这种方法可能会影响预测结果的客观性。
为此,我们进行了额外的实验,进一步评估了分解策略的影响,即我们通过仅将 VMD 技术应用于训练数据来修改我们的方法论,而将剩余的时间序列保持不变,以便直接预测后续的运动。结果如图15所示,表明这种调整后的策略仍能有效捕捉运动特征,尽管与之前策略的结果相比误差略大。尽管存在这些误差,整体结果的幅度仍然相当接近,预测覆盖的范围也更广。整体 MAE 和 RMSE 分别约为 4.0 和 4.8 mm。这个修订后的策略与深度学习中的时间序列预测标准实践一致,提供了更好的客观性,同时保持了可接受的精度。尽管精度略逊一筹,但这种方法可能更适用于地质灾害预测等地质学深度学习实际应用中。该实验的结果可能为遥感领域提供有价值的见解,尤其是增强复杂环境中预测深度学习模型的可靠性。

5. 讨论
5.1 地质特性与触发因素
XinPu滑坡体以第四纪松散沉积物为主,土壤为含有砾石的粉质粘土,提供了丰富的滑坡物质。以往研究发现,该地区容易发生渗流驱动的滑坡,滑坡体内渗透性差,降雨和 RWL 变化也是影响滑坡发生的关键因素(Xia 等, 2024;Zhou 等, 2022a;Lacroix 等, 2020;Tomás 等, 2016)。降水增加可通过提高水分含量降低土壤的抗剪强度,增强滑动体的渗流过程。土壤强度的软化和孔隙水压力的增加,进一步降低了坡体稳定性。在暴雨过程中,水迅速通过松散的土壤结构渗透到隔水层中,大量水分积聚导致滑动带土壤软化。至于 RWL 波动,当 RWL 快速下降时,滑坡体内的地下水不易渗出,从而在地下水位和 RWL 之间形成水头差。由此产生的外向渗流力可能导致滑坡滑动力的增加。
5.2 基于机器学习的变形预测
在本研究中,我们选择了 VMD 方法进行时间序列分解。尽管还有其他方法,如独立成分分析(ICA)(Peng 等, 2022)和傅里叶变换(Singh 等, 2017),VMD 具有独特的优势,使其特别适合我们的应用,即 VMD 生成的模型函数具有清晰的物理可解释性,增强了信号分析和理解(Rehman 和 Aftab, 2019)。作为一种非递归的变分分解方法,VMD 有效地缓解了经常影响经验模态分解(EMD)的模态混叠问题。与 ICA 或主成分分析(PCA)不同,后者通常需要预设独立成分或主成分的数量,VMD 能根据信号特征自适应确定模型函数的数量。与假定常频率成分的傅里叶变换不同,VMD 可以通过解决变分模型处理非线性/非平稳数据。这些优势使得 VMD 在我们分解需求中尤其有效。
在滑坡位移预测中,并非所有的时间特征都具有相同的重要性;通常,快速位移变化期间的特征比稳定期的特征更为关键。总体目标是生成 CNN-Attention 卷积层输出的通道注意力权重,这可以增强重要通道的特征表示,帮助推导与季节性项相关的注意力权重映射结果。因此,可以进行并实现可解释性的分析。注意力机制的本质是为不同特征分配权重,从而突出它们的重要性。由于 CNN 无法捕捉时间序列信息的双向连接,我们结合了注意力机制,以进一步基于 CNN 网络提取时间特征。CNN-Attention 层通过首先将输入特征序列与一维卷积核进行卷积,形成矩阵。然后,对该卷积输出进行全局平均池化,生成一个新的特征向量,表示每个通道对特征提取的影响。该全局池化向量随后通过共享的多层感知机(MLP)获得通道权重。这些权重通过 Sigmoid 函数激活,生成最终的注意力权重矩阵,反映每个通道的重要性。然后,这个注意力矩阵与原始输入时间序列矩阵进行加权相乘,以增强输入特征。通过这种 CNN-Attention 层处理过程,重要特征被放大,而不重要的特征则被抑制,从而提高了对相关信息的响应。使用机器学习模型进行滑坡变形预测已成为岩土工程和遥感领域的重要进展(Tehrani 等, 2022;Zhou 等, 2022a;Zhang 等, 2021a)。
5.3 CNN-Attention模型特征权重的特点
大多数使用深度学习进行滑坡位移预测的模型通常被认为是“黑箱”模型,缺乏可解释性。这些模型的低可解释性导致滑坡预测模型存在可靠性差、高数据依赖性以及模型调优和参数调整困难等问题。为了解决这些问题,我们的研究将注意力权重融入CNN-Attention模块,以增强模型的可解释性和透明性。如图16所示,我们通过生成注意力热图来揭示CNN-Attention模型在预测滑坡运动学时特征权重的特点。输入特征包括降水量、RWL和历史滑坡位移。时间戳t表示当前时刻的三个数据集的特征权重,而时间戳t−1表示前一个时间点的特征权重,类似于时间戳t−n。横轴表示输入数据的时间戳,纵轴表示该时间戳与历史时刻之间的延迟。这些权重表示输入序列中每个时间戳在预测滑坡位移时的相对重要性。权重越大,说明该时间戳及其对应的影响因素的相对重要性越大。

位于xinpu滑坡体前缘的散射点PS-1和PS-2,受降水量和RWL波动的显著影响。这两个点被选中进行进一步的注意力权重分析,以阐明触发因素与滑坡变形模式之间的动态相互作用。对于PS-1和PS-2这两个具有快速运动的点,我们观察到从4月到8月期间注意力权重大,恰好与RWL大幅下降和降水量增加的时段重合,这两个因素是滑坡活动的主要驱动因素。随着7月之后环境条件的稳定,这些权重随之上升和下降,突显了RWL和降水波动对变形动态的影响。我们的研究还分析了每个时间戳前六个历史时刻,以评估历史因素对当前滑坡位移的影响。结果证实,触发因素的历史时刻对当前滑坡位移有影响,这表明滑坡位移预测涉及复杂的时间序列分析,而不仅仅是简单的回归分析。CNN-Attention机制有效捕捉了这种潜在的关联,为理解滑坡变形的时序动态提供了更深入的洞察,并增强了深度学习模型的可解释性。这一理解对于全面分析滑坡行为至关重要。类似的方法也可以应用于其他滑坡案例,通过深度学习预测位移时间序列,更好地揭示建模过程中的触发因素的重要性。
6. 结论
本研究通过基于MT-InSAR观测数据的深度学习方法解决了滑坡位移预测的复杂问题,提出了一种具有可解释性的预测模型。为了提高预测的准确性和可解释性,我们提出了一种耦合CNN-Attention-BiGRU模型,并将其应用于新浦地区的滑坡位移预测。CNN模型中的卷积和池化操作有效地学习了多变量因素的特征,而通道注意力机制增强了时间特征的提取。随后,BiGRU模型利用历史信息实现了更准确的滑坡位移预测。实验结果表明,我们提出的模型在与其他方法的比较中表现更好,具有更高的系数,证明其在滑坡位移预测中的可靠性。
CNN-Attention机制提供的可解释结果表明,触发因素与滑坡变形之间的动态关系可以被突出显示,并且在4月至8月期间,位移迅速变化区域的散射点所受的影响因素具有较高的相对重要性。这一时期恰逢RWL和降水量的显著波动,表明这些因素对快速滑坡位移有重要影响。此外,该机制还揭示了历史影响因素,如过去的降水量和RWL,也对当前的位移有显著影响,突显了历史数据和当前数据之间的时间关联。
总体而言,我们的方法在预测滑坡运动时具有良好的迁移性、可解释性和稳健性,优于传统的预测方法,并且可应用于其他类似的灾害案例,具有广泛的深度学习多学科灾害风险减缓应用前景。
