【算法】双指针8道速通(C++)
1. 移动零

思路:
拿示例1的数据来举例,定义两个指针,cur和dest,cur表示当前遍历的元素,dest以及之前表示非零元素

先用cur去找非零元素,每找到一个非零元素,就让dest的下一个元素与之交换
单个交换流程

在过程中,可以将整个数组划分成三个区域

总流程:

至此就让非零元素在不改变顺序的前提下移到前面了
代码实现:
void moveZeroes(vector<int>& nums)
{for(int dest=-1,cur=0;cur<nums.size();cur++)//dest以及以前的元素是非零元素,cur以及以后的是当前遍历元素{if(!nums[cur])//如果该位置是0,就继续找非零元素{continue;}else//否则就把非零元素交换到dest位置{dest++;int tmp = nums[dest];nums[dest] = nums[cur];nums[cur] = tmp;}}
}2. 复写零

思路:
先来简单说一下暴力解法

不过这都是双指针专题了,当然还是要以双指针解法为主
这次我们定义两个指针,一个是当前遍历的元素,一个是已经处理完的元素

但可以发现到这里时,原本的2被覆盖成0了,导致结果出错,所以这么从前往后遍历是不行的
那从后往前呢?
我们先假设知道最终结果

那对于这组数据来说,最后就只会遍历到4
也就是cur遍历到4时,dest就已经到最后了(当cur是非零元素时候,dest加一,当cur是零元素时,dest加2,所以只要数据中有0,dest就会比cur更快到达终点),

再靠现在的数据从后往前遍历(当cur为非零元素时,将arr[dest]的数据改成arr[cur],并且让cur和dest都往前走一步;当cur为零元素时,将arr[dest]和arr[dest-1]的数据都改成0,并且让cur往前走一步,dest往前走两步)

那么怎么才能让cur停止到最后一个元素的位置呢?
我们可以先让cur和dest从头走一遍,但只是单纯的走一遍,不要写入数据,否则就会把没遍历的数据复写掉,如图所示

当dest大于等于最后一个元素位置时,就退出,这样cur就停在复写零之后的最后一个位置了
但是这样的话有一种特殊情况会出错

可以看到,当复写零完之后的最后一个元素是0时,dest会加两次,从而导致它超出了数据的范围,到了数据范围之外的下一个位置,这样再从后往前复写时,首先就会访问到非法的数据导致出错,所以,当检测到dest==arr.size()时,应先完成这一次的复写操作,避免以后出错
if(dest==arr.size())
{dest--;//让dest不会非法访问arr[dest--]=0;//复写操作之后再让dest-1,这样后面才可以正常的从后往前复写cur--;//该位置已经复写完毕,所以--
}代码实现:
void duplicateZeros(vector<int>& arr)
{int cur = 0,dest = -1;while(1){if(!arr[cur])//如果该元素是零dest+=2;//让dest向后移动两位else//如果不是零dest++;//就向后移动一位if(dest >= arr.size()-1)//如果dest已经到底了,就跳出break;cur++;//如果还没到底,就继续判断(这里把cur写在判断的下面,可以防止cur最后多加一位)}if(dest==arr.size())//如果dest最后在数组以外的下一个元素位置,就代表最后一次加了两次,那最后一个数就是0{dest--;arr[dest]=0;//但我们这里只需要弄一个0就行(因为第2个0在数组外面)cur--;dest--;}while(cur>=0)//从右往左覆盖,就不用担心覆盖了还没读的数据了{if(!arr[cur])//如果该元素是0,就覆盖两次{arr[dest--]=0;arr[dest--]=0;cur--;}else//否则覆盖一次{arr[dest--]=arr[cur--];}}
}3. 快乐数

思路:
先来看题目的示例2,把它的运算轨迹写下来就是这样

那这组数有什么规律呢?

从第二次4出现时,后面的轨迹就完全重复了
所以我们可以把它简写成这样

这不就是一个环形链表吗?没错,那4就是入环的值
那示例1可以不可以写成环形链表的形式呢?

1的各个位数的平方和还是1,所以对于快乐数而言,它的环就都是1
如果对环形链表不熟悉,可以看我的这篇文章
力扣题目分享:LCR 022.环形链表II(C语言)
为什么我这么能确认它一定是一个循环?而不是像无理数那样的无限不循环?
因为题目中说了,如果不会变为1,就是无限循环的数据
那如果它不是无限循环的数据,我们还有没有别的办法使得避免陷入死循环?

如图所示,即使题目没有说必定会是循环,我们也可以通过计算推出来一个快乐数最多只会运行811次平方和
先来模拟一下示例一(是快乐数)的轨迹

那不是快乐数的轨迹是怎么样的呢?下面来模拟一下示例二

代码实现:
int LL(int n)//返回一个数的每个位置上的数字的平方和
{int sum = 0;while(n){sum+=(n%10)*(n%10);n/=10;}return sum;
}
bool isHappy(int n)
{int fast = n,slow = n;//快慢指针,快指针走两次,慢指针走一次while(1)//照题目的意思(无限循环),即终究会重复(和环形链表的思想相似){fast = LL(fast);//快指针走两步fast = LL(fast);//fast = LL(LL(fast));//这样也可以slow = LL(slow);//,慢指针走一步if(fast == slow)//如果他们相遇了{if(fast == 1)//并且相遇的位置的值是1return true;//就代表是快乐数elsereturn false;//否则就不是}}
}4.盛最多水的容器

思路:
如果是暴力解法的话,相信大家都能写出来,无非是两层for循环嵌套,但这样是过不了的,因为O(N^2)太大了
拿示例一来举例,定义两个变量,left和right,分别指向当前数组中最左边和最右边的值

那现在如果拿height[left]和height[right]充作左边和右边的长,那这个容器最大能盛的水的高度就是较小的那一边(木桶效应),宽就是left和right之间的距离
算完之后,left和right应该如何移动呢?
如果让right向左移动会发生什么?

此时容器的高度是多少呢?好像还是上一次的height[left],但宽度相比上次要少了1,那整体的容量就是减小了,也就是说,不管想左移后的right的值变没变大,整体容量都会减少,那right的值如果变小了,容量就会减的更多了
所以,第一次的容量就是固定住left的前提下能盛的最大的容量
因此,要让较小的那一边继续往中间靠拢(这样还有可能增加容量)
也就是这样

那算完这次之后应该移动哪边呢?
因为height[right]的值较小,所以要让right--
也就是这样

不断往复,直到left>=right
看一下模拟过程

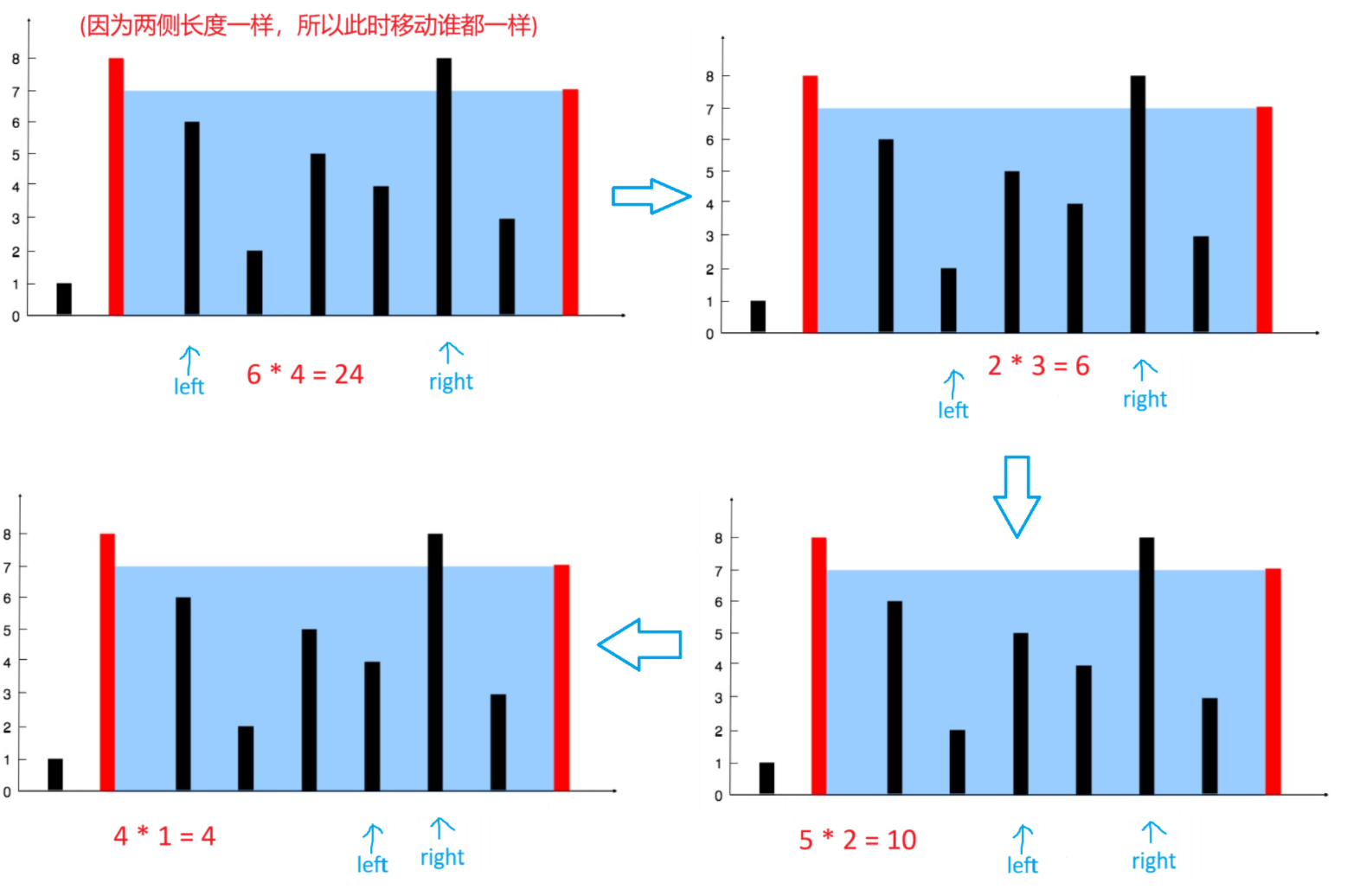

代码实现:
int maxArea(vector<int>& height)
{int left = 0,right = height.size()-1;int Max = 0;//这是目前最大的盛水量while(left<right){Max = max(min(height[left],height[right])*(right-left),Max);//最大盛水量是取的当前盛水量和Max的较大值if(height[left] < height[right])//如果左边的长较小,那右边的长无论怎么往左移,盛水量都只会缩小,所以当前盛水量就是固定左边长的情况下最大的盛水量了left++;//所以要让左边的长往右移else//那如果右边的长较小,也一样right--;//所以要让右边的长往左移}return Max;
}5.有效三角形的个数

思路:
先复习一下判断三角形的条件:有三条边a,b,c,有a+b>c && a+c>b && b+c>a时,就可以判断这三条边可以构成三角形,但其实还有个更简单的方法
若a <= b <= c,那只需要a+b>c就可以判断这三条边可以构成三角形,因为a和b是最小的两条边,最小的两条边相加都大于最大的那条边了,那其他两条边相加肯定也会大于第三边
这也是这道题的核心思想:即在a <= b <= c的前提下,a+b>c就可以判断它是三角形
那我们就需要给这个数组定义三个指针,分别代表三条边的a,b,c,但怎么才能知道哪个数大哪个数小呢?
所以还需要先排序
排序后,最大的数就在最后了
c从后往前遍历,也就是让每个最大的数都当一遍c,然后right在max的前一个,left在第一个

为什么要这么排呢?对于当前数组来说,nums[left]+nums[right] >nums[max],所以2,3,4可以组成三角形,那既然2,3,4可以,那left+1后的的2,3,4也肯定可以(因为left一开始是在0的位置,越往后越大,最小的left都可以组成三角形了,那其他比它大的数也肯定可以了),所以这一次计算就得出了两种三角形
那下一步是移动left还是right?
上面我说过了,这一次只要能组成三角形,那left的值是(left,right-1)时的情况都成立,所以此时再让left++就没有意义了,因此要让right--

这种情况组成不了三角形,因此要让left++,去寻找更大的两条边来试
但再加left<right的条件就不成立了
所以这时max--

让right再等于max-1,left再等于0,重新上面的步骤
代码实现:
int triangleNumber(vector<int>& nums)
{//核心:在a<=b<=c情况下,a+b>c就可以证明是三角形sort(nums.begin(),nums.end());//先排序int max = nums.size()-1;//让从后往前来,即让最大的那个数当cint cnt = 0;for(;max>=2;max--){int left = 0,right = max - 1;//这是比c小的数的区间while(left < right){if(nums[left] + nums[right] > nums[max])//如果a+b>c,那a后面的数+b也一定>c{cnt += right - left;//加上a后面的数的次数right--;//[]+b>c的情况已经加完了,然后换一个b}else{left++;//既然a+b<=c,那a前面的数也肯定<=c了,所以换个a}}}return cnt;
}6. 查找总价值为目标值的两个商品(原:和为s的两个数字)

思路:
先简单讲一下人人都会第一时间想到的暴力解法,在这道题来说也就是暴力枚举
拿示例2来举例

就是把全部的情况都试一遍,直到相加==target
但这样的时间复杂度是O(N^2),太大了,过不了
这时就要用到本篇主打的算法了——双指针
定义两个变量left和right,分别指向数组的第一个和最后一个元素

此时的和要大于target,那现在是要移动left还是移动right呢?
既然left现在是最小的值,那最小的值和right相加都大于target,如果让再移动,那left所指向的值不更大了吗?

所以现在要让right--

现在的和小于target了,那此时right再向左移动的话,值只会更小,所以接下来要让left++

因为现在的和大于target,所以此时要让right--

此时的和等于target,跳出
代码实现:
vector<int> twoSum(vector<int>& price, int target)
{int left = 0,right = price.size()-1;//分别指向数组的第一个和最后一个while(left<right){if(price[left] + price[right] > target)//如果现在的和要比目标值要大,就要减小值,所以right--right--;else if(price[left] + price[right] < target)//如果要小,就要增大值,所以left++left++;else//如果找到了,就返回这俩数return {price[left],price[right]};}return {0,0};//照顾编译器
}7.三数之和:

思路:
这道题的暴力解法无非就是三重for循环,找到全部符合条件的元祖之后再用set去重,但它的时间复杂度太高了,还是直接引入本篇的主题——双指针 吧
这道题其实可以优化成上一道题(和为s的两个数字)来解,nums[i] + nums[j] + nums[k] == 0,即nums[i] + nums[j] == -nums[k],这不就是上一个题的解法吗?

排好序之后,定义三个变量,i,left,right,分别代表上述的nums[k],nums[i],nums[j],让当left和right指向的值相加等于-nums[i]时,就是一种结果
现在就来模拟一下示例1的过程

此时,结果小于-nums[i],按照上一题的解法,就让left++以此让两者相加的值更接近-nums[i]

此时left还是-1,不管是否成立,都会重复结果,这时候就需要去重操作
因为此时的数组已经排好序了,相同的元素都挨在一起,我们可以让这三个指针在移动时直接跳过重复的元素
对于上图的案例来说,第一个-1判断完后,就应该直接让left移动到0处

中途就不断重复这样的过程,直到找到第一组案例

此时虽然是找到了一组案例,但仔细看这组案例[-1,-1,2],里面有重复的元素,是不合法的,所以去重的条件应该设为nums[i] != nums[i+1](left和right也同样适用)

所以当i从-1开始时,left应该从0开始才对
此时大于-nums[i] ,就让right--,以缩小它们两个的和

此时终于找到了第一组合法的案例
这时要让left和right都++并且确保nums[left]和nums[right] != nums[left-1] 并且 != nums[right-1]
当left>=right时就需要再次移动i并且确定新的left和right了
以此类推,直到i +2 >= nums.size()时,i后面就不足两个元素了,此时就不用看了
小优化:
如果三个数相加起来的和的0的话,那它们三个起码会有一个负数,那么,当i>0时,三个数就必然是正数了,此时就没有必要排序了,所以只需要遍历到i>0为止
代码实现:
vector<vector<int>> threeSum(vector<int>& nums)
{sort(nums.begin(),nums.end());//先排序int i=0,left,right;//当nums[left] + nums[right] == -nums[i]时,他们仨相加就为0了vector<vector<int>> vv;while(i+2<nums.size())//如果i到了nums.size()-1或者-2的地方,就凑不够三个数了{while(i>0 && nums[i] == nums[i-1] && i+2<nums.size())//因为重复的元组不要,所以遍历时直接忽略重复的元素i++;int target = -nums[i];//让nums[left]+nums[right]==targetleft = i+1,right = nums.size()-1;//[left,right]就是[i+1,nums.size()-1]的区间范围while(left < right)//开始从区间内寻找==target的两个元素{if(nums[left] + nums[right] > target)//如果>target,就要缩小他们两个相加的结果,所以要让right--{right--;while(nums[right] == nums[right+1] && left < right)//因为重复的元组不要,所以遍历时直接忽略重复的元素right--;}else if(nums[left] + nums[right] < target)//如果<target,就要增大他们两个相加的结果,所以要让left++{left++;while(nums[left] == nums[left-1] && left < right)//因为重复的元组不要,所以遍历时直接忽略重复的元素left++;}else//此时nums[left]+nums[right]==target,即nums[left]+nums[right]+nums[i]==0{vector<int> v;vv.push_back({nums[i],nums[left],nums[right]});//初始化列表可以构造一个临时的vector//将left和right都往中靠齐一样right--;while(nums[right] == nums[right+1] && left < right)//因为重复的元组不要,所以遍历时直接忽略重复的元素right--;left++;while(nums[left] == nums[left-1] && left < right)//因为重复的元组不要,所以遍历时直接忽略重复的元素left++;}}i++;}return vv;
}8. 四数之和:

思路:
这道题和上一道题可以说是师出同门,用暴力解法也就是四重循环找元组,不过既然师出同门,那当然也就意味着同样可以和上一题一样用双指针解法
我们可以先把这道题优化成三数之和
即定义一个target1 = target - nums[a],这样只要满足nums[b] + nums[c] + nums[d] == target1 即可
然后三数之和问题又可以优化成第6题两数之和
即定义一个target2 = target1 - nums[b],这样只要满足nums[c] + nums[d] == target2即可
当然,在进行这些操作前,都要先排序
拿示例1来演示

如图所示,红色方框是一个三数之和,而三数之和里面的棕色方框就是两数之和
当然,还有去重操作,在四数之和也同样需要
即这四个变量在移动时要确保下一个元素和上一个元素不相同
代码实现:
vector<vector<int>> fourSum(vector<int>& nums, int target)
{sort(nums.begin(),nums.end());//先排序vector<vector<int>> vv;int a,b,left,right;a=0;//第一个数,从左往右开始遍历while(a+3 < nums.size())//如果到了nums.size()-3的位置,a后面就不足3个数了,就不可能找到了{//taget1和taget2设成long long 是为了防止数据溢出long long target1 = target - nums[a];//再以target1为目标解决三数之和问题b = a + 1;//b从[a+1,nums.size()-1]遍历while(b+2 < nums.size())//如果到了nums.size()-2的位置,b后面就不足2个数了,就不可能找到了{long long target2 = target1 - nums[b];//两数之和问题left = b+1,right = nums.size()-1;//在[b+1,nums.size()-1]区间内找两数之和 == target2的元祖while(left<right){if(nums[left] + nums[right] > target2)//如果过大,就要缩小相加的和,所以right--{right--;while(left<right && nums[right] == nums[right+1])//去重操作(为了避免下一个要加的被操作数和现在的一致)right--;}else if(nums[left] + nums[right] < target2)//如果过小,就要增加相加的和,所以left++{left++;while(left<right && nums[left] == nums[left-1])//去重操作(为了避免下一个要加的被操作数和现在的一致)left++;}else{vv.push_back({nums[a],nums[b],nums[left],nums[right]});//用初始化列表插入一个vectorleft++;//找到一个元祖之后,要让left和right都++while(left<right && nums[left] == nums[left-1])//去重操作(为了避免下一个要加的被操作数和现在的一致)left++;right--;while(left<right && nums[right] == nums[right+1])//去重操作(为了避免下一个要加的被操作数和现在的一致)right--;}}b++;while(b+2 < nums.size() && nums[b] == nums[b-1])//去重操作(为了避免下一个要加的被操作数和现在的一致)b++;}a++;while(a+3 < nums.size() && nums[a] == nums[a-1])//去重操作(为了避免下一个要加的被操作数和现在的一致)a++;}return vv;
}