考研系列-计算机组成原理第二章:数据的表示和运算
一、数制与编码
(一)重点知识



(二)习题总结
2.1.5习题总结








二、运算方法和运算电路
(一)重点知识
2.2.1基本运算部件








2.2.2定点数的移位运算
1.算数移位

2.移位操作总结

2.2.3定点数的加减运算

2.2.4定点数的乘除运算
1.原码一位乘法


2.补码一位乘法(Booth算法)

手算过程

3.原码的除法
(1)手算二进制除法

(2)原码除法-恢复余数法
硬件细节
ACC值和MQ值会逻辑左移,以达到做减法后补零的效果。
ACC内存储的是被除数、余数(作为下一次除操作的被除数)

手算过程

(3)原码除法-不恢复余数法(加减交替法)
加减交替法是对恢复余数法的改进,把恢复余数的过程改进为“逻辑左移+除数”的操作


这里要求被除数比除数要小,否则在第一步的被除数减余数的过程中就会检测出来
4.补码的除法-加减交替法


2.2.5.C语言里的类型转换
注:在C语言中定点整数是用“补码”存储的

2.2.6.数据的存储和排列
(1) 数据存储的“大端方式”和“小端方式”
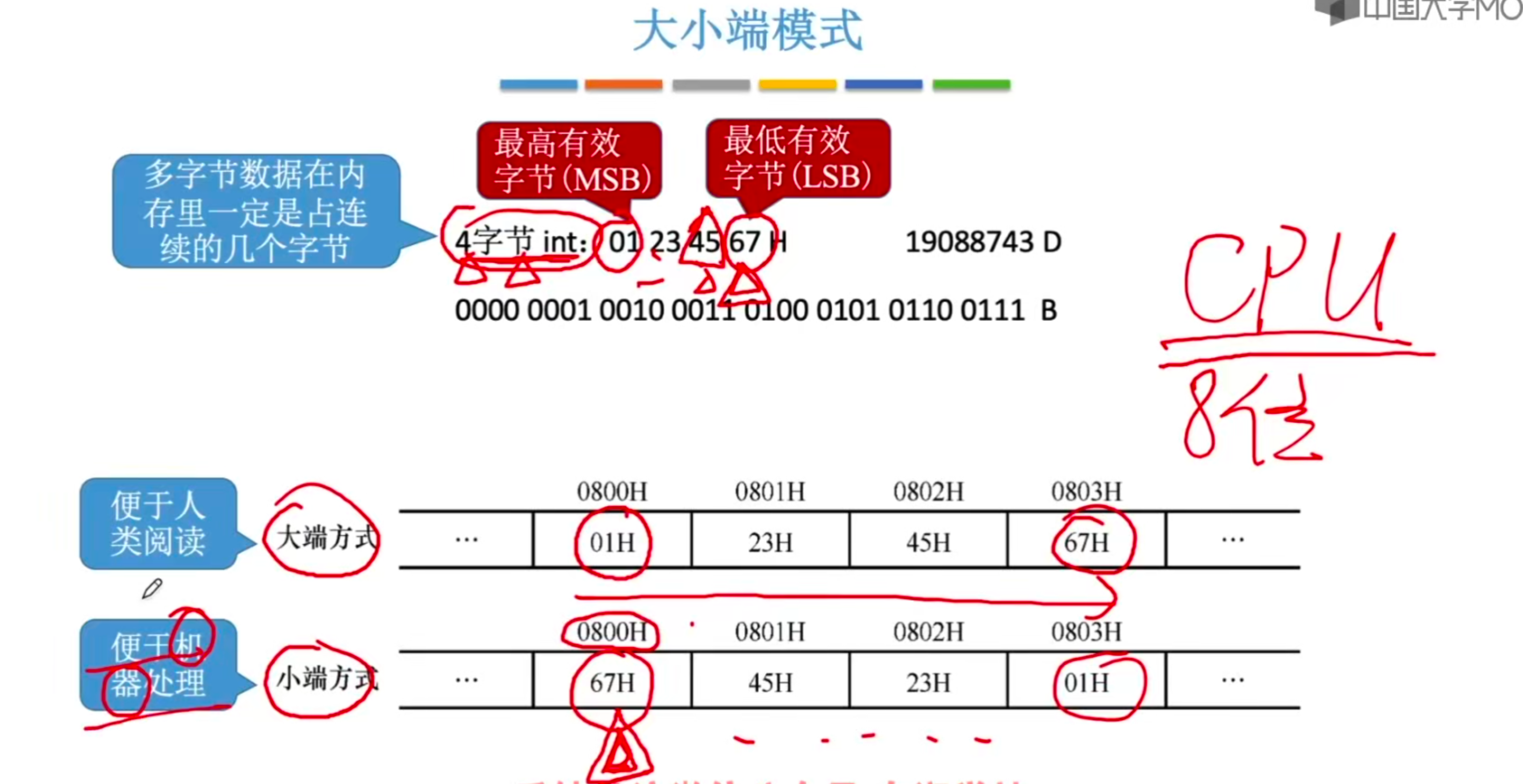
(2) 边界对齐

(二)习题总结
序号代表在书中的题号
选择题
4.并行进位加法器
进位产生函数、进位生成信号(本地进位):Gi=Ai Bi
进位传递函数(进位传递条件):Pi=Ai异或Bi
10.注意不带标志位的循环移位,移出来的数还需要放到标识位处
15.模4补码:

A.模4补码与模2补码不同,模4补码包含了模2补码的所有优点,并且更容易检测判断加减运算中的溢出问题(而不是乘除问题)
B.模4补码存储时只需要一个符号位。(正确)
D.模4补码在算数与逻辑部件(ALU)中需要两个符号位
18.溢出的判别方法:P40
(1)采用一位符号位
(2)采用双符号位
初始时正数符号位为00;负数符号位为11
(3)采用一位符号位——根据符号位的进位Cs和最高数位数的C1异或表示,结果为0表示无溢出;结果为1表示溢出。
20.原码乘法是先取操作数绝对值相乘,符号位单独处理。原码的一位乘法中,符号位不参与运算。
26.补码除法:补码不恢复余数除法中,异号相除时,够减商0,不够减商1。

27.关于移位:

A.假设机器数采用反码表示,当机器数为负时,左移时最高数位丢0,结果出错,右移时最低位丢0,影响精度。如5位反码:10010
B.在算数移位的情况下,补码左移的前提条件是其原最高有效位与最高符号位相同。可以举例子
C.在算数移位的情况下,双符号位的移位操作只有低符号位需要参与移位操作。双符号位的最高符号位代表真正的符号,而低位的用于参与移位操作以判断是否发生溢出,如01表示结果正溢出,如果是10表示结果负溢出。
29.加法器的两个输入信息和输入的低位进位信息:

注意如果是做减法,第二个要先取反码作为输入,低位进位sub传入1。
43.减法操作只需要判断借位标志,CF=1表示有借位,不够减。
习惯用双符号位计算溢出标志位。


简答题
1.有符号数在计算机中是以补码形式存在和运算的
![]()

7.程序涉及有符号整数加减、无符号整数加减运算,这四种运算能否利用一个加法器辅助电路实现,请简述理由:


三、浮点数的表示与运算
(一)重点知识
1.浮点数的表示

2.规格化



这里需要注意补码表示的尾数规格化时,符号位(最高位)需要和最高数值位(第二位)相反,也就是当符号位为负时,数值最高位需要精确到0(左移或右移实现,阶码做出相应的处理)。
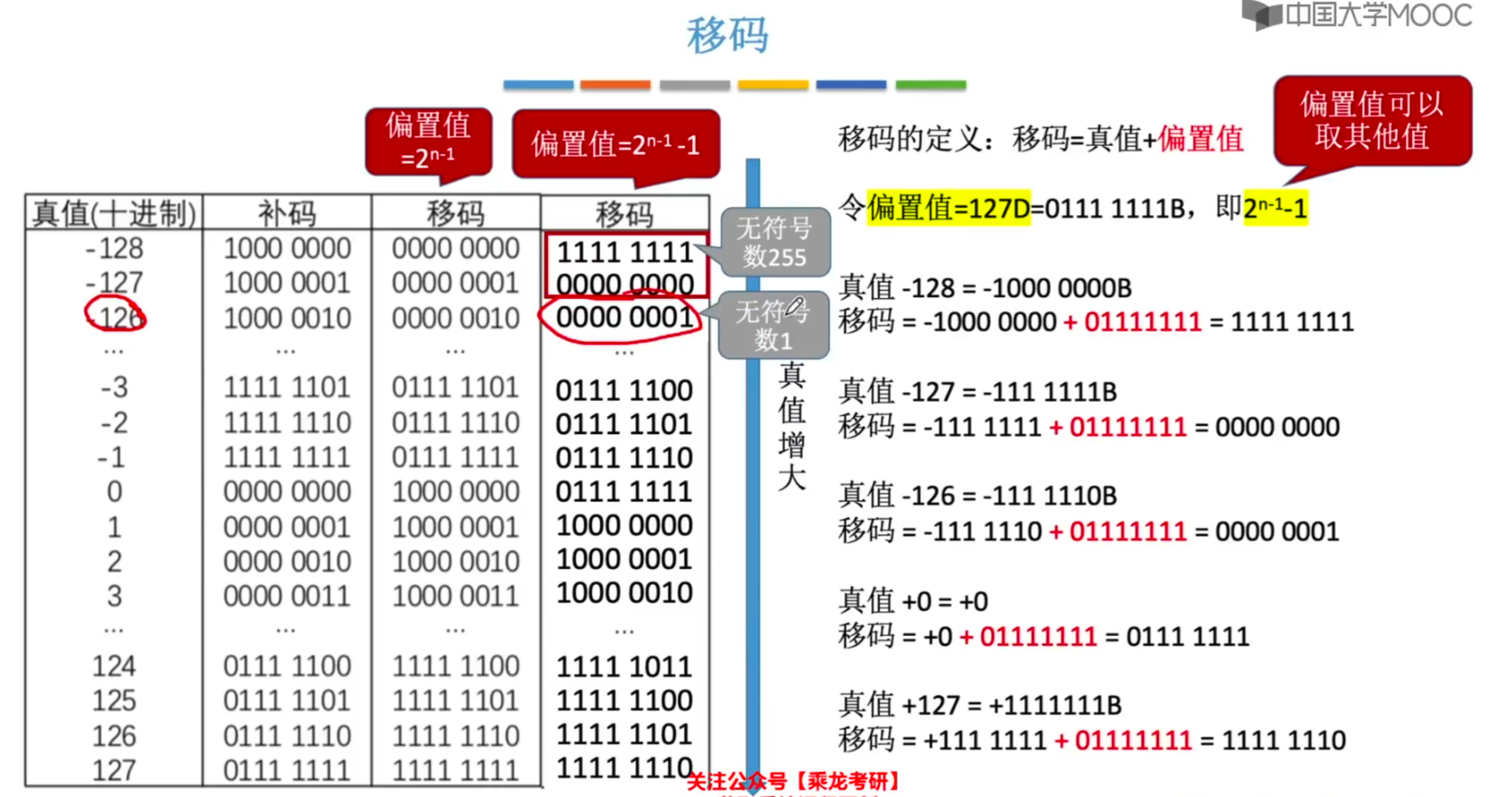
3.移码回顾


IEEE754的偏置值为127,区别于上述的常用的128
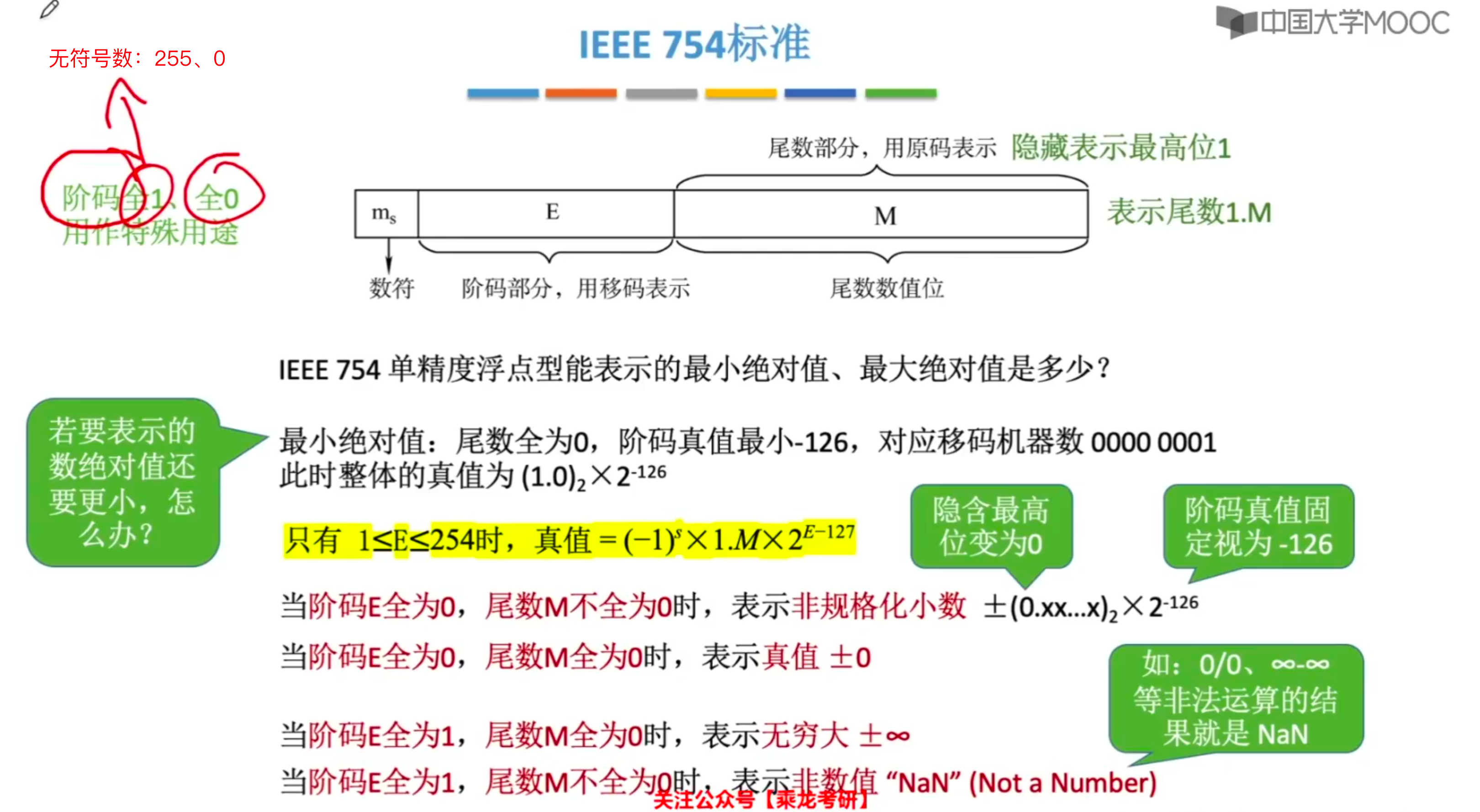
4.IEEE754标准

移码表示:阶码真值+偏移量
(1)十进制数转化为单精度浮点数的例子

(2)单精度浮点数转化为十进制数的例子

(3)规格化数的表示范围

(4)阶码为特殊值时表达的含义
5.浮点数的加减运算


6.强制类型转换


(二)习题总结
序号代表在书中的题号
选择题
3.长度相同、格式相同的两种浮点数,假设前者基数大,后者基数小,其他规定均相同,则它们可表示的数的范围和精度为:前者可表示的数的范围大但精度低(数变稀疏)。
(1)基数越大,在运算中尾数右移的可能性越小,运算的精度损失越小
(2)由于基数大时发生因对阶或尾数溢出需要右移时及规格化需要左移的次数显著减少,因此运算速度可以提高
(3)基数越大,可表示的数的范围越大
5.在规格化浮点运算中,若某浮点数为25*1.10101,其中尾数为补码表示,则该数:需要将尾数左移一位规格化(注意是尾数左移,区别于小数点左移,别混了)。
这里注意:尾数为补码时,正数规格化形式为0.1xxxxxx,负数的规格化形式为1.0xxxxxxxx,详情2.3.2
6.规格化浮点数中:
这里注意:尾数为原码时,正数规格化形式为0.1xxxxx,负数规格化形式为1.1xxxxxx。(数值最高位都是1)
7.在浮点加减运算对阶操作中,如果阶码增加,则尾数右移。(对阶操作中阶码不会缩小,所以也不会有相应的尾数左移)

注意,尾数的最高数位都省略了一个1。
13.采用规格化浮点数的最主要目的是:增加数据的表示精度。

14.关于几种说法:
(1).在计算机中,表示的数有时候会发生溢出,根本原因是计算机的字长有限。
(2).8421码不是二进制数,而是十进制数。
(3).正数的补码、反码、原码都一样
(4).设有正的规格化浮点数N1=2m*M1和N2=2n*M2,若m>n,则有N1>N2。
21.对于舍入的说法
(1)浮点数可能需要舍入,定点数没有舍入的情况
(2)在浮点数舍入中,只有对阶、右规格化时可能需要舍入
(3)舍入不一定会产生误差,如向下舍入11.00到11.0时是没有误差的
23.关于数据类型之间的转换


简答题
1.什么是浮点数的溢出?什么情况下发生上溢出,什么情况下发生下溢出?

5.错题(2):负数按照图示格式写出-27/64的规格化浮点数

这个题目好好注意,尾数用补码表示,负数小数变补码和整数变化一样,注意变化。
6.两个规格数进行加减法运算,最后对结果规格化时,能否确定需要右归的次数?能否需要确定左归的次数?

9.IEEE754标准浮点数的阶码为特殊形式时代表的含义:

四、本章总结





注意:
1.移码的概念,作阶码
2.双符号位补码加减计算,注意溢出判断
3.IEEE754单精度/双精度浮点数表示法,规格化、上溢出
