理解欧拉公式

1. 欧拉公式中的符号

• 欧拉公式
  $$e^{ix}=\cos x+i\sin x$$
• 当 $x=\pi$时
  $$e^{i\pi }+1=0//欧拉恒等式$$
  • $e$:自然对数的底
  • $i$:虚数，$i^2=-1$
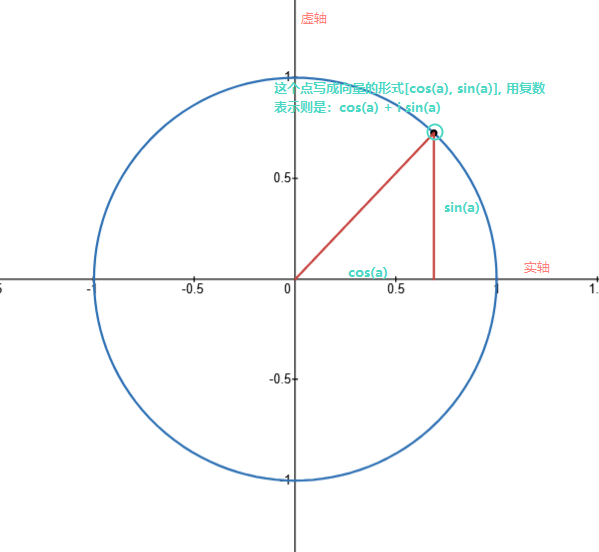
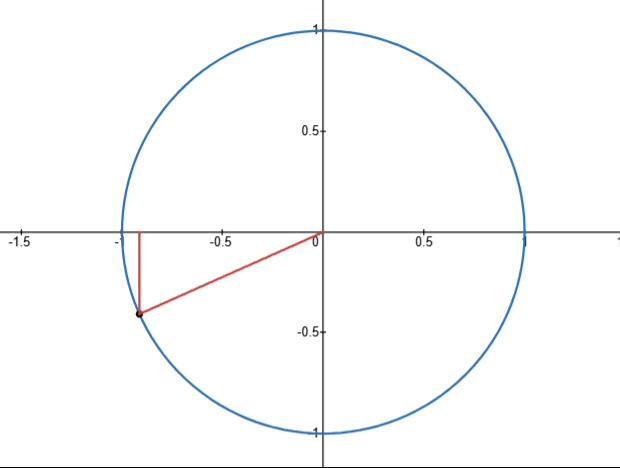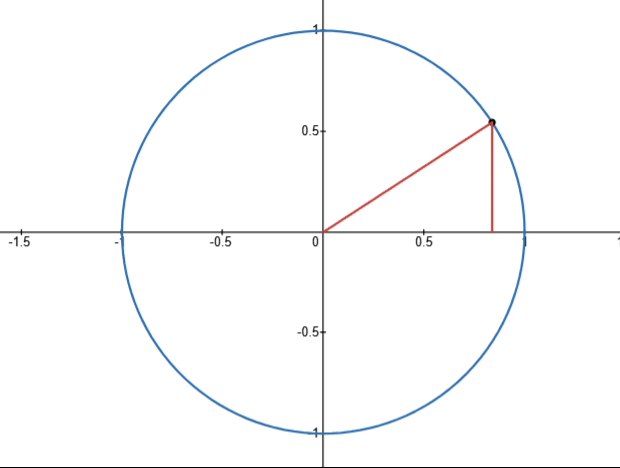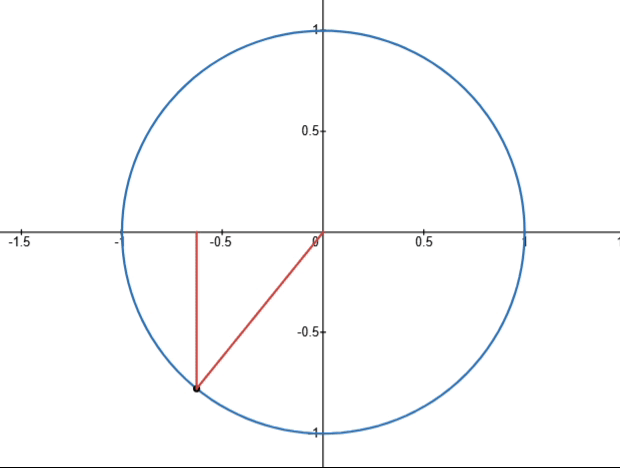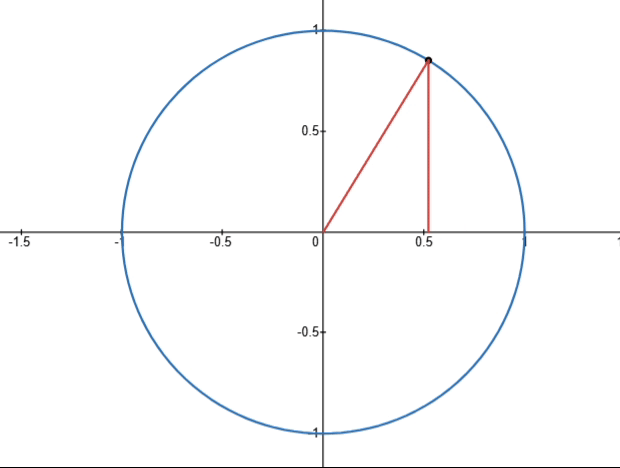
  • $\cos x+i\sin x$:复数，$\cos x$为实部，$\sin x$为虚部，实部和虚部对应复平面的一个点，在复平面中如下图所示(所有的点都落在一个单位圆上)：
• 
• 

2. 理解欧拉公式的左右两边为什么是相等的

2.1 自然对数的底 $e$ 是什么

• $e$ 表示 $n$ 趋近于无穷大时 $(1+\frac{1}{n}{)}^n$ 的极限，约等于 $2.718281828459045$
  $$e=\underset{n\to \infty }{\lim }{\left(1+\frac{1}{n}\right)}^n$$
• 记住一点：无论对$e^x$求几阶导，结果都为$e^x$,它的变化率是等于它本身的，它变化率的变化率也本身，变化率的变化率的变化率也等于它本身。。。。。。。可以无限套娃下去

2.2 $e^{ix}$ 为什么等于$\cos x+i\sin x$

• 方法是对左右两边分别进行泰勒展开，关于泰勒展开可以参考我的另外一篇文章《泰勒多项式》

• 对 $e^{ix}$ 在$0$点处进行泰勒展开：
  $$\begin{gathered} 泰勒公式 \\ {P}_n(x)=f(a)+f^{\prime }(a)(x-a)+f^{\prime \prime }(a)\frac{(x-a{)}^2}{2!}+...+f^{(n)}(a)\frac{(x-a{)}^n}{n!} \\ ------------ \\ 在零点处展开的公式（麦克劳林公式） \\ {P}_n(x)=f(0)+f^{\prime }(0)(x)+f^{\prime \prime }(0)\frac{(x{)}^2}{2!}+...+f^{(n)}(0)\frac{(x{)}^n}{n!} \\ ------------ \\ 将e^{ix}带入麦克劳林公式 \\ {e}^x=e^0+(e^0{)}^{\prime }(ix)+(e^0{)}^{\prime \prime }\frac{(ix{)}^2}{2!}+...+(e^0{)}^{(n)}\frac{(ix{)}^n}{n!} \\ ------------ \\ {e}^0的导数=e^0=1 \\ {e}^{ix}=1+ix+\frac{(ix{)}^2}{2!}+\frac{(ix{)}^3}{3!}...+\frac{(ix{)}^n}{n!} \\ ------------ \\ {e}^{ix}=\sum _{n=0}^{\infty }\frac{(ix{)}^n}{n!}//注：0!=1 \\ ------------ \\ 因为i^2=-1,所以在n为偶数的时候，i是可以消掉的，所以，上述公式也可以写成实部和虚部两部分 \\ {e}^{ix}=\sum _{n=0}^{\infty }\frac{(ix{)}^{2n}}{(2n)!}+\sum _{n=0}^{\infty }\frac{(ix{)}^{2n+1}}{(2n+1)!} \\ -- \\ {e}^{ix}=\sum _{n=0}^{\infty }(-1{)}^n\frac{x^{2n}}{(2n)!}+i\sum _{n=0}^{\infty }(-1{)}^n\frac{x^{2n+1}}{(2n+1)!} \end{gathered}$$

• 对$\cos x+i\sin x$进行泰勒展开

  • 对 $\cos x$ 进行泰勒展开，过程不过多赘述了，直接写结果
    $$\begin{gathered} \cos x=\cos (x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots . \\ \cos x=\sum _{n=0}^{\infty }{\left(-1\right)}^n\frac{x^{2n}}{(2n)!} \end{gathered}$$
  • 对 $\sin x$ 进行泰勒展开，过程不过多赘述了，直接写结果
    $$\begin{gathered} \sin (x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots . \\ \sin (x)=\sum _{n=0}^{\infty }{\left(-1\right)}^n\frac{x^{2n+1}}{(2n+1)!} \end{gathered}$$
  • $\cos x+i\sin x$ 的泰勒展开为
    $$\cos x+i\sin x=\sum _{n=0}^{\infty }(-1{)}^n\frac{x^{2n}}{(2n)!}+i\sum _{n=0}^{\infty }(-1{)}^n\frac{x^{2n+1}}{(2n+1)!}$$

• 总结：
  如下图所示 $e^{ix}=\cos x+i\sin x$ 的泰勒展开是完全一样的，所以等式两边是等价的
  

3. $e^{i\pi }+1=0$又为什么成立

3.1 分析

• $e^{i\pi }$中的 $\pi$ 代表的是什么？直接说答案 - 角度，准确的说是 $180^0$，这是弧度值的表示方法
• 使用弧度制如何表示一个角度呢？其实很简单，就是 弧长 / 半径$$\theta \left(\text{弧度}\right)=\frac{\text{弧长}s}{\text{半径}r}$$
• 半圆的弧长是$\pi r$， 所以$$180^0=\frac{\pi r}{r}=\pi$$
• 常见角度与弧度对照表​：

角度（度）	弧度（rad）
0°	0
30°	$\frac{\pi }{6}$
45°	$\frac{\pi }{4}$
60°	$\frac{\pi }{3}$
90°	$\frac{\pi }{2}$
180°	$\pi$

3.2 结论

• 因为 $\pi =180^o$,所以
  $$\begin{gathered} e^{i\pi }=\cos 180^o+i\sin 180^o \\ {e}^{i\pi }=-1+i\ast 0 \\ {e}^{i\pi }=-1 \\ ---------------------------------------------- \\ {e}^{i\pi }+1=0 \end{gathered}$$