【每天一个知识点】熵(Entropy)
“熵(Entropy)”是信息论、热力学、机器学习等多个领域的核心概念。它可以用一句话概括为:
🔑 熵表示系统的不确定性或信息混乱程度。
📚 一、信息论中的熵(Information Entropy)
在 Claude Shannon 的信息论中,熵衡量的是消息来源的平均信息量,也可视为我们从一个系统中获得的信息的不确定性。
📐 数学定义(离散情形)
设一个离散随机变量 XX 的概率分布为 p(x)p(x),则其熵定义为:

-
单位是 bit(比特)
-
如果某事件越不确定(概率越小),它的信息量越大
-
如果所有事件概率一致(最混乱),熵最大
🌰 举个例子:
-
抛一个公平的硬币:

-
如果硬币总是正面,熵为 0(完全确定)
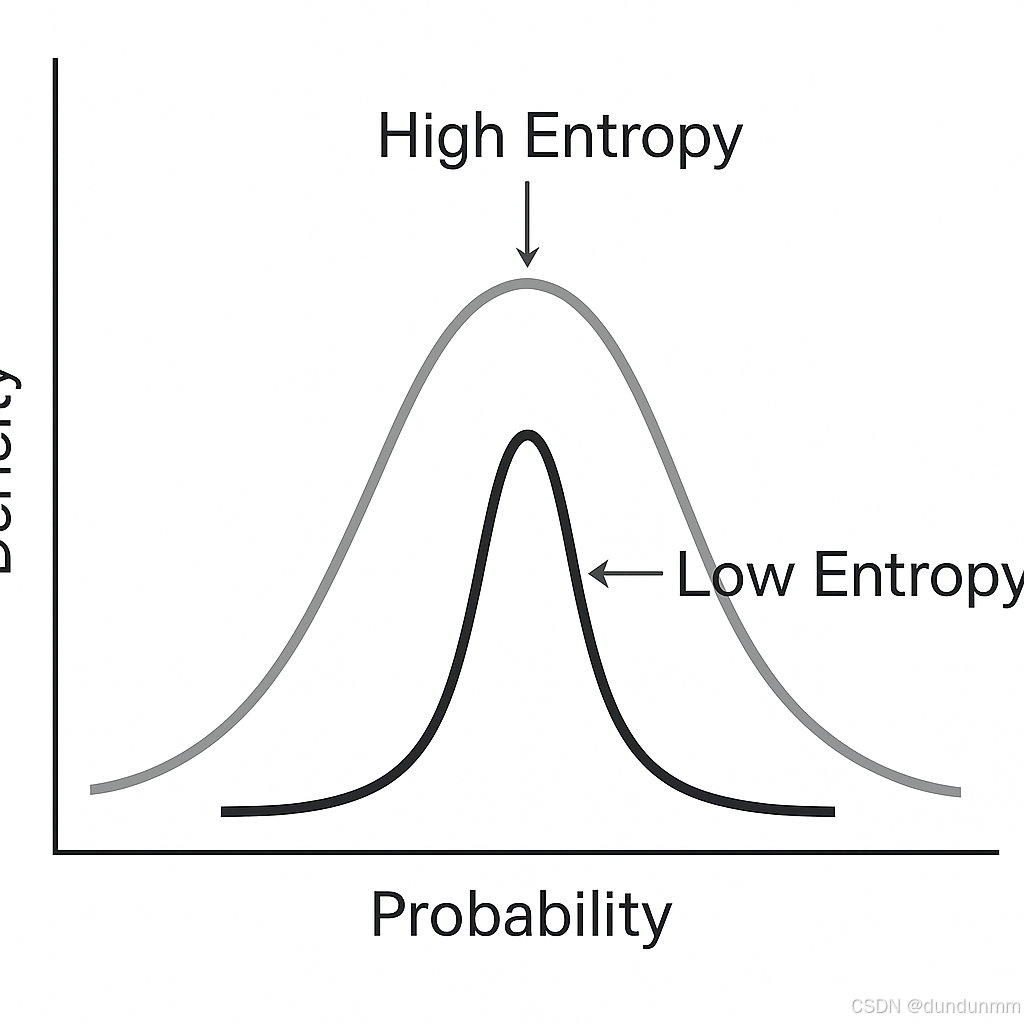
🔍 二、熵的图解理解
想象你要猜一个盒子里藏的是哪种球:
-
如果盒子中是 50% 红球 + 50% 蓝球 → 熵高,难猜
-
如果是 100% 红球 → 熵低,容易猜
📊 三、机器学习中的熵应用
1. 决策树中的信息增益(Information Gain)
-
熵用来衡量特征对数据分类的不确定性减少程度
-
决策树(如 ID3、C4.5)使用“熵下降”来选择分裂特征
2. 聚类/聚合中的熵损失
-
在聚类或分类时,类别越“纯”,熵越小
-
可用于聚类质量评估、联合聚类中的信息一致性判断
3. 表征多样性、熵正则化
-
在深度学习中,用熵来鼓励输出分布多样性(如GAN中的判别器)
-
熵小:模型过度自信;熵大:模型不确定性强
🔁 四、与其他概念对比
| 概念 | 定义 | 与熵的关系 |
|---|---|---|
| 信息量(Information Content) | I(x)=−logp(x)I(x) = -\log p(x) | 熵是信息量的期望 |
| 交叉熵(Cross Entropy) | 比较两个分布的平均编码代价 | 包含熵 + KL散度 |
| KL散度(相对熵) | 度量两个分布的差异 | 是熵差的一部分 |
🧠 五、直观理解
| 场景 | 熵高还是低? |
|---|---|
| 完全随机的骰子 | 熵高(最大) |
| 只出某一个点的骰子 | 熵低(最小) |
| 80% 是某一个结果 | 熵中等偏低 |