人工智能与机器学习:Python从零实现性回归模型
🧠 向所有学习者致敬!
“学习不是装满一桶水,而是点燃一把火。” —— 叶芝
我的博客主页: https://lizheng.blog.csdn.net
🌐 欢迎点击加入AI人工智能社区!
🚀 让我们一起努力,共创AI未来! 🚀
前言
在 AI 的热潮中,很容易忽视那些让它得以实现的基础数学和技术。作为一名专业人士,通过不使用机器学习库(比如 sklearn、TensorFlow、PyTorch 等)来编写模型,可以显著提升你对这些基础技术的理解。因为有时候,用现成的工具就像吃别人嚼过的糖,没劲!自己动手,那才叫真本事,不仅能搞懂背后的原理,还能在朋友面前炫耀一番:“看我这代码,多牛!”所以,咱们这就开始,一起踏上这个充满挑战和乐趣的旅程吧!🚀
本系列我们会深入探讨各种机器学习模型,并从零搭建它们。在每篇文章结束时,我希望读者能够对这些我们每天作为数据专业人士使用的模型有极其深入和基础的理解。咱们就从多元线性回归开始吧!
多元线性回归
多元线性回归可以用来模拟两个或多个自变量与一个数值型因变量之间的关系。日常用例包括根据房屋的卧室数量、浴室数量、面积等信息预测房价。咱们先来聊聊多元线性回归的一些关键假设。
- 自变量与因变量的线性关系:具体来说,任何一个自变量(或特征)变化 1 个单位时,因变量应该以恒定的速率变化。
- 没有多重共线性:这意味着特征之间需要相互独立。以房价为例,如果卧室数量和浴室数量之间存在某种相关性,这可能会影响模型的性能。确保没有或最小化多重共线性,也能让你更高效地利用给定的数据。
- 同方差性:这意味着在任何自变量水平下,误差都是恒定的。如果咱们的房价预测模型显示,随着预测价格的上升,误差也在增加,那咱们就不能说这个模型满足同方差性了。可能需要对特征数据进行一些变换,以满足这个假设。
数学原理
还记得 (y = mx + b) 吗?大多数人在公立学校的时候都学过这个公式。而多元线性回归则可以用下面的公式表示:
y = B 0 + B 1 x 1 + B 2 x 2 + ⋯ + B n x n + E y = B_0 + B_1x_1 + B_2x_2 + \dots + B_nx_n + E y=B0+B1x1+B2x2+⋯+Bnxn+E
图由作者通过 LaTeX Markdown 提供
- (y):因变量或目标变量,也就是咱们要预测的东西。
- (B_0, B_1, \dots, B_n):“Beta” 或自变量的系数。(B_0) 是截距,类似于 (y = mx + b) 中的 (b)。剩下的系数分别代表剩下的自变量或特征的系数。
- (x_1, x_2, \dots, x_n):自变量或特征。
- (E):“Epsilon”,更实际地说是误差项,也就是咱们的预测值与实际 (y) 之间的差距。
你也可以用矩阵表示法来表示多元线性回归方程。我个人更喜欢这种方法,因为它让我不得不从向量和矩阵的角度去思考,而这些正是几乎所有机器学习模型背后的数学核心。
Y = X B + E \mathbf{Y} = \mathbf{X} \mathbf{B} + \mathbf{E} Y=XB+E
图由作者通过 LaTeX Markdown 提供
咱们来更直观地看看这些变量里都有啥。先从 (\mathbf{X}) 开始,它代表了咱们所有的特征数据,是一个矩阵。注意,这个矩阵的第一列全是 1。为啥呢?这代表了截距项 (B_0) 的占位符。
从数据角度来看,咱们有啥呢?咱们有所有的特征数据、目标变量 (Y),误差项理论上是未知的,但它只是预测值 (y) 与实际值 (y) 之间的差距。换句话说,它只是用来补全方程的。所以,咱们需要求解的是 (\mathbf{B}),也就是权重。

图由作者提供
最小化代价函数
要找到 (\mathbf{B}),请注意,咱们并不是直接求解它。相反,咱们想找到向量 (\mathbf{B}) 中的值,使得预测值与实际值之间的误差最小化。这是通过最小化关于 (\mathbf{B}) 的代价函数来实现的,这个代价函数也被称为均方误差。
MSE = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 MSE=n1i=1∑n(yi−y^i)2
图由作者通过 LaTeX Markdown 提供
那怎么找到一个函数的最小值呢?求导并把导数设为 0。在这个例子中,咱们会执行这些步骤,然后求解 (\mathbf{B})。以下是逐步推导:展开代价函数、求导、把导数设为 0 来最小化函数,最后重新排列求解 (\mathbf{B})。
展开代价函数
B = ( X T X ) − 1 X T Y \mathbf{B} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{Y} B=(XTX)−1XTY
图由作者通过 LaTeX Markdown 提供
MSE = 1 n ( Y − X B ) T ( Y − X B ) \text{MSE} = \frac{1}{n} (\mathbf{Y} - \mathbf{X} \mathbf{B})^T (\mathbf{Y} - \mathbf{X} \mathbf{B}) MSE=n1(Y−XB)T(Y−XB)
图由作者通过 LaTeX Markdown 提供
对 (\mathbf{B}) 求导
∂ MSE ∂ B = − 2 n X T ( Y − X B ) \frac{\partial \text{MSE}}{\partial \mathbf{B}} = -\frac{2}{n} \mathbf{X}^T (\mathbf{Y} - \mathbf{X} \mathbf{B}) ∂B∂MSE=−n2XT(Y−XB)
图由作者通过 LaTeX Markdown 提供
最小化函数,即导数设为 0
− 2 n X T ( Y − X B ) = 0 -\frac{2}{n} \mathbf{X}^T (\mathbf{Y} - \mathbf{X} \mathbf{B}) = 0 −n2XT(Y−XB)=0
图由作者通过 LaTeX Markdown 提供
求解 (\mathbf{B})
B = ( X T X ) − 1 X T Y \mathbf{B} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{Y} B=(XTX)−1XTY
图由作者通过 LaTeX Markdown 提供
现在咱们已经搞懂了这个算法背后的数学原理,接下来就用 Python 来实现它吧!
我们的多元线性回归对象
正如前面提到的,咱们会在 Python 中实现它,而且不使用机器学习库。我超喜欢面向对象编程,所以咱们会搭建一个自己的多元线性回归对象。自己动手搭建这个对象的好处是,咱们可以随心所欲地添加功能。比如,我希望咱们的对象能方便地打印出评估指标,还能画出预测值与实际值的散点图。
咱们先从创建对象、导入需要的库(放心,我不会偷偷导入 sklearn 的),还有初始化函数开始。正如我前面提到的,我会搭建一个能自己进行训练集和测试集划分的多元线性回归对象。我希望这个对象能满足涉及这个算法的典型项目的所有需求,除了数据导入。
import pandas as pd
import numpy as np
import random
import matplotlib.pyplot as pltclass MultipleLinearRegression:def __init__(self):# 模型系数,初始值为 None,稍后会计算self.coefficients = None# 训练集特征数据self.X_train = None# 训练集目标数据self.y_train = None# 测试集特征数据self.X_test = None# 测试集目标数据self.y_test = None# 预测值self.y_pred = None
训练集/测试集划分方法
接下来,咱们添加第一个方法。这个方法和 sklearn 中的 train_test_split 长得很像。顾名思义,它会根据训练集的比例,把数据分成训练集和测试集。
def train_test_split(self, X, y, train_size=0.8, random_state=None):"""将数据划分为训练集和测试集。"""if random_state:np.random.seed(random_state)indices = np.arange(len(X))np.random.shuffle(indices)train_size = int(len(X) * train_size)train_indices = indices[:train_size]test_indices = indices[train_size:]self.X_train, self.X_test = X[X.index.isin(train_indices)], X[X.index.isin(test_indices)]self.y_train, self.y_test = y[y.index.isin(train_indices)], y[y.index.isin(test_indices)]
拟合方法
接下来的方法将是咱们对象中最复杂的部分。这里咱们会用训练数据来拟合模型。再次强调,咱们要解的是截距值和系数,这些都由向量 (\mathbf{B}) 表示。
B = ( X T X ) − 1 X T Y \mathbf{B} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{Y} B=(XTX)−1XTY
图由作者通过 LaTeX Markdown 提供
咱们一步步来。准备好学习 numpy 中的一些酷炫函数吧!记得,(\mathbf{X}) 是一个矩阵。目前,矩阵 (\mathbf{X}) 里只有特征数据。回想一下前面的内容,咱们需要一个全为 1 的列,作为截距系数 (B_0) 的占位符。这就是 np.ones() 和 np.hstack() 的用武之地。咱们需要这一列 1 的行数和特征数据的行数一样多。可以用矩阵 (\mathbf{X}) 的 shape() 方法轻松获取行数。第二个参数告诉 np.ones() 需要多少列 1。接下来,用 np.hstack() 把这一列 1 插入到矩阵 (\mathbf{X}) 的第一列。
跟上节奏了吗?现在该讲我认为这个项目中最复杂的代码行了。来看看咱们在解这个方程时必须执行的转置方法(用 (T) 表示)。当你转置一个矩阵时,第一行变成第一列,第二行变成第二列,以此类推。这也意味着一个形状为 2×3 的矩阵会变成一个形状为 3×2 的矩阵。下面是一个代码示例,直观展示这个过程:
import numpy as npa = np.array([[1,2,3],[4,5,6]])print(a,"\n")
print(a.T)

图由作者提供
接下来,咱们讲讲怎么进行矩阵乘法,也就是点积乘法。在 Python 中,特别是在 numpy 中,可以用 "@" 符号进行点积乘法。注意,这个符号经常被用作函数装饰器,但这超出了本文的范围。那两个矩阵怎么相乘呢?简单来说,可以定义为:将第一个矩阵的每一行的元素分别与第二个矩阵的每一列的元素相乘,然后求和。咱们可以用下面的函数来定义它。

定义只能帮你理解到这儿啦,咱们再看看 Python 里的另一个例子。假设你有两个矩阵,A 和 B,它们都是 2×2 的。如果咱们把这两个矩阵相乘,会得到下面这个矩阵,叫作矩阵 C。
import numpy as npa = np.array([[1,2],[3,4]])b = np.array([[5,6],[7,8]])c = (a @ b)
print(c)

咱们来回顾一下矩阵 C 中的每个值是怎么来的,按行依次来看。第一个值 19 在第一行第一列,计算过程如下:
[
(1 \times 5) + (2 \times 7)
]
更明确地说,咱们取矩阵 A 第一行的第一个元素,乘以矩阵 B 第一列的第一个元素。接着,取矩阵 A 第一行的第二个元素,乘以矩阵 B 第一列的第二个元素,把这两个乘积相加,就得到了 19。接下来,看看 43 是怎么来的:
[
(3 \times 5) + (4 \times 7)
]
花点时间琢磨琢磨这里咱们干了啥。咱们取矩阵 A 第二行的第一个元素,乘以矩阵 B 第二列的第一个元素,然后加上矩阵 A 第二行第二个元素与矩阵 B 第二列第二个元素的乘积。看出规律了吗?简单来说,就是第一个矩阵按行,第二个矩阵按列,这样一对一对地乘,再把结果加起来。记住,结果矩阵的行数应该和第一个矩阵的列数一样,而列数应该和第二个矩阵的行数一样。
别担心,咱们快把这部分拆解完了!接下来,咱们看看怎么用向量 Y 来乘矩阵,这在咱们要解的方程里是必须的。直接上 Python 代码示例。
import numpy as npa = np.array([[1,2,3],[4,5,6]])b = np.array([7,8,9])c = np.dot(a,b)
print(c)

图由作者提供
更明确地说,咱们取第一个矩阵的第一行的元素,分别乘以向量的每个元素,然后求和,就得到了 50。接着,对第二行也做同样的操作。回顾了两个矩阵相乘的过程后,这个就简单多了!
( 1 × 7 ) + ( 2 × 8 ) + ( 3 × 9 ) = 50 (1 \times 7) + (2 \times 8) + (3 \times 9) = 50 (1×7)+(2×8)+(3×9)=50
( 4 × 7 ) + ( 5 × 8 ) + ( 6 × 9 ) = 122 (4 \times 7) + (5 \times 8) + (6 \times 9) = 122 (4×7)+(5×8)+(6×9)=122
最后,咱们得看看怎么计算矩阵的逆。你可能会注意到,这部分咱们用了一个现成的公式。计算矩阵的逆是一个复杂的过程,但别担心,我还会给大伙儿讲讲背后的原理。
更具体地说,矩阵的逆可以用下面这个公式定义,其中 (\text{det}) 是矩阵 A 的行列式,(\text{adj}) 是矩阵 A 的伴随矩阵。伴随矩阵也可以描述为矩阵的余子式矩阵的转置。
A − 1 = 1 det ( A ) × adj ( A ) \mathbf{A}^{-1} = \frac{1}{\text{det}(\mathbf{A})} \times \text{adj}(\mathbf{A}) A−1=det(A)1×adj(A)
先从计算行列式开始。假设下面这个是矩阵 A:
A = [ a b c d e f g h i ] \mathbf{A} = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} A= adgbehcfi
行列式可以用下面这个公式计算:
det ( A ) = a ( e i − f h ) − b ( d i − f g ) + c ( d h − e g ) \text{det}(\mathbf{A}) = a(ei - fh) - b(di - fg) + c(dh - eg) det(A)=a(ei−fh)−b(di−fg)+c(dh−eg)
上面的公式可能看起来有点复杂,不过看看你能不能发现其中的规律。变量 (a, b,) 和 (c) 在第一行。注意变量之间的正负号?规律就是正、负、正、负,以此类推(可以认为变量 (a) 是第一个正号)。再看看括号里的内容?注意每组括号里的四个变量,它们在矩阵里既不共行也不共列。这些单独的变量组合代表了余子式矩阵。看看下面这个动图,从更实际的角度看看这个过程。
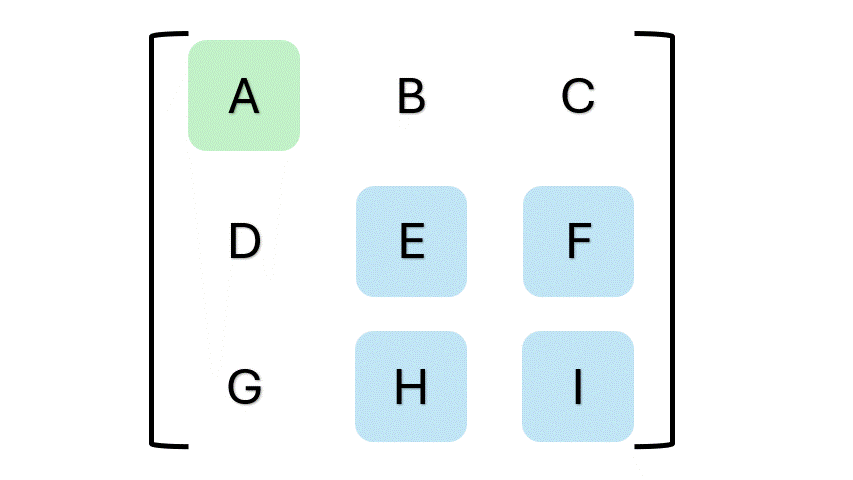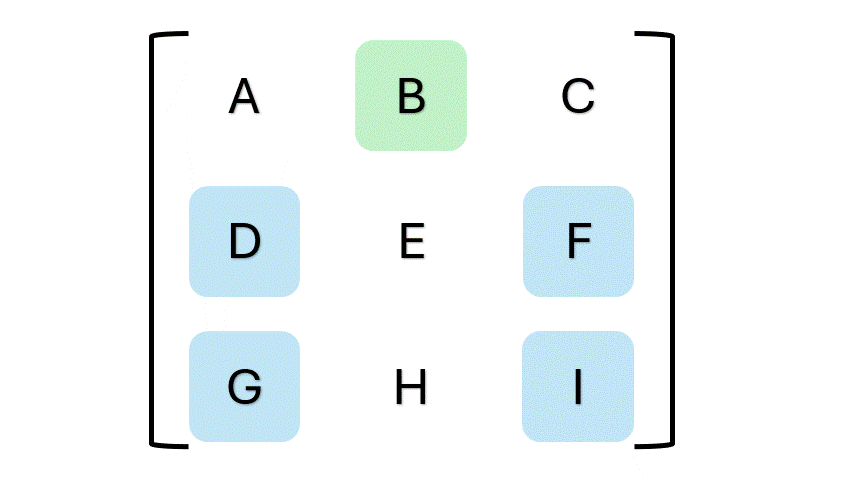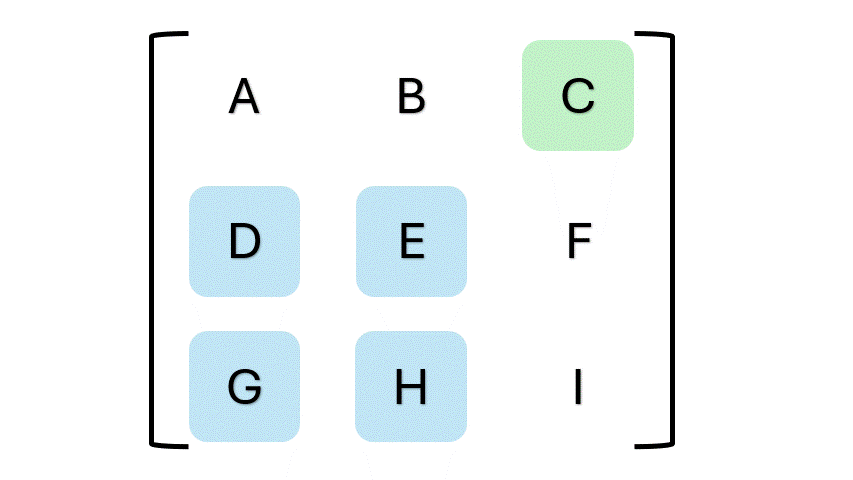
动图由作者提供
大多数线性回归问题会有超过三个观测值,也就是有很多行。对于更大的矩阵,你可以用的一个方法是拉普拉斯展开,公式如下:
det ( A ) = ∑ j = 1 n ( − 1 ) 1 + j a 1 j × det ( M 1 j ) \text{det}(\mathbf{A}) = \sum_{j=1}^{n} (-1)^{1+j} a_{1j} \times \text{det}(\mathbf{M}_{1j}) det(A)=j=1∑n(−1)1+ja1j×det(M1j)
公式的第一部分代表前面说的正负号规律。变量 a 1 j a_{1j} a1j 是矩阵第一行第 j j j 列的元素,最后的 M 1 j \mathbf{M}_{1j} M1j 是对应变量 a 1 j a_{1j} a1j 的余子式矩阵。要是 M 1 j \mathbf{M}_{1j} M1j也是一个大矩阵呢?那你还得再做一次拉普拉斯展开。如你所见,这个过程很快就会变得计算量很大。
接下来是矩阵 A 的伴随矩阵。矩阵的伴随矩阵就是余子式矩阵的转置。所以,咱们先用下面这个公式计算矩阵 A 中每个变量的余子式。注意, C C C 表示余子式。我还给出了第一行变量的详细计算过程,是不是有点眼熟?
C i j = ( − 1 ) i + j × det ( M i j ) C_{ij} = (-1)^{i+j} \times \text{det}(\mathbf{M}_{ij}) Cij=(−1)i+j×det(Mij)
C 11 = det [ e f h i ] , C 12 = − det [ d f g i ] , C 13 = det [ d e g h ] C_{11} = \text{det} \begin{bmatrix} e & f \\ h & i \end{bmatrix}, \quad C_{12} = -\text{det} \begin{bmatrix} d & f \\ g & i \end{bmatrix}, \quad C_{13} = \text{det} \begin{bmatrix} d & e \\ g & h \end{bmatrix} C11=det[ehfi],C12=−det[dgfi],C13=det[dgeh]
之后,你再取转置,到这里为止,咱们已经讲完了求解向量 B \mathbf{B} B 所需的所有内容!
def fit(self):"""使用训练数据拟合模型。"""# 在 X_train 中添加一列 1,用于截距项X_train_intercept = np.hstack([np.ones((self.X_train.shape[0], 1)), self.X_train])# 使用正规方程求解系数self.coefficients = np.linalg.inv(X_train_intercept.T @ X_train_intercept) @ X_train_intercept.T @ self.y_train
预测方法和预测新数据方法
咱们的模型对象已经具备了预测所需的一切,所以接下来咱们添加一个 predict 方法。这个方法会接收任意一组特征数组,利用咱们的 coefficients 属性来计算预测值。注意,咱们在特征矩阵 X \mathbf{X} X 的第一列额外添加了一列 1。还记得为啥要这么做吗?因为 coefficients 属性中的第一组权重是咱们的 X X X 截距,也就是 B 0 B_0 B0。
咱们还加了一个叫 predict_new 的方法,可以用它来预测一组新的特征值。
def predict(self, X):"""预测给定特征矩阵 X 的目标值。"""# 在 X 中添加一列 1,用于截距项X_intercept = np.hstack([np.ones((X.shape[0], 1)), X])return X_intercept @ self.coefficientsdef predict_new(self, new_features):"""预测一组新特征值的目标值。"""# 确保 new_features 是一个二维数组new_features = np.array(new_features).reshape(1, -1)return self.predict(new_features)[0]
评估方法
最后一步,咱们需要评估咱们的模型。这个方法会在咱们的 train_test_split 方法创建的测试数据上进行预测。有了预测值之后,咱们就可以评估咱们模型的性能了。为了实现这个目标,咱们会计算三种我个人非常喜欢的回归模型评估指标:均方误差、平均绝对误差和决定系数 R 2 R^2 R2。咱们不依赖外部模块来计算这些指标,而是自己动手写代码实现!
均方误差就是预测值与实际值之差的平方的平均值。平均绝对误差就是预测值与实际值之差的绝对值的平均值。 R 2 R^2 R2 可以说是非常独特的,因为它告诉咱们目标变量的变异性有多少是被模型解释的。你也可以把它定义为模型相比每次都直接预测目标变量的平均值要精确多少。我发现对于这两种定义有一些争论,所以咱们还是详细讲讲它到底是怎么计算的吧。这个指标是用 1 减去残差平方和与总平方和的比值来计算的。残差平方和是预测值与实际值之差的平方和。总平方和和它很像,只不过差值是实际值与平均值之间的。现在,如果分子和分母相比平均值来说差距很小的话,你可以推测模型在最小化误差方面做得很好,因为你是在用 1 减去这个值,所以 R 2 R^2 R2 值越接近 1,就说明模型越好。当它接近 0 的时候,你还不如直接用平均值来预测目标变量呢,所以模型可能不太好。也有可能出现负的 R 2 R^2 R2 值,这就意味着你的模型拟合得非常差。
def evaluate(self):"""使用 \(R^2\)、均方误差(MSE)和平均绝对误差(MAE)在测试数据上评估模型。"""y_pred = self.predict(self.X_test)mse = np.mean((self.y_test - y_pred) ** 2)mae = np.mean(np.abs(self.y_test - y_pred))r2 = 1 - np.sum((self.y_test - y_pred) ** 2) / np.sum((self.y_test - np.mean(self.y_test)) ** 2)return {"\(R^2\)": r2, "MSE": mse, "MAE": mae}
把所有内容整合起来
咱们来测试一下咱们的模型类!首先,咱们导入一些数据。咱们会用到 Kaggle 上的 加州房价数据集(CC0)。
df = pd.read_csv('housing.csv')
df.head()

咱们来聊聊这个数据集。housing 数据集大概有 20,000 行,包含了和房屋属性相关的各种特征。咱们会用这个数据来搭建一个多元线性回归模型,用这个数据集中的一些数值特征来预测中位房价。
首先,咱们把数据分成特征和目标变量。
X = df[['housing_median_age','total_rooms','total_bedrooms','median_income']]
y = df['median_house_value']
接下来,咱们用咱们的多元线性回归类,把数据分成训练集和测试集,训练模型,然后评估它。因为咱们的类已经做了大部分的重活儿,所以咱们只需要四行代码就能搞定!
MLR = MultipleLinearRegression()
MLR.train_test_split(X = X,y=y,train_size = 0.8, random_state=42)
MLR.fit()
MLR.evaluate()

咱们的模型在预测房价方面似乎做得还不错,看看 sklearn 的表现会不会更好。
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error,mean_absolute_error, r2_scoreX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
sklearn_lingreg = LinearRegression()
sklearn_lingreg.fit(X_train, y_train)y_pred = sklearn_lingreg.predict(X_test)mse = mean_squared_error(y_test, y_pred)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)print("\(R^2\):", r2)
print("均方误差(MSE):", mse)
print("平均绝对误差(MAE):", mae)

结果几乎一模一样!希望大家都从这个练习中学到了一些有价值的东西。如今,从 0 到 model.fit() 的过程似乎变得太容易了,这可能会让人忽视了驱动 AI 和机器学习不断发展的模型背后的数学原理。我强烈建议每一位读者自己动手做这个练习,说不定在这个过程中,你还能创造出更适合你用例的模型呢。
哇塞,这一路走过来,咱们不仅从零搭建了一个线性回归模型,还成功地把它跑起来了!从数据预处理、归一化,到实现数学公式,再到用梯度下降找到最优权重,每一步都充满了挑战,但咱们都一一搞定了。最重要的是,咱们还和 sklearn 的大神级模型比了一把,结果发现,咱们的模型一点都不逊色!这感觉,就像自己做的手工汉堡,虽然简单,但吃起来格外香!🎉
