软考-软件设计师中级备考 6、数据结构 图

1. 有向图

有向图是由顶点集合 V 和有向边集合 E 组成的图结构。在有向图中，边是有方向的，即从一个顶点指向另一个顶点，通常用有序对 (u, v) 表示，其中 u 是边的起始顶点，v 是边的终止顶点。例如，在一个表示任务依赖关系的图中，有向边可以表示任务 u 完成后才能开始任务 v。

2. 无向图

无向图同样由顶点集合 V 和边集合 E 组成，但边是没有方向的。边用无序对 (u, v) 表示，意味着顶点 u 和顶点 v 之间存在连接，且从 u 到 v 和从 v 到 u 是等价的。比如在一个城市交通图中，连接两个城市的道路可以看作无向边，因为车辆可以在这条道路上双向行驶。

3. 完全图

• 对于无向完全图，在一个具有 n 个顶点的无向图中，如果任意两个顶点之间都存在一条边，那么这个图就是无向完全图。其边的数量为 。
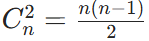• 对于有向完全图，在一个具有 n 个顶点的有向图中，如果任意两个顶点u和v之间都存在两条有向边，一条从u指向v，另一条从v指向u，则该图为有向完全图。其边的数量为 n(n - 1) 。

4. 度

• 在无向图中，顶点的度是指关联于该顶点的边的数量。例如，一个顶点连接了 3 条边，那么它的度就是 3。
• 在有向图中，顶点的度分为入度和出度。入度是指以该顶点为终点的有向边的数量；出度是指以该顶点为起点的有向边的数量。顶点的度等于其入度与出度之和。

5. 邻接矩阵（存储结构）

邻接矩阵是一种用于表示图的存储结构。对于一个具有 n 个顶点的图，我们可以用一个 n×n 的矩阵来表示。

• 对于无向图，如果顶点 i 和顶点 j 之间有边相连，则邻接矩阵 A[i][j] = A[j][i] = 1；否则 A[i][j] = A[j][i] = 0。
• 对于有向图，如果存在从顶点 i 到顶点 j 的有向边，则邻接矩阵 A[i][j] = 1，否则 A[i][j] = 0。如果图是带权图，矩阵中存储的就是边的权值，无边相连的顶点之间用一个特殊的较大值（如无穷大）表示。

6. 拓扑排序

拓扑排序是对有向无环图（DAG）的顶点进行排序的一种方法，使得对于图中的任意一条有向边 (u, v)，在排序结果中 u 都排在 v 之前。拓扑排序常用于解决任务调度等问题，例如在一个项目中，有多个任务之间存在依赖关系，拓扑排序可以确定任务的执行顺序。常见的拓扑排序算法有 Kahn 算法和深度优先搜索（DFS）的变形。

7. 最小生成树（克鲁斯卡尔算法）

最小生成树是在一个连通的无向带权图中，由图中部分边构成的一个子图，该子图包含图中的所有顶点，且是一个连通的树结构，并且其边的权值之和最小。 克鲁斯卡尔算法是用于求解最小生成树的一种贪心算法，步骤如下：

1. 将图中所有的边按照权值从小到大进行排序。
2. 初始化一个空的最小生成树集合 T。
3. 依次检查排序后的每条边，如果将这条边加入 T 后不会形成环，则将其加入 T 中。
4. 重复步骤 3，直到 T 中包含了 n - 1条边（n 为图中顶点的数量），此时 T 就是该图的最小生成树。