低功耗蓝牙BLE之高斯频移键控（GFSK）

概要

在数字通信中，频率偏移键控（Frequency Shift Keying, FSK）是一种调制技术，用于将数字信号转换成模拟信号以便在信道中传输。而在实际应用中，为了进一步提高频谱效率或适应特定的通信协议，可以使用广义频率偏移键控（Generalized FSK, GFSK），它通过调整每个符号的频率偏移量来优化性能。

波形特性:
a. 带宽效率：GFSK相比于BPSK和PSK有更宽的带宽效率，因为它允许更快的频率变化。
b. 抗干扰能力：由于频率的变化不是连续的，GFSK比BPSK有更好的抗干扰性能。
c. 实现：在实际中，GFSK可以通过数字信号处理器（DSP）来实现，通过调整采样点附近的数字信号的频率来实现精确的调制。

实际应用中的考虑:
在实现GFSK时，重要的是确保 $\Delta f$ 的选择既足够小以保持信号的相似性，又足够大以避免混叠问题并保持足够的带宽效率。
此外，滤波器的设计也是关键，以确保在接收端正确地恢复出原始的基带信号。

GFSK调制分析

GFSK 调制的基本原理
GFSK 通过调整每个符号的频率偏移量来实现，使得在每个符号的持续时间内的频率变化更加平滑。这通常是通过使用一个高斯（或近似高斯）滤波器来实现的，使得频率的变化在时间上是连续的，而不是像传统的FSK那样在符号边界处突变。

GFSK 传输0和1的示例
假设我们使用一个基本的GFSK调制方案，其中0和1分别对应于不同的频率偏移。

例如：
0 对应于基础频率 $ f_0 $

1 对应于 $ f_0 + \Delta f $

其中 $ \Delta f $ 是频率偏移量。

调制过程：
0 的调制：当发送0时，整个符号周期内的频率保持为 $ f_0 $。

1 的调制：当发送1时，信号的频率在整个符号周期内线性增加从 $ f_0 $ 到 $ f_0 + \Delta f $。

数学表示：
对于单个符号周期 $ T $ 和采样频率 $ F_s $，我们可以这样表示：

对于0：$ s(t) = A \cos(2 \pi f_0 t) $

对于1：$ s(t) = A \cos(2 \pi (f_0 + \frac{\Delta f}{2}) t + \pi
\frac{\Delta f}{2} t^2) $

这里，$ A $ 是振幅，$ t $ 是时间，$ \pi \frac{\Delta f}{2} t^2 $ 确保了频率随时间平滑变化。

Python仿真代码

使用Python和NumPy库，我们可以生成GFSK调制信号的示例：

import numpy as np
import matplotlib.pyplot as plt# 参数设置
fs = 100000  # 采样频率
f0 = 10000  # 基础频率
delta_f = 5000  # 频率偏移量
T = 1/f0  # 符号周期
N = int(T * fs)  # 一个符号周期内的样本数
t = np.arange(N*10) / fs  # 时间向量# 生成GFSK信号
A = 1  # 振幅
signal_0 = A * np.cos(2 * np.pi * f0 * t)  # 0的调制信号
signal_1 = A * np.cos(2 * np.pi * (f0 + delta_f/2) * t + np.pi * delta_f/2 * t**2)  # 1的调制信号# 绘制信号
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(t, signal_0)
plt.title('GFSK Modulation Symbol- 0')
plt.subplot(2, 1, 2)
plt.plot(t, signal_1)
plt.title('GFSK Modulation Symbol- 1')
plt.tight_layout()
plt.show()

这段代码将生成并显示两个GFSK调制信号，一个表示发送0，另一个表示发送1。通过这种方式，我们可以观察到频率如何在符号周期内平滑变化。

仿真时域分析

如下图所示，

那么，0/1 对应的频率分别是10000Hz , 12500Hz。

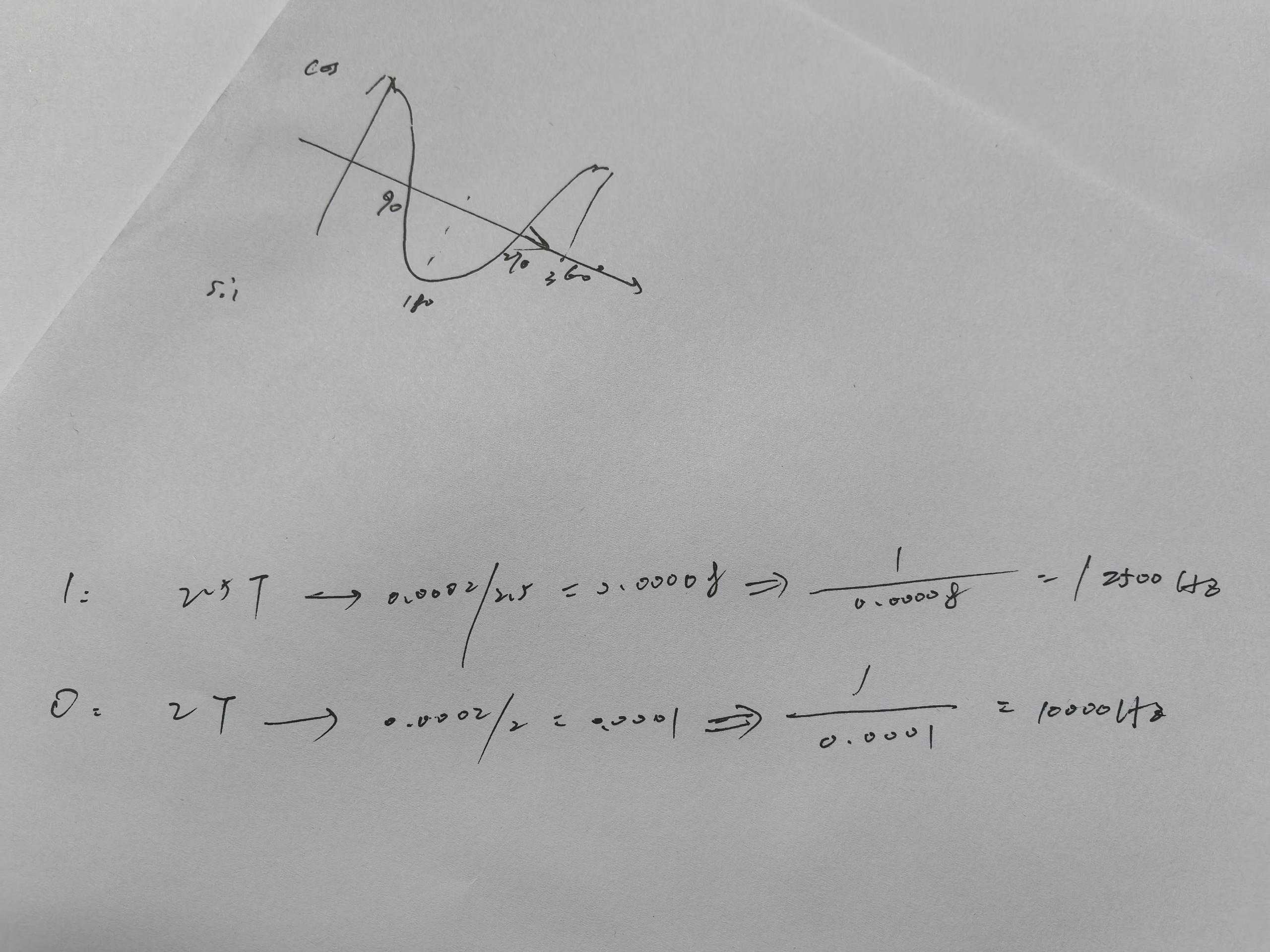
技术点一：python数据操作numpy

在Python中，使用NumPy库进行数据操作是一种非常高效和强大的方式。
NumPy是一个开源的Python库，用于进行科学计算，特别是在数组计算方面。

下面介绍一些基本的应用：
创建数组
NumPy的核心是ndarray对象，一个存储单一数据类型的多维数组。你可以使用多种方式创建数组：

从Python列表创建数组，
arr = np.array([1, 2, 3, 4, 5])

创建特定形状和类型的数组，默认类型为float，
arr_zeros = np.zeros((3, 4)) # 3x4的零矩阵
arr_ones = np.ones((2, 3)) # 2x3的矩阵，元素全为1
arr_range = np.arange(10) # 等价于range(10)，但返回的是数组

数组的基本操作
访问元素和切片
print(arr[0]) # 访问第一个元素
print(arr[1:4]) # 访问第二个到第四个元素（不包括第四个）
print(arr_zeros[1, 2]) # 访问2x4矩阵的第二行第三列的元素
修改数组元素
arr[0] = 10 # 将第一个元素改为10
arr_zeros[0, 0] = 5 # 将2x4矩阵的第一行第一列的元素改为5
数组运算
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
print(a + b) # 元素加法，输出 [5, 7, 9]
print(a * b) # 元素乘法，输出 [4, 10, 18]
print(a @ b) # 矩阵乘法，输出单个数字或数组，取决于a和b的形状

数组的广播机制
NumPy的广播机制允许不同形状的数组进行算术运算：

a = np.array([[1, 2], [3, 4]])
b = np.array([10, 20])
print(a + b) # b会被广播以匹配a的形状，输出 [[11, 22], [13, 24]]

使用函数进行数组操作
NumPy提供了大量的数学函数，可以直接应用于数组：

a = np.array([1, 2, 3, 4])
print(np.sqrt(a)) # 对每个元素求平方根，输出 [1. 1.41421356 1.73205081 2. ]
print(np.sin(a)) # 对每个元素应用sin函数，输出 [-0.84147098 0.90929743 0.14112001 1.29846218]

索引和切片更高级的使用
a = np.arange(12).reshape(3, 4) # 重塑为3x4矩阵
print(a) # 查看数组结构
print(a[1:, 1:]) # 从第二行第二列开始的所有元素（不包括第二行第二列）
print(a[a > 5]) # 所有大于5的元素组成的新数组 [ 6 7 8 9 10 11]

技术点二：SIN /COS函数图像性质

COS周期

参考文章

FSK调制原理

ASK,OOK,FSK,GFSK简介

Datawhale 数学建模

小结

• 在无线通信系统中，GFSK（Gaussian Frequency Shift Keying）是一种调制技术，用于将数字信号（0和1）转换为模拟信号以便于无线传输。

• GFSK通过改变载波频率的形状来实现数据传输，这使得它在抗噪声和频谱效率方面优于简单的FSK（Frequency Shift Keying）技术。

愿你我心中有光，脚下有力，共赴人生的精彩旅程，共勉。