C++蓝桥杯实训篇(四)
片头
嗨!小伙伴们,大家好~ 今天我们来介绍二分法,准备好了吗?咱们开始咯!

咱们先画个图~

因此,整数二分步骤如下:
①找一个区间[L,R],使得答案一定在该区间中
②找一个判断条件,使得判断条件具有二段性,并且答案一定是二段性的分界点
③分析中点mid在该判断条件下是否成立,如果成立,考虑答案在哪个区间;如果不成立,考虑答案在哪个区间
④如果更新方式写的是 R == mid,则不做任何处理;
如果更新方式写的是 L == mid,则需要在计算mid时+1
下面我们来看一道例题:
第1题 数的范围

emmm,这道题需要我们求出元素的起始位置和终止位置,就运用到了我们上面讲的二分法

先找出第1次x出现的位置,也就是大于等于x的第1个位置
const int N = 10086;
int n, m;
int a[N];
int main() {
cin >> n >> m; //n代表数组里面共有n个元素
//m代表询问个数
for (int i = 0; i < n; i++) {
scanf("%d", &a[i]);
}
for (int i = 0; i < m; i++) {
int x;
scanf("%d", &x);
//找左端点: ≥x的第1个位置
int L = 0, R = n - 1;
while (L < R) {
int mid = (L + R) / 2;
if (a[mid] >= x) R = mid;
else L = mid + 1;
}
if (a[R] == x) cout << R << endl; //如果找到了,将该点的坐标输出
else printf("-1 -1\n"); //如果没找到,输出-1 -1即可
}
return 0;
}运行结果如下:

找到左端点了,咱们再去找找右端点吧~

const int N = 10086;
int n, m;
int a[N];
int main() {
cin >> n >> m; //n代表数组里面共有n个元素
//m代表询问个数
for (int i = 0; i < n; i++) {
scanf("%d", &a[i]);
}
for (int i = 0; i < m; i++) {
int x;
scanf("%d", &x);
//找左端点: ≥x的第1个位置
int L = 0, R = n - 1;
while (L < R) {
int mid = (L + R) / 2;
if (a[mid] >= x) R = mid;
else L = mid + 1;
}
if (a[R] == x) {
cout << R << " "; //将左端点输出
R = n - 1; //更新R的位置
//找右端点: [左端点,n-1]
while (L < R) {
int mid = (L + R + 1) / 2;
if (a[mid] <= x) L = mid;
else R = mid - 1;
}
cout << R << endl; //输出右端点
}
else printf("-1 -1\n"); //如果没找到,输出-1 -1即可
}
return 0;
}运行结果如下:

还是这道题,但是我们采用另一种方法~

咱们可以先画个图,就容易理解啦~

我们先寻找"3"的左端点
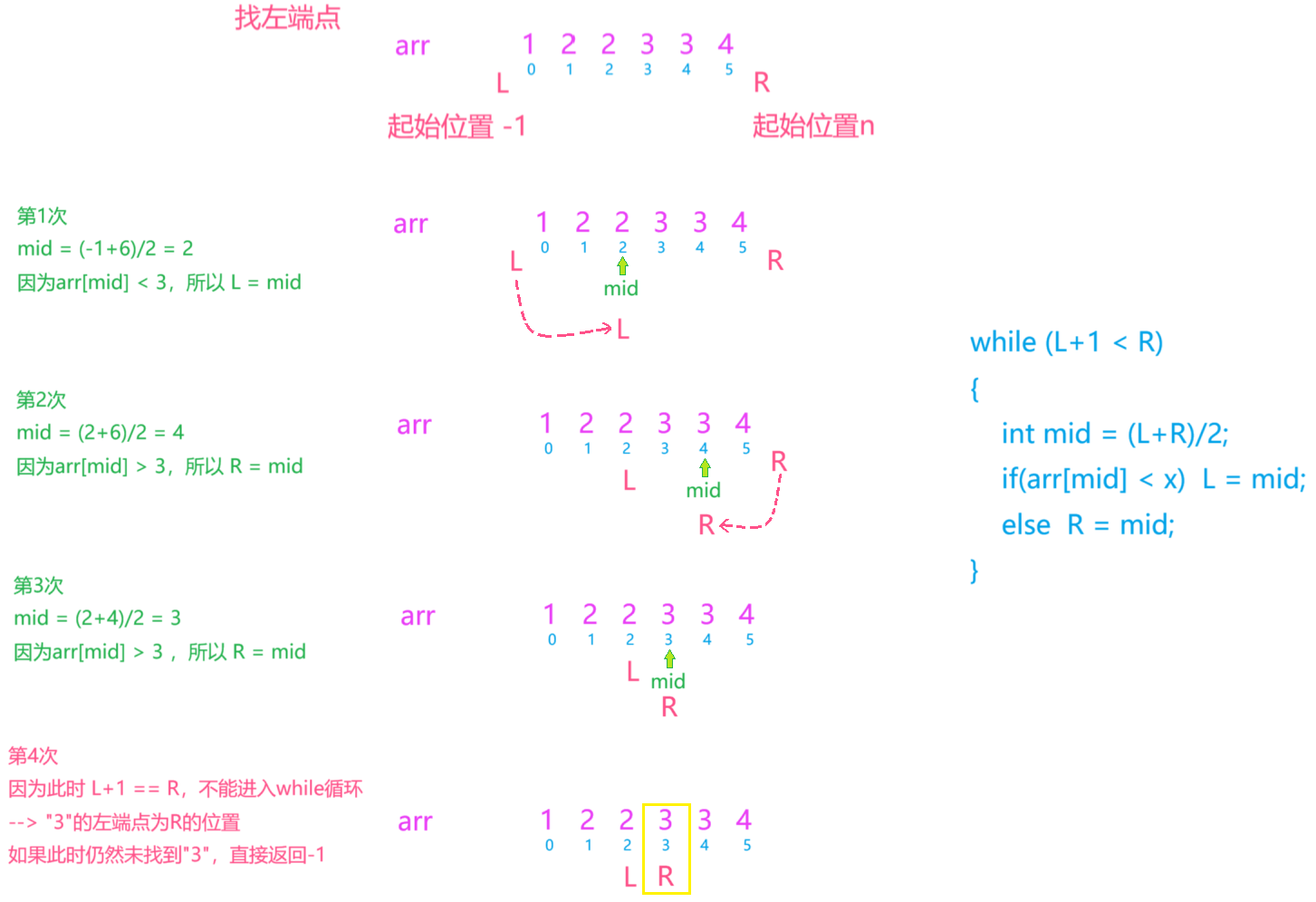
我们再来寻找"3"的右端点

OK啦,以上是"3"的左右端点画图分析过程,接下来咱们用代码来实现~
方法和原来的步骤基本类似,我们依然先在main函数外面定义全局变量。
const int N = 1e5 + 100; //N代表数组的大小,必须比题目给的范围大才行
int arr[N]; //原始数组
int n; //数组长度
int q; //询问个数接着在main函数中输入n个元素,并进行q次询问(while循环)。定义变量r1和r2分别代表左右端点。如果r1和r2找到了,直接输出即可;如果没有找到,那么输出 "-1 -1" 。
//输入n个元素
cin >> n >> q;
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
//q次询问
while (q--) {
int x;
cin >> x;
int r1 = binary_search1(arr, x); //左端点
int r2 = binary_search2(arr, x); //右端点
cout << r1 << " " << r2 << endl; //将r1和r2输出
}OK,整体框架搭好后,咱们可以实现二分查找函数了~
先来实现查找左端点
//数组中的数是num,被询问的数是x
bool isBlue1(int num, int x) {
if (num < x) return true;
else return false;
}
//第1个二分查找找的是: 被询问数的第1次出现的位置(下标)
int binary_search1(int arr[], int x) {
int L = -1, R = n;
while (L + 1 < R) {
int mid = (L + R) / 2;
if (isBlue1(arr[mid], x)) L = mid;
else R = mid;
}
if (arr[R] == x) return R;
else return -1; //找不到就返回-1
}再来实现查找右端点
//数组中的数是num,被询问的数是x
bool isBlue2(int num, int x) {
if (num <= x) return true;
else return false;
}
//第2个二分查找找的是: 被询问数的最后1次出现的位置(下标)
int binary_search2(int arr[], int x) {
int L = -1, R = n;
while (L + 1 < R) {
int mid = (L + R) / 2;
if (isBlue2(arr[mid], x)) L = mid;
else R = mid;
}
if (arr[L] == x) return L;
else return -1; //找不到就返回-1
}OK啦,整道题的代码如下:
#include<iostream>
using namespace std;
//数的范围
const int N = 1e5 + 100; //N代表数组的大小,必须比题目给的范围大才行
int arr[N]; //原始数组
int n; //数组长度
int q; //询问个数
//数组中的数是num,被询问的数是x
bool isBlue1(int num, int x) {
if (num < x) return true;
else return false;
}
//第1个二分查找找的是: 被询问数的第1次出现的位置(下标)
int binary_search1(int arr[], int x) {
int L = -1, R = n;
while (L + 1 < R) {
int mid = (L + R) / 2;
if (isBlue1(arr[mid], x)) L = mid;
else R = mid;
}
if (arr[R] == x) return R;
else return -1; //找不到就返回-1
}
//数组中的数是num,被询问的数是x
bool isBlue2(int num, int x) {
if (num <= x) return true;
else return false;
}
//第2个二分查找找的是: 被询问数的最后1次出现的位置(下标)
int binary_search2(int arr[], int x) {
int L = -1, R = n;
while (L + 1 < R) {
int mid = (L + R) / 2;
if (isBlue2(arr[mid], x)) L = mid;
else R = mid;
}
if (arr[L] == x) return L;
else return -1; //找不到就返回-1
}
int main() {
//输入n个元素
cin >> n >> q;
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
//q次询问
while (q--) {
int x;
cin >> x;
int r1 = binary_search1(arr, x); //左端点
int r2 = binary_search2(arr, x); //右端点
cout << r1 << " " << r2 << endl; //将r1和r2输出
}
return 0;
}我们可以对代码进行优化:
//第1个二分查找找的是: 被询问数的第1次出现的位置(下标)
int binary_search1(int arr[], int x) {
int L = -1, R = n;
while (L + 1 < R) {
int mid = (L + R) / 2;
if (arr[mid] < x) L = mid;
else R = mid;
}
if (arr[R] == x) return R;
else return -1; //找不到就返回-1
}
//第2个二分查找找的是: 被询问数的最后1次出现的位置(下标)
int binary_search2(int arr[], int x) {
int L = -1, R = n;
while (L + 1 < R) {
int mid = (L + R) / 2;
if (arr[mid] <= x) L = mid;
else R = mid;
}
if (arr[L] == x) return L;
else return -1; //找不到就返回-1
}main函数部分也可以进行代码优化:
//q次询问
while (q--)
{
int x;
cin >> x;
int r1 = binary_search1(arr, x); //左端点
if (r1 == -1)
{
//如果左端点找不到,右端点一定找不到
//输出 -1 -1 即可
cout << "-1 -1" << endl;
continue; //跳过后续所有代码
}
int r2 = binary_search2(arr, x); //右端点
cout << r1 << " " << r2 << endl; //输出左右端点
}欧克欧克,优化后的整体代码如下:
#include<iostream>
using namespace std;
//数的范围
const int N = 1e5 + 100; //N代表数组的大小,必须比题目给的范围大才行
int arr[N]; //原始数组
int n; //数组长度
int q; //询问个数
//第1个二分查找找的是: 被询问数的第1次出现的位置(下标)
int binary_search1(int arr[], int x) {
int L = -1, R = n;
while (L + 1 < R) {
int mid = (L + R) / 2;
if (arr[mid] < x) L = mid;
else R = mid;
}
if (arr[R] == x) return R;
else return -1; //找不到就返回-1
}
//第2个二分查找找的是: 被询问数的最后1次出现的位置(下标)
int binary_search2(int arr[], int x) {
int L = -1, R = n;
while (L + 1 < R) {
int mid = (L + R) / 2;
if (arr[mid] <= x) L = mid;
else R = mid;
}
if (arr[L] == x) return L;
else return -1; //找不到就返回-1
}
int main() {
//输入n个元素
cin >> n >> q;
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
//q次询问
while (q--)
{
int x;
cin >> x;
int r1 = binary_search1(arr, x); //左端点
if (r1 == -1)
{
//如果左端点找不到,右端点一定找不到
//输出 -1 -1 即可
cout << "-1 -1" << endl;
continue; //跳过后续所有代码
}
int r2 = binary_search2(arr, x); //右端点
cout << r1 << " " << r2 << endl; //输出左右端点
}
return 0;
}第2题 查找

这道题,是让我们输出数字在序列中第1次出现的编号,如果没找到,输出-1。其实是让我们输出左端点。
代码如下:
#include<iostream>
using namespace std;
//查找这个数第1次出现的位置
const int N = 1e6 + 100;
int n, m;
int arr[N];
int b_search(int arr[], int x) {
int L = 0, R = n + 1;
while (L + 1 < R) {
int mid = (L + R) / 2;
if (arr[mid] < x) L = mid;
else R = mid;
}
if (arr[R] == x) return R; //找到左端点
else return -1; //没有找到,返回-1
}
int main() {
//n表示数字个数,m表示询问次数
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> arr[i];
}
while (m--) {
int x;
cin >> x;
int r1 = b_search(arr, x); //求左端点
cout << r1 << " ";
}
cout << endl;
return 0;
}第3题 A-B数对

这道题,需要我们输出满足A-B=C的数对的个数。
我们可以定义2个类似于指针的变量,初始时,A指针指向第1个元素,B指针从第1个元素开始往后遍历,直到遍历完最后一个元素。A指针指向下一个元素,B指针重新从第1个元素开始往后遍历。以此类推,直到A指向最后1个元素。
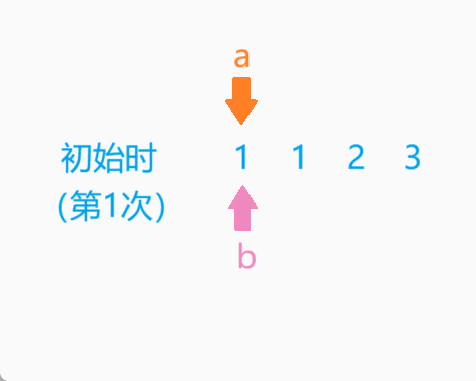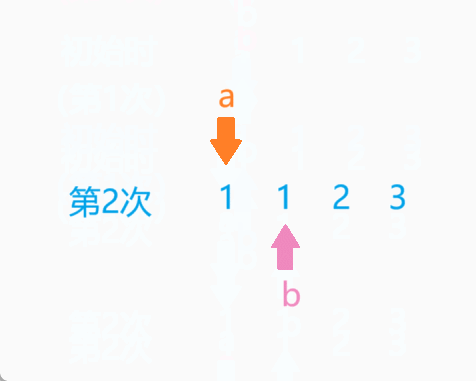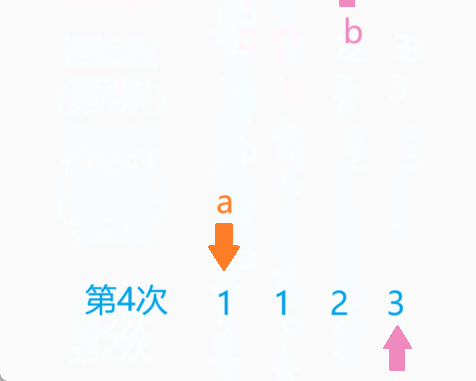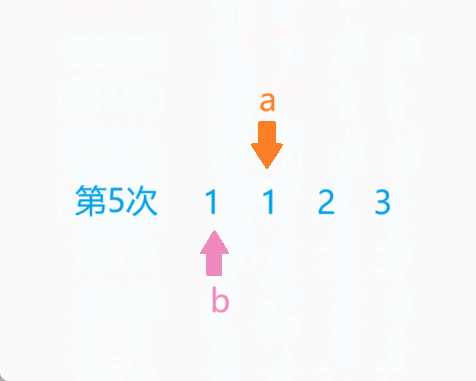
OK,实质上就是暴力枚举,具体代码如下:
//A-B数对
const int N = 2e5 + 100;
int n, c;
int arr[N];
//朴素法(暴力枚举)
int main() {
//n个正整数
//计算满足 A-B = C的数对的个数
cin >> n >> c;
for (int i = 1; i <= n; i++) {
cin >> arr[i];
}
int ans = 0; //计数
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (arr[i] - arr[j] == c) ans++;
}
}
cout << ans << endl;
return 0;
}但是光靠暴力,我们无法通过全部的测试,毕竟时间复杂度太大了。因此我们可以换一种思路~
想想看,题目要输出满足 A-B = C 的数对的个数,那么我们可以求满足 A = B+C 的数对个数,C是固定不变的,B从第1个元素开始,一直到最后1个元素结束。每一个B+C都对应1个A,我们需要在序列中找到A,统计次数count即可。
怎么找到A呢?
可以利用二分查找,如果一个序列中不同位置的数字一样(A相同),那么也算不同的数对,count+1。找到A第1次出现的位置,记作ret1;最后1次出现的位置,记作ret2。统计次数 count = ret2 - ret1 + 1。
可能小伙伴有疑问:如果当前这个B只出现1个与之相对应的A,count 怎么计算呢?
这也就相当于第1次出现A的位置和最后1次出现A的位置相同,ret1 == ret2 ,那么count = ret2 - re1 + 1 = 1。也就相同于 count++。(count只加了1次)
代码如下:
#include<iostream>
using namespace std;
const int N = 2e5 + 100;
int n, c;
int arr[N];
//找左端点
int Bin_search1(int arr[], int x) {
int L = 0, R = n + 1;
while (L + 1 < R) {
int mid = (L + R) / 2;
if (arr[mid] < x) L = mid;
else R = mid;
}
if (arr[R] == x) return R;
else return -1;
}
//找右端点
int Bin_search2(int arr[], int x) {
int L = 0, R = n + 1;
while (L + 1 < R) {
int mid = (L + R) / 2;
if (arr[mid] <= x) L = mid;
else R = mid;
}
if (arr[L] == x) return L;
else return -1;
}
//二分查找
int main() {
cin >> n >> c;
for (int i = 1; i <= n; i++) {
cin >> arr[i];
}
//先排序,再使用二分法
sort(arr + 1, arr + n + 1);
long long res = 0;
for (int B = 1; B <= n; B++) {
int A = arr[B] + c;
int r1 = Bin_search1(arr, A);
if (r1 == -1) {
continue;
}
int r2 = Bin_search2(arr, A);
res += r2 - r1 + 1; //求次数
}
cout << res << endl;
return 0;
}
注意:进行二分查找时,必须先进行排序!
第4题 砍树

emmm,咱们先画个图理解一下~

我们可以先采用朴素算法(暴力枚举),锯片的高度从最高的树的高度开始,慢慢往下移动,直到满足需要的木材总长度。
#include<iostream>
using namespace std;
//砍树问题
const int N = 1e6 + 100;
int n, m;
int arr[N];
int main() {
//n表示树木的数量
//m表示需要的木材总高度
cin >> n >> m;
int highest = 0;
for (int i = 1; i <= n; i++) {
cin >> arr[i];
highest = max(highest, arr[i]); //找到树木的最高值
}
int sum = 0; //记录当前得到的树的总高度
int ret = 0; //锯片的高度
for (int i = hightest; i >= 1; i--) {
sum = 0;//每次sum都要清零
for (int j = 1; j <= n; j++) {
sum += max(0, arr[j] - i);
if (sum >= m) break; //提前终止
}
if (sum >= m) {
ret = i;
break; // 找到最大高度直接退出
}
}
cout << ret << endl;
return 0;
}当然啦,朴素算法的时间复杂度很大,因此我们可以用二分查找来解决~
#include<iostream>
using namespace std;
const int N = 1e6 + 100;
int n, m;
int arr[N];
typedef long long ll;
//x: 枚举的当前锯片的高度
bool check(ll x) {
ll sum = 0;
for (int i = 1; i <= n; i++) {
sum += max(0ll,arr[i] - x);
}
if (sum >= m) return true;
else return false;
}
int main() {
//n表示树木的数量
//m表示需要的木材总高度
cin >> n >> m;
int highest = 0; //树木的最高高度
for (int i = 1; i <= n; i++) {
cin >> arr[i];
highest = max(highest, arr[i]);
}
//二分查找
//L: 最小高度 0
//R: 最大高度 highest+1
ll L = 0, R = highest + 1;
while (L + 1 < R) {
ll mid = (L + R) / 2;
if (check(mid)) L = mid;
else R = mid;
}
if (check(R)) printf("%lld\n", R);
else printf("%lld\n", L);
return 0;
}片尾
今天我们学习了二分查找相关知识,希望看完这篇文章能对友友们有所帮助!!!
求点赞收藏加关注!!!
谢谢大家!!!

