Python学习笔记(列表相关操作)
列表相关操作
- 第17节课 列表相关操作
- 1 常规操作
- 2 查找操作
- 3 排序操作
第17节课 列表相关操作
无论是内置函数、对象函数,用起来确实很方便,但是作为初学者,你必须懂得它们背后的运行逻辑!
1 常规操作
(1)遍历
arr = [1,2,3,4]
# 以索引遍历:可以在遍历期间修改元素
for index in range(len(arr)):
arr[index] = arr[index] ** 2
print(arr[index])
print(arr)
# 以元素遍历:只能获取元素,不能修改元素值(可变对象除外)
for element in arr:
print(element)
# 同时遍历角标和元素
for index, element in enumerate(arr):
print(f"角标{index},元素{element}")
# 反向遍历
for index in range(len(arr) - 1, -1, -1):
print(arr[index])
(2)最值
def min_max(arr:list[int]) -> tuple:
min_value = arr[0]
max_value = arr[0]
for i in range(1, len(arr)):
if arr[i] > max_value:
max_value = arr[i]
if arr[i] < min_value:
min_value = arr[i]
return min_value, max_value
arr = [2,9,8,1,7,4,6,3,5]
min_val, max_val = min_max(arr)
print(min_val, max_val)
(3)存在性
arr = [2,9,8,1,7,4,6,3,5]
#O(n)
def is_exist(arr:list[int], key:int) -> bool:
for element in arr:
if element == key:
return True
return False
print(is_exist(arr, 10))
print(is_exist(arr, 8))
(4)反转
arr = [1,2,3,4,5,6,7,8,9]
"""
1 2 3 4 5 6 7 8 9
l
r
"""
def list_reverse(arr:list[int]) -> None:
l = 0
r = len(arr) - 1
while l < r:
arr[l], arr[r] = arr[r], arr[l]
l += 1
r -= 1
list_reverse(arr)
print(arr)
(5)乱序
import random
arr = [1,2,3,4,5,6,7,8,9]
def list_shuffle(arr):
for i in range(len(arr)):
j = random.randint(0, len(arr) - 1)
arr[i], arr[j] = arr[j], arr[i]
list_shuffle(arr)
print(arr)
(6)二维列表
所谓的二维列表,其实本质上就是一个一维列表,只不过该一维列表中的每一个元素为其他的一维列表
def print_matrix(matrix):
for i in range(len(matrix)):
for j in range(len(matrix[i])):
print(matrix[i][j], end = ' ')
print()
# 直接填值创建二维列表
matrix = [[1,2,3], [4,5,6], [7,8,9]]
print(len(matrix))
print(len(matrix[1]))
print_matrix(matrix)
matrix = [
[1,2,3,4],
[1,2,3],
[1,2],
[1]
]
print_matrix(matrix)
# 循环创建二维列表 指定默认值 0
rows = 3
cols = 5
matrix = []
for i in range(rows):
row = [0] * cols
matrix.append(row)
matrix[2][2] = 6
print_matrix(matrix)
# 列表推导式创建二维列表
matrix = [[0] * cols for _ in range(rows)]
matrix[2][2] = 6
print_matrix(matrix)
matrix = [ [i + j for j in range(cols)] for i in range(rows)]
print_matrix(matrix)
2 查找操作
(1)二分查找

前提数据必须是有序的(升序、降序)
# 返回的是元素key在arr中的角标 如果不存在则返回-1
def binary_search(arr, key): #O(log n)
left = 0
right = len(arr) - 1
mid = (left + right) // 2
while arr[mid] != key:
if arr[mid] < key:
left = mid + 1
elif key < arr[mid]:
right = mid - 1
if left > right:
return -1
# 重新更新mid的值
mid = (left + right) // 2
return mid
# 顺序查找
def linear_search(arr, key):
for index in range(len(arr)):
if arr[index] == key:
return index
return -1
# arr = [1,2,3,4,5,6,7,8,9]
# key = 6
# print(binary_search(arr, key))
"""
n/2/2/2/2/..../2 = 1
n/2^x = 1
n = 2^x
x = logn
"""
arr = []
for i in range(70000000):
arr.append(i)
key = 69999999
print("数据创建完毕...")
print(binary_search(arr, key))
print(linear_search(arr, key))
(2)插值查找
前提数据必须是有序的(升序、降序),它是二分查找的升级版本
# mid = (key - arr[left]) / (arr[right] - arr[left]) * (right - left) + left
# 当数据分布比较均匀的时候 大致满足等差序列的情况 性能要比二分查找要优秀
def interpalotion_search(arr, key):
count = 0
left = 0
right = len(arr) - 1
mid = 0
# mid = int((key - arr[left]) / (arr[right] - arr[left]) * (right - left)) + left
# while arr[mid] != key:
# count += 1
# if arr[mid] < key:
# left = mid + 1
# elif key < arr[mid]:
# right = mid - 1
# if left > right:
# mid = -1
# break
# mid = int((key - arr[left]) / (arr[right] - arr[left]) * (right - left)) + left
while True:
count += 1
mid = int((key - arr[left]) / (arr[right] - arr[left]) * (right - left)) + left
# key本身在范围外 没找到
if mid < left or mid > right:
mid = -1
break
if arr[mid] < key:
left = mid + 1
elif key < arr[mid]:
right = mid - 1
else:
break
# 在范围内没找到
if left > right:
mid = -1
break
print(f"插值查找count={count}")
return mid
def binary_search(arr, key): #O(log n)
count = 0
left = 0
right = len(arr) - 1
mid = (left + right) // 2
while arr[mid] != key:
count += 1
if arr[mid] < key:
left = mid + 1
elif key < arr[mid]:
right = mid - 1
if left > right:
mid = -1
break
# 重新更新mid的值
mid = (left + right) // 2
print(f"二分查找count={count}")
return mid
# int((20 - 1)/(20-1) * (19 - 0)) + 0 = 19
# int((100 - 1)/(20 - 1) * (19 - 0))+ 0 = 99
# int((-100 - 1)/(20 - 1)*(19-0)) + 0 = - 101
arr= [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]
key = -100
print(binary_search(arr, key))
print(interpalotion_search(arr, key))
3 排序操作
希尔排序、堆排序、快速排序、归并排序、计数排序、基数排序、桶排序
(1)选择排序
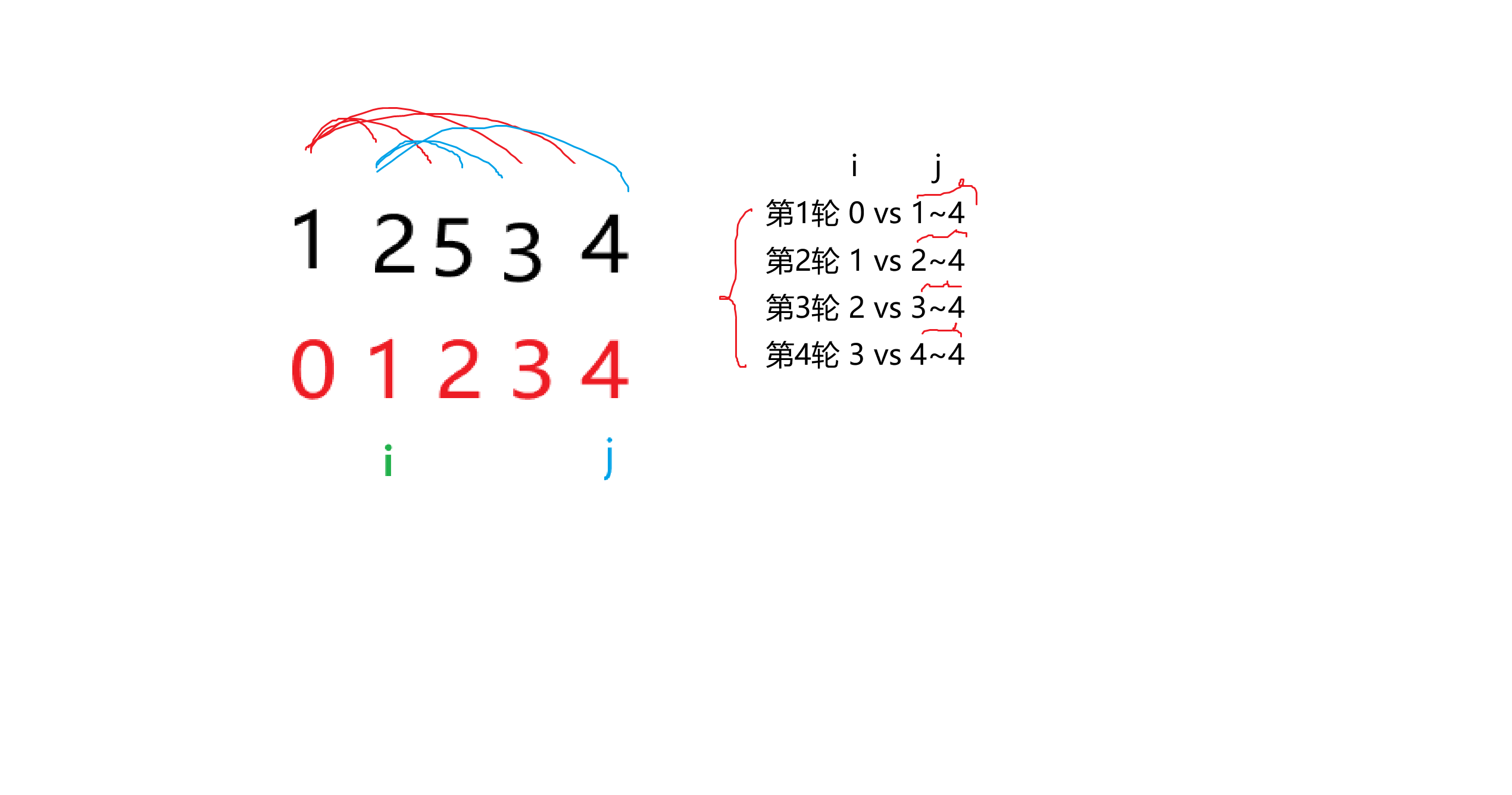
# 选择排序 O(n^2)
"""
从前往后 每一个元素都要跟其后面的其他元素作比较
如果出现左大右小 则进行交换
"""
def selection_sort(arr):
for i in range(len(arr) - 1): # 少一轮
for j in range(i + 1, len(arr)):
if arr[i] > arr[j]:
arr[i], arr[j] = arr[j], arr[i]
arr = [5,2,3,1,4]
selection_sort(arr)
print(arr)
(2)冒泡排序

# 冒泡 O(n^2)
"""
从前往后 元素之间两两进行比较
如果左大右小则交换
"""
def bubble_sort(arr):
# 0 1 2 3
for i in range(len(arr) - 1): #-1 少一轮
for j in range(len(arr) - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
arr = [5,2,3,1,4]
bubble_sort(arr)
print(arr)
(3)插入排序
# 选择 O(n^2)
def insertion_sort(arr):
# 从第2个元素开始遍历
for i in range(1, len(arr)):
j = i
while j > 0 and arr[j - 1] > arr[j]:
arr[j - 1], arr[j] = arr[j], arr[j - 1]
j -= 1
arr = [5,2,3,1,4]
insertion_sort(arr)
print(arr)
根据循环的特性来去解决特定的问题,而不是学习循环本身,学算法思想!
循环之间的好坏其实也有区别,主要在于数据的分布情况
(1)大致升序
(2)大致降序
(3)趋于稳定(方差小,相等值比较多)
(4)完全随机
用time模块记录一下运行时间
