2025妈妈杯数学建模B题完整分析论文

2.1 问题1分析

针对问题1，构建优化的搬迁补偿建模。

本问的解题思路围绕搬迁补偿方案设计与多因素影响分析展开：首先基于地块租金价值（题目包含：南北向15元/㎡/天、东西向8元/㎡/天）构建核心补偿模型，通过“面积补偿公式”平衡原地块与迁入地块的租金价值，结合朝向差异设定采光补偿规则（如南北向迁东西向追加20%面积补偿），并明确修缮补偿弹性范围（0-20万元/户）；同时考虑布局（独门独户/多户混居）、心理价位（情感补贴、社区服务）等配套补偿策略。其次，识别影响搬迁的额外因素，定量层面包括距街道距离（噪音补偿）、周边建筑密度（采光遮挡补偿）、通勤成本（时间补贴），定性层面涵盖社会关系网络（集中搬迁）、政策透明度（公示机制）、产权顾虑（法律咨询）、时间损失（过渡房安置）等，针对..........

2.2 问题2分析

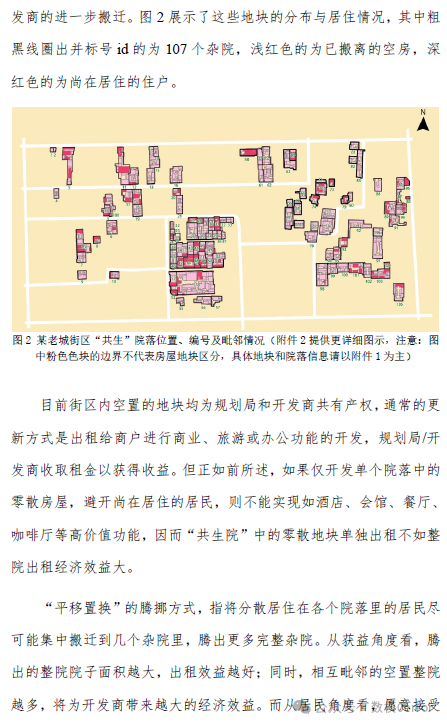
针对问题2，首先依据附件 1 筛选住户数≤5户的院落，结合附件二锁定 76、98、103、105 号潜在毗邻院落，其中 76 号天然空置，优先搬迁 98 号（1 户）、103 号（5 户）、105 号（2 户）以腾空院落；迁入地块遵循 “同院落 / 毗邻空置地块优先” 原则，降低通勤成本与面积补偿压力（如 98 号住户迁入同院落北向空置地块，租金等价无需补偿）。搬迁补偿基于问题一的租金价值模型，对不同朝向差异计算面积补偿（如 103 号东向住户迁入西向地块，按租金差 15→8 元 /㎡/ 天及舒适度调整系数 1.1 计算补偿面积），同步控制沟通（3 万元 / 户）与修缮成本（0-20 万元 / 户，取均值 15 万元）。腾退后形成 4 个毗邻完整院落（76、98、103、105 号），总面积 3877㎡，......

2.3 问题3分析

针对问题3的解题思路围绕“十年期租金增量与搬迁成本的性价比阈值（m≥20）”展开，通过边际效益分析寻找拐点：首先构建性价比模型，其中租金增量为整院（含毗邻溢价）与原分散地块的租金差，成本包含单户固定成本（53万元/户）。按“住户数从少到多”排序院落，优先搬迁单户、双户院落（成本低、增益高），逐步纳入三户、四户院落，计算边际性价比。发现随着住户数增加，成本增速超过租金增益增速，当搬迁至“四户及以下院落”时，性价比 \( m \) 接近或等于20，形成临界状态：此时搬迁对象为所有住户数≤4的院落（覆盖113户中的约100户），腾出院落形成大规模毗邻集群（总面积70,000㎡），总成本约5300万元，十年租金增量达10.........

2.4 问题4分析

针对问题4的解题思路围绕“构建全流程自动化决策软件框架”展开，旨在通过参数输入、模块计算和算法支撑实现老旧街区平移置换的智能决策：首先定义人工输入参数，涵盖地块基础数据（ID、院落ID、面积、朝向、住户状态）、补偿规则（租金单价、单户成本、调整系数）、规划目标（预算、周期、性价比阈值）及区位环境因素（街道距离、建筑密度等），为模型计算提供基础数据。其次设计核心计算模块：数据预处理模块通过院落聚类、住户统计和毗邻关系图构建，形成“地块-院落-毗邻”网络；问题二决策引擎按“住户数从少到多”筛选目标院落，优先匹配同院落或毗邻院落空置地块，利用图论算法扩展毗邻集群，动态优化搬迁组合以最大化整院面积与毗邻效益；问题三计算引擎构建租金增益模型（搬迁前后租金差）和成本累加模型，通过边际........

↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓