当前位置：首页 > news >正文

6.6.图的广度优先遍历(英文缩写BFS)

news 来源：原创 2025/4/19 13:15:35

树是一种特殊的图，树的广度优先遍历即层次遍历，所以会从树的角度入手图的广度优先遍历：

BFS与DFS的区别在于，BFS使用了队列，DFS使用了栈

一.广度优先遍历：

1.树的广度优先遍历：

详情见"5.13.树和森林的遍历"

2.图的广度优先遍历：

以上述图片为例，从2号结点出发，开始图的广度优先遍历，首先访问2号结点：

通过2号结点可以找到下一个与之邻近的结点即1号结点和6号结点，并访问1号结点和6号结点：

之后分别从1号结点和6号结点出发，再找到与他们邻近的下一个结点并进行访问，通过1号结点找到下一个与之邻近的结点即5号结点并访问5号结点，通过6号结点找到下一个与之邻近的结点即3号结点和7号结点，并访问3号结点和7号结点：

再分别从5号结点、3号结点和7号结点出发，分别找到下一个与之邻近的结点，可知5号结点已经没有与之邻近的下一个结点，通过7号结点可以找到与之邻近的下一个结点即4号结点和8号结点，并访问4号结点和8号结点，3号结点只能找到下一个与之邻近的结点即4号结点并访问4号结点：

二.对比树和图的广度优先遍历：

1.遍历结点：

无论是树，还是图，在进行广度优先遍历时，都需要通过某一个结点找到与之相邻的其他结点，只有实现了这个操作，才可以一层一层往下找到所有的结点：

对于树而言，要找到与某一个结点相邻的其他结点，只需要找该结点的孩子即可；

对于图而言，找相邻的结点只需要通过下述图片的基本操作即可（详情见"图的基本操作"）：

2.搜索结点：

上述图片所示，

对于树而言，由于各个结点之间的路径不存在"回路"，因此通过树里的某一个结点搜索其他结点时，搜索到的一定是某个结点的孩子即搜索到的结点一定是之前没有访问过的结点；

对于图而言，由于图中存在环路，而且像上述图片里的无向图，每一条边不存在方向，比如首先访问2号结点，通过2号结点可以搜索到6号结点，通过6号结点，可以找到2、3、7号结点，又或者通过3号结点可以找到4号结点，通过7号结点也可以找到4号结点，此时4号结点就被访问过两次，所以需要对这种情况进行处理->此时只需要对各个结点进行一个标记，标记一个结点是否被访问过，如果访问过，下一次如果搜索到被访问的结点，就跳过这个被访问过的结点即可->这样就可以保证在遍历时每个结点只访问一次。

上述图片所示，

实现树的广度优先遍历的时候，需要队列的帮助，因为虽然用肉眼来看，与2号结点同层的3、4号结点一眼就可以找到，但对于计算机而言结点却只能一个一个处理这些结点，暂时还没有处理的结点就需要用一个队列存储起来。

类似的，如上述图片所示，

实现图的广度优先遍历，也可以设置一个队列，此时有3个问题：

1.需要找到与某一个指定顶点相邻的所有顶点，可以利用"图的基本操作"中提到的两个操作(找第一个邻接点，找后一个与之相邻接的顶点)；

2.标记哪些顶点被访问过，只需要定义一个布尔类型数组来标记每一个顶点是否被访问过；

3.需要一个辅助队列；

图的广度优先遍历的代码实现如下：

visited[MAX_VERTEX_NUM]中的MAX_VERTEX_NUM就是图中顶点最大个数
visited数组初始值都设为false，代表一开始所有顶点都没有被访问过，数组的下标都是从0开始，但此时给出的例子中编号是从1开始，所以数组从1索引开始操作，0索引就保持false不动
BFS函数的形参v和形参G，表示从第v号顶点出发，遍历图G，Graph是图的类型，在"图的存储结构-邻接矩阵法"中有提到
visit函数代表访问顶点，传入v表示访问图G中第v号顶点；visited数组表示第v号顶点是否被访问过，visited[v]=true表示图G中第v号顶点被访问过
Enquene函数的作用是把数据添加到队列中，Q是队列，数据类型为SqQueue，详情见"队列的顺序实现"，v代表第v号顶点，Enqueue(Q,v)就是把第v号顶点添加到队列Q中
while循环的循环条件是判断队列Q是否为空，isEmpty函数的作用用来判断队列Q是否为空，为空的话返回true，不为空的话返回false，如果队列Q不为空，!isEmpty(Q)的结果为true，此时执行while循环
while循环中，DeQueue的作用是让队列Q中第v号顶点即队头元素出队，然后队头指针指向下一个元素，接下来要操作出队的第v号顶点->首先要通过第v号顶点找到与第v号顶点相邻的所有顶点，这个操作可以通过while循环里的for循环实现，其中FirstNeighbor(G,v)用来找第v号顶点在G中的第一个邻接点，若存在该邻接点，返回该第一个邻接点的编号，赋值给w，如果w非负，执行for循环，首先判断是否执行if语句，若符合条件!visited[w]为true即第w号顶点没有被访问过，那么就执行if语句，先访问第w号顶点，再把第w号顶点对应的数组的值修改为true，然后第w号顶点进入队列Q，该层for循环结束，再执行NextNeighbor(G,v,w)函数，第w号顶点是第v号顶点的第一个邻接点，找除了第w号顶点外第v号顶点的的下一个邻接点，找到了返回该邻接点的顶点号，赋值给w，判断是否非负，若非负，执行for循环，如不是非负即小于0，跳出for循环->for循环结束后需要判断是否执行下一层while循环，之后以此类推，执行完while循环，图G的广度优先遍历结束
FirstNeighbor(G,v)函数和NextNeighbor(G,v,w)函数就是用来找邻接点的，然后返回邻接点的序号，对于这两个函数如何找邻接点，有什么不同，详情见"图的基本操作"

3.图的广度优先遍历实例：

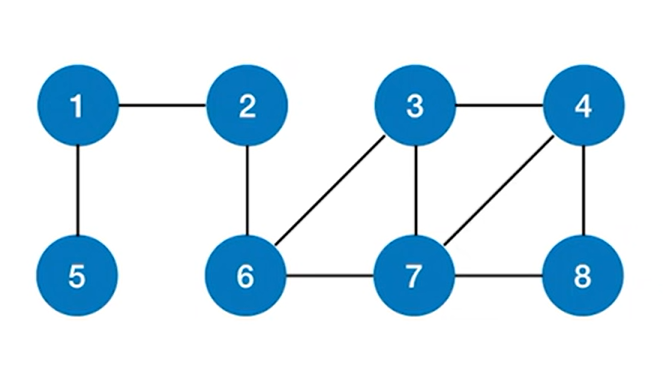
例如使用广度优先遍历，遍历上述图，

下述图片的代码之前有详解：

如上述图片所示，假设首先访问2号顶点，修改2号顶点对应的visited数组里的值为true，之后2号顶点入队，此时队头指针指向2号顶点，执行while循环，调用isEmpty函数判断Q队列是否为空（为空的话isEmpty函数返回true，不为空的话isEmpty函数返回false），显然不为空，!isEmpty(Q)的结果为true，执行while循环体->

如上述图片所示，调用DeQueue函数让2号顶点即队头顶点出队，开始操作2号顶点，通过for循环找到与2号顶点相邻的所有顶点->

如上述图片所示，最终会找到与2号顶点相邻的1号顶点和6号顶点，1号顶点和6号顶点都没有被访问过，所以会执行if语句，调用其中的visit函数、修改visited数组中的值，而且访问过的顶点即1号顶点和6号顶点还需要放到对应的队列的尾部即执行EnQueue函数->

如上述图片所示，for循环结束后，就访问完和2号顶点相邻的所有顶点即处理完2号顶点->

如上述图片所示，会再次判断是否执行while循环，此时2号顶点已出队，队列里只剩1号顶点和6号顶点，而且队头顶点是1号顶点，当前队列不为空，意味着执行while循环，首先调用DeQueue函数把队头指针指向的1号顶点出队，然后执行for循环找与1号顶点相邻的所有顶点，与1号顶点相邻的顶点有2号顶点和5号顶点，由于2号顶点在visited数组中对应的值为true，意味着2号顶点被访问过，所以不满足if语句，因此不会再操作2号顶点，但对于5号顶点，由于5号顶点对应的数组的值为false，符合if语句，因此会访问5号顶点，并且修改5号顶点对应数组的值，并把5号顶点入队尾，至此，1号顶点处理完毕，开始处理下一个顶点即进行下一层while循环->

如上述图片所示，当前队列不为空，因此执行while循环->

如上述图片所示，队头元素为6号顶点，调用DeQueue函数让6号顶点出队，执行for循环找和6号顶点相邻的所有顶点，和6号顶点相邻的顶点有2、3、7号顶点，2号顶点已经被处理过，所以只会处理3、7号顶点，3、7号顶点会入队，这样就处理完6号顶点->

如上述图片所示，同理开始处理5号顶点->

如上述图片所示，5号顶点出队，5号顶点相邻的只有1号顶点，1号顶点已经被处理过，所以不执行if语句，5号顶点处理完毕->

如上述图片所示，同理处理3号顶点，3号顶点出队列，与3号顶点相邻的顶点有4、6、7号顶点，其中只有4号顶点没有被访问过，所以访问4号顶点，修改4号顶点对应的数组的值，把4号顶点放入队尾，3号顶点处理完毕->

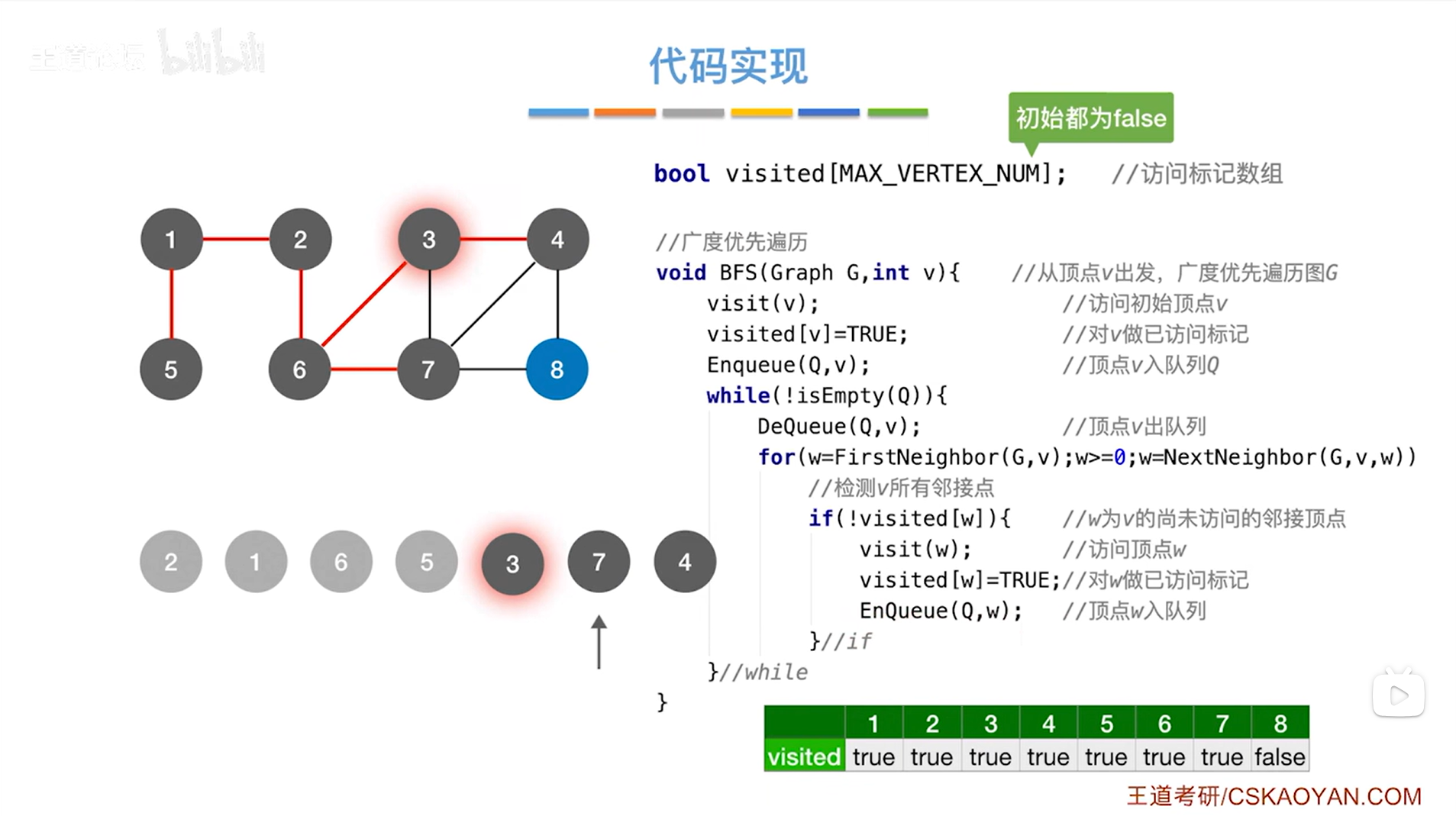
如上述图片所示，同理处理7号顶点->

如上述图片所示，7号顶点出队，7号顶点与3、4、6、8号顶点相邻，只有8号顶点没有被访问过->

如上述图片所示，所以访问8号顶点，修改8号顶点对应的数组的值，把8号顶点放入队尾，7号顶点处理完毕->

如上述图片所示，以此类推，接下来会依次操作队列里的4号顶点和8号顶点，由于和他们相邻的所有的顶点都已经处理完毕，所以4、8号顶点的for循环是不会执行的->

完成了该图的广度优先遍历，最终得出的遍历序列如下图所示：

4.图的广度优先遍历的遍历序列具有可变性：

如上述图片所示，从不同顶点出发遍历同一张图，得到的遍历序列是不同的。

对于上述图片中，从顶点3开始广度优先遍历图，与顶点3相邻的分别是4、6、7号顶点，其中顶点序号是按照递增的顺序来的->

事实上，对于广度优先遍历算法，如果图的存储结构不一样，从一个顶点出发，那么找到与之相邻的顶点的顺序也可能不一样：

如果图使用邻接矩阵存储，图的邻接矩阵的表示方式是唯一的，所以如果图使用邻接矩阵来存储，要找到和3号顶点相邻的其他顶点的话，找到的顶点的序号就固定依次是4、6、7号->顺序固定
如果图是用邻接表存储，那么最终查找邻接点的顶点号结果就可能不一样，如上图，从2号顶点出发，和2号顶点相邻的两个顶点的顺序可以是先找到1号顶点，再找到6号顶点，也可以是先找到6号顶点，再找到1号顶点，因为邻接表中顶点对应的链表的存储结构没有先后之分->顺序不固定

所以在图的广度优先遍历中，如果图采用邻接表存储的话，那么最终的遍历序列就是不唯一的；如果图采用邻接矩阵存储的话，由于邻接矩阵的表示方式唯一，那么最终的遍历序列也是唯一的。

5.图的广度优先遍历算法存在的问题以及解决方案：

如上述图片所示，其中的图任意两个顶点都是连通的，所以是连通图，从任何一个顶点出发，都能遍历完所有顶点，但存在一些问题->

以下述图片为例，该图中相较于上述图片里的图，增加了3个顶点即第9、10、11号顶点，这3个顶点与其他顶点不连通，此时存在两个顶点之间不连通，此图为非连通图，从某一个顶点出发，是无法遍历完所有顶点的：

从2号顶点出发遍历上述图片的图，通过上述图片里的代码是无法访问到第9、10、11号顶点的，那这个该怎么处理呢？

在visited数组中，这个数组记录了所有顶点是否已经被访问，那我们在第一次调用BFS函数之后，其实可以检查一下在visited数组当中能不能找到值为false的顶点，如果能找到，那就从该顶点出发，再调用一次BFS函数即可，此时就可以把没访问的顶点访问完，所以改进方案如下：

对于上述图片里的代码，增加了一个BFSTraverse函数，该函数的解读如下：

BFSTraverse函数的形参Graph G是图
vexnum是图G的顶点个数，G.vexnum代表图G中的顶点个数
第一个for循环中visited[i]=false就是初始化visited数组，都赋值为false，代表图G中的顶点都没有被访问过
InitQueue(Q)函数用来初始化辅助队列Q，Q是队列，详情见"队列的顺序实现"
第二个for循环用来扫描visited数组中是否有值为false的数据，如果有，那么就会执行if语句再次调用BFS函数，从当前visited数组中值为false对应的顶点开始遍历

以上述图片为例，执行到BFSTraverse函数的第二个for循环时，第一个值为false的顶点为1号顶点（注：这里是从1号顶点开始，但BFSTraverse函数里的两个for循环都是从0开始，这个不用管，只需要知道他们都是从第一个开始即可），此时从1号顶点出发，调用BFS函数进行图的广度优先遍历，最终可以把1、2、3、4、5、6、7、8号顶点都访问完，因为这些顶点是连通的：

访问完1、2、3、4、5、6、7、8号顶点后，BFS函数第一次调用结束，此时1、2、3、4、5、6、7、8号顶点对应的visited数组里的值都变为true，第一次调用完BFS函数之后，for循环会继续往后找，判断是否需要再次调用BFS函数，此时的第9号顶点对应的visited的值为false，所以再次调用BFS函数，从9号顶点出发，最终通过9号顶点可以把剩下的9、10、11号顶点全部访问完，最终图全部遍历完毕，for循环结束，BFSTraverse函数结束：

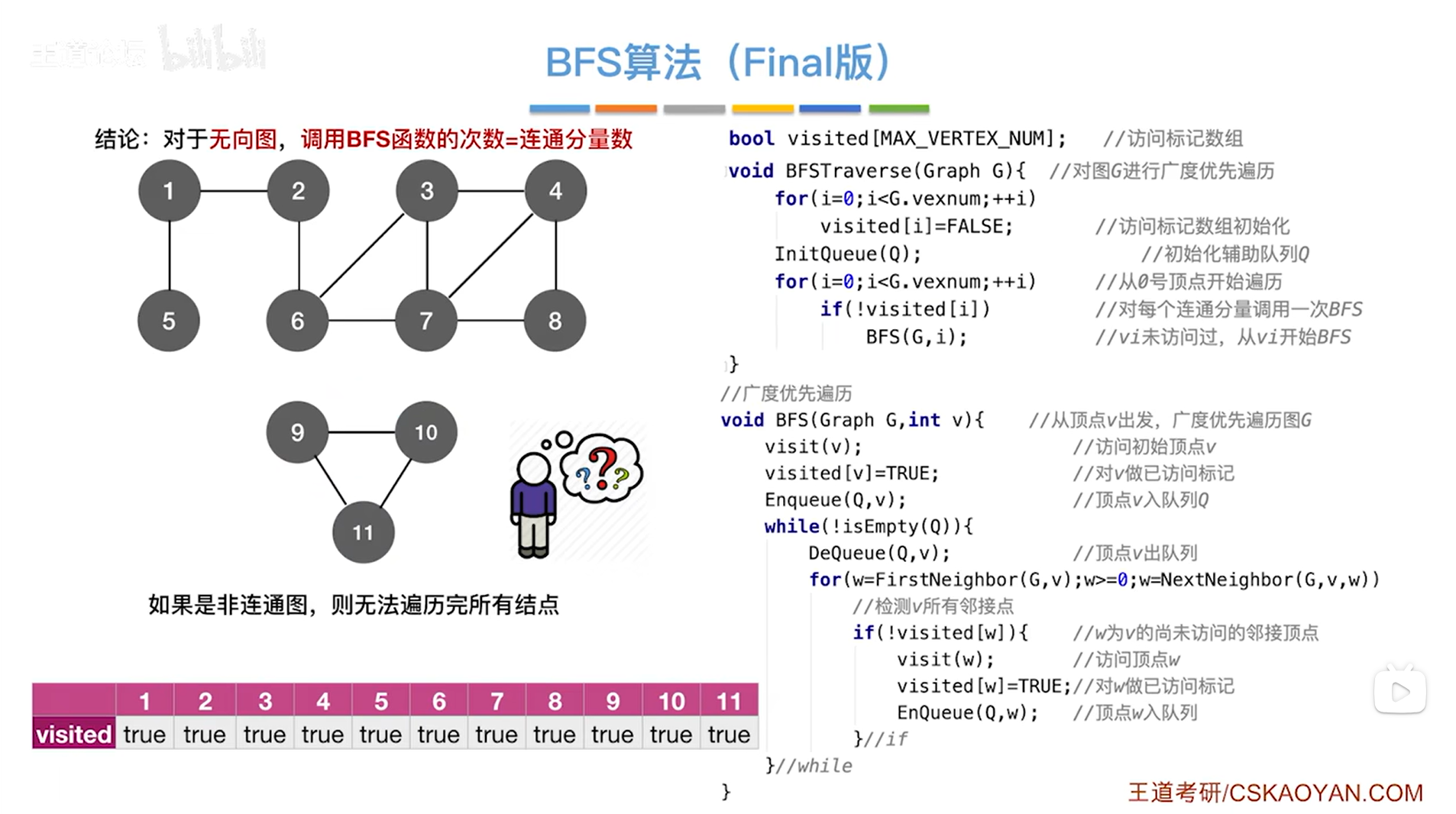
所以加上BFSTraverse函数里的第二个for循环之后，就可以遍历完非连通图里的所有顶点，总共调用了两次BFS函数。

结论：对于无向图，调用BFS函数的次数=连通分量数（连通分量数就是极大连通子图的个数，上述图片中，图的极大的连通子图分别由1、2、3、4、5、6、7、8号顶点组成和9、10、11号顶点组成，也就是有两个极大连通子图，所以连通分量数为2->找极大连通子图可以先把图的连通子图列出来，再找极大的）

三.图的广度优先遍历算法的效率：时间复杂度和空间复杂度

1.空间复杂度：

主要来自于定义的辅助队列InitQueue(Q)，因为队列里存顶点。

最坏的情况取决于辅助队列最大会有多少->

以上述图片为例，从1号顶点出发遍历图，显然除了1号顶点外所有顶点都和1号顶点邻接，所以在访问1号顶点时，同时要把和1号顶点相邻的所有顶点都放入辅助队列中，假设图中有V个顶点，那么辅助队列的最坏的情况就是需要O( |V-1| )个数量级，等价于O( |V| )。

2.时间复杂度：

在遍历图时，需要调用BFS函数里的visit函数遍历每一个顶点，同时在BFS函数里的for循环里还需要探索每一条边即找邻接点，所以可以简化的认为该算法的时间开销主要就是访问各个顶点和探索每一条边。

a.使用邻接矩阵存储图时：

假设图中有V个顶点，那么访问|V|个顶点就需要O( |V| )的时间（因为要用到循环），

当访问某个顶点时，还需要探索与该顶点相邻接的所有顶点，对于邻接矩阵，要找到和某一个顶点相邻接的所有顶点，只能把该顶点对应的一整行(或一整列，因为此时是无向图，无向图的邻接矩阵具有对称性)都遍历一遍，一整行总共有|V|个元素，

所以在找某一个顶点的邻接点时需要O( |V| )的时间，此时总共有|V|个顶点，因此找图中所有顶点的邻接点总共需要的时间复杂度为O( |V| * |V| )，

又因为要访问某个顶点，需要O( |V| )的时间，所以图使用邻接矩阵存储时，进行广度优先遍历的时间复杂度为O( |V| * |V| )+O( |V| ) ，等价于O( |V| * |V| )，其中V是图的顶点总数。

b.使用邻接表存储图时：

假设图中有V个顶点，那么访问|V|个顶点就需要O( |V| )的时间（因为要用到循环），

当访问某个顶点时，还需要探索与该顶点相邻接的所有顶点，对于邻接表，找到和某一个顶点邻接的所有顶点，只需要遍历该顶点对应的链表即可，因此邻接了多少个顶点即共有多少条边，就需要多少时间，

对于无向图来说，假设图中有E条边，在无向图的邻接表中，由于一条边有两个顶点，所以边顶点的个数是2|E|，所以要访问无向图的邻接表中某个顶点的所有邻接点（这个过程也是找和某个顶点邻接的所有边，是等价的，其中可能关于图中的所有边），总共需要的时间消耗为O( 2|E| )，等价于O( |E| )，

因此，当图使用邻接表存储时进行广度优先遍历，由于需要O( |V| )的时间复杂度进行顶点的访问，需要O( |E| )的时间复杂度进行对各个边进行访问即查找邻接点，因此图使用邻接表存储时，进行广度优先遍历的时间复杂度为O( |V| + |E| )，其中V是图的顶点总数，E是图的边总数。

注意：这里可以发现，在分析上述算法的时间复杂度时并没有像以前那样分析最深层的循环次数，为什么没有这么做呢？

举个例子，如果一个图的所有顶点之间都没有边相连，并且这个图是使用邻接表存储的话，

显然BFS函数里的for循环的循环次数就应该是0次（因为该for循环是找邻接点等价于找顶点连接的边，此时图中没有边），

在图的广度优先遍历中该图的每一个顶点都需要被访问，意味着每一次都需要调用BFS函数里的visit函数进行访问对应的顶点，假设图中有V个顶点，那么访问所有的顶点需要O( |V| )的时间复杂度，

但如果像以前那样只考虑最深层的循环次数是会出现问题的，因为此时最深层的BFS函数里的for循环一次也不执行（分析该for循环会导致时间复杂度为0，和实际的需要O( |V| )的时间复杂度不符），这个和算法的实现方式有关，

所以以后遇到分析图的广度优先遍历算法或者图的深度优先遍历算法的时间复杂度时，建议不要钻到代码里，就把问题简化->

记住图的广度优先遍历算法和图的深度优先遍历算法的时间开销都主要来自访问顶点和找各条边即找邻接点，所以只需要拆开来分析，访问各个顶点需要多长时间，访问各条边即找邻接点需要多长时间，结合具体的存储结构进行分析即可。

四.广度优先生成树：

1.实例：

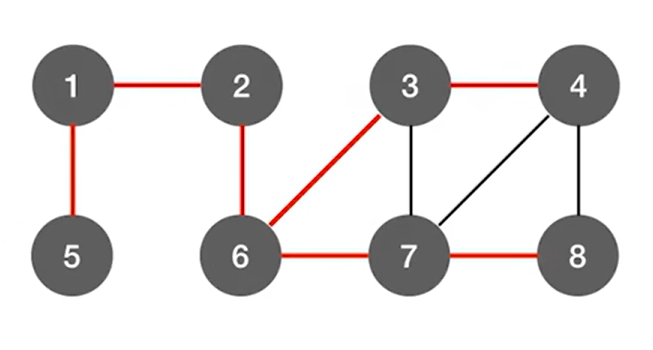
上述图片中标红的边意味着当某一个顶点第一次被访问的时候是从哪一条边过去的，

比如第一次访问4号顶点时，是从3号顶点过去的，而不是从7、8号顶点过去，

用这样的方式，如果图中有n个顶点，那么总共标红了n-1条边（上述图片中有8个顶点，此时标红了7条边），

如果只把红色的边留下，结果如下：

此时就变成了树，因为其中就不存在回路了，上述图片的树就是最终得出的广度优先生成树，

这个树是根据图的广度优先遍历的过程得来的。

再回顾一遍：

如下图，首先访问的是2号顶点：

如下图，和2号顶点相邻的顶点是1、6号顶点即通过2号顶点可以找到1、6号顶点，其中1号顶点先入队列，6号顶点后入队列：

如下图，通过1号顶点可以找到5号顶点，通过6号顶点可以找到3、7号顶点，通过邻接矩阵或邻接表中可以看出，通过顶点6往后找，找到没有访问的顶点中（2号顶点已经访问过了），应该先找到3号顶点，再找到7号顶点，所以3号顶点应该先入队，7号顶点后入队：

如下图，接下来通过3号顶点可以找到4号顶点，通过7号顶点可以找到8号顶点：

最终得到了广度优先生成树。

2.变式：

如上述图片的邻接表里，把顶点6对应的链表中3号和7号进行互换，结果如下：

如下图，从2号顶点出发开始访问：

如下图，根据2号顶点会找到1、6号顶点，1号顶点比6号顶点先入队：

如下图，通过1号顶点可以找到5号顶点，通过6号顶点可以找到7、3号顶点，在当前这个邻接表中找与6号顶点相邻的且没有被访问过的顶点应该是先找到7号顶点，再找到3号顶点，所以7号顶点比3号顶点先入队列->接下来首先要找的是和7号顶点相邻的且没有被访问过的顶点：

如下图，与7号顶点相邻的且没有被访问过的顶点是4、8号顶点，所以通过7号顶点可以找到4、8号顶点：

最终得到了该图的广度优先生成树。

3.分析实例与变式：

实例中得出的广度优先生成树和变式中得出的广度优先生成树是有区别的，原因在于：

用邻接表存储一个图时表示方式不唯一，因此得到的遍历序列也不唯一，从而得到的广度优先生成树也不唯一；

用邻接矩阵存储一个图时表示方式唯一，因此得到的遍历序列也唯一，从而得到的广度优先生成树也是唯一的。

五.广度优先生成森林：

实例：

如上图所示，该图是一个非连通图，其中有两个连通分量（连通分量就是极大连通子图的个数，上述图片中，图的极大的连通子图分别由1、2、3、4、5、6、7、8号顶点组成和9、10、11号顶点组成，也就是有两个极大连通子图，所以连通分量为2->找极大连通子图可以先把图的连通子图列出来，再找极大的），由这两个连通分量即由1、2、3、4、5、6、7、8号顶点组成的图和由9、10、11号顶点组成的图就可以得出广度优先生成森林，

由1、2、3、4、5、6、7、8号顶点组成的图可以得出一个广度优先生成树，

由9、10、11号顶点组成的图也可以得出一个广度优先生成树，

这两个广度优先生成树就可以组成广度优先生成森林。