DSA数据结构与算法 4

第2章 排序技术

2.1 排序简介

排序是将数据按照特定顺序（升序或降序）排列的过程，它不仅是计算机科学中的基础操作，也是日常生活中不可或缺的工具。举个例子，想象一个图书馆里的书籍，如果这些书籍没有按照作者的姓氏或书名的字母顺序排列，我们在寻找一本特定的书时将会面临极大的困扰，甚至可能根本找不到目标书籍。排序的作用就在于通过建立明确的顺序，使得大量数据在存储和访问时能够更加高效，减少搜索所需的时间和精力。

排序分为两种类型：

• 内部排序：如果要排序的数据能够一次性放入内存中，那么就是进行内部排序。
• 外部排序：当要排序的数据过大，不能一次性加载到内存时，这些数据会被存储在辅助存储器（如硬盘、软盘、磁带等）中，然后使用外部排序方法进行排序。

排序的应用

排序在许多应用中都非常有用，特别是在数据库应用中，可以根据需要对数据进行排序。例如：

1. 数据库应用中，排序用于将数据按照指定顺序排列。
2. 在字典类应用中，数据需要按字母顺序排列。
3. 排序也有助于从一组元素中快速搜索目标元素。
4. 检查元素的唯一性时，排序也能提供帮助。
5. 在某些算法中，寻找最接近的一对数据需要排序。

2.2 排序技术

1. 冒泡排序
2. 插入排序
3. 基数排序
4. 快速排序
5. 归并排序
6. 堆排序
7. 选择排序
8. 希尔排序

2.2.1 冒泡排序

冒泡排序的核心思想是：通过逐一比较数组中相邻的两个元素，如果前面的元素比后面的元素大，就交换它们的位置。这个过程会继续进行，直到没有需要交换的元素为止。冒泡排序得名于元素像气泡一样“浮”到列表的顶端。通过这种方法，经过一轮排序后，最大的元素会被移到数组的末尾。

值得注意的是，如果要将元素按降序排列，那么在第一轮排序中，最小的元素将被移到数组的最高位置。

例子：

假设我们有一个数字数组 A[] = {30, 52, 29, 87, 63, 27, 19, 54}，我们可以将其看作一群人在排队等候时，按照身高（数值大小）进行排序。每次比较两个相邻的人，如果前一个人的身高比后一个人高，那么他们就交换位置。每一轮结束后，身高最高的人就像气泡一样“浮”到队伍的最后。

这种方式的好处是，虽然每次只移动少数元素，但最终会将所有元素按正确的顺序排列。冒泡排序的时间复杂度是$O(n^2)$，因此当数据量较大时，它的效率较低。对于小规模数据，冒泡排序足够有效，但对于大规模数据集，通常需要更高效的排序算法。

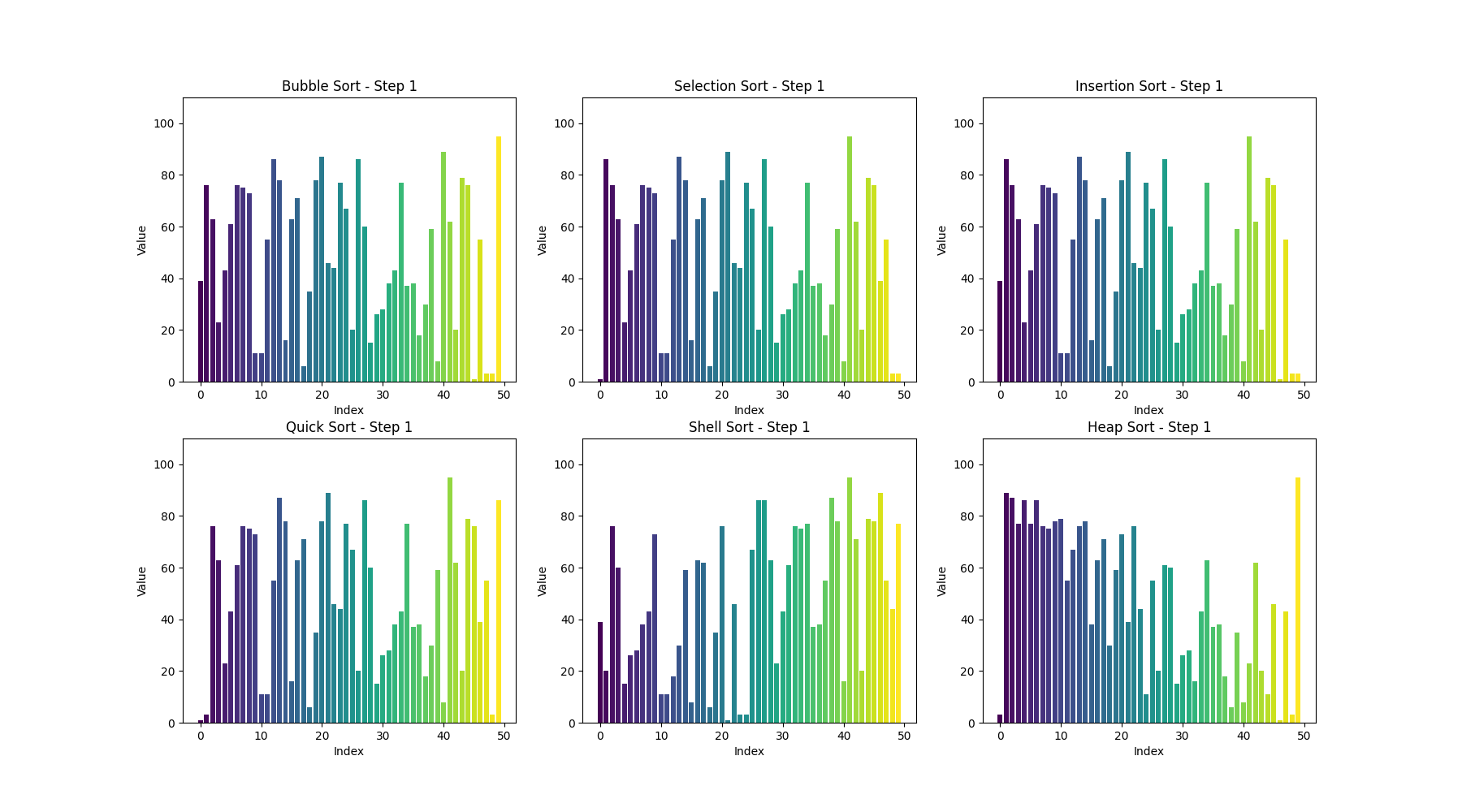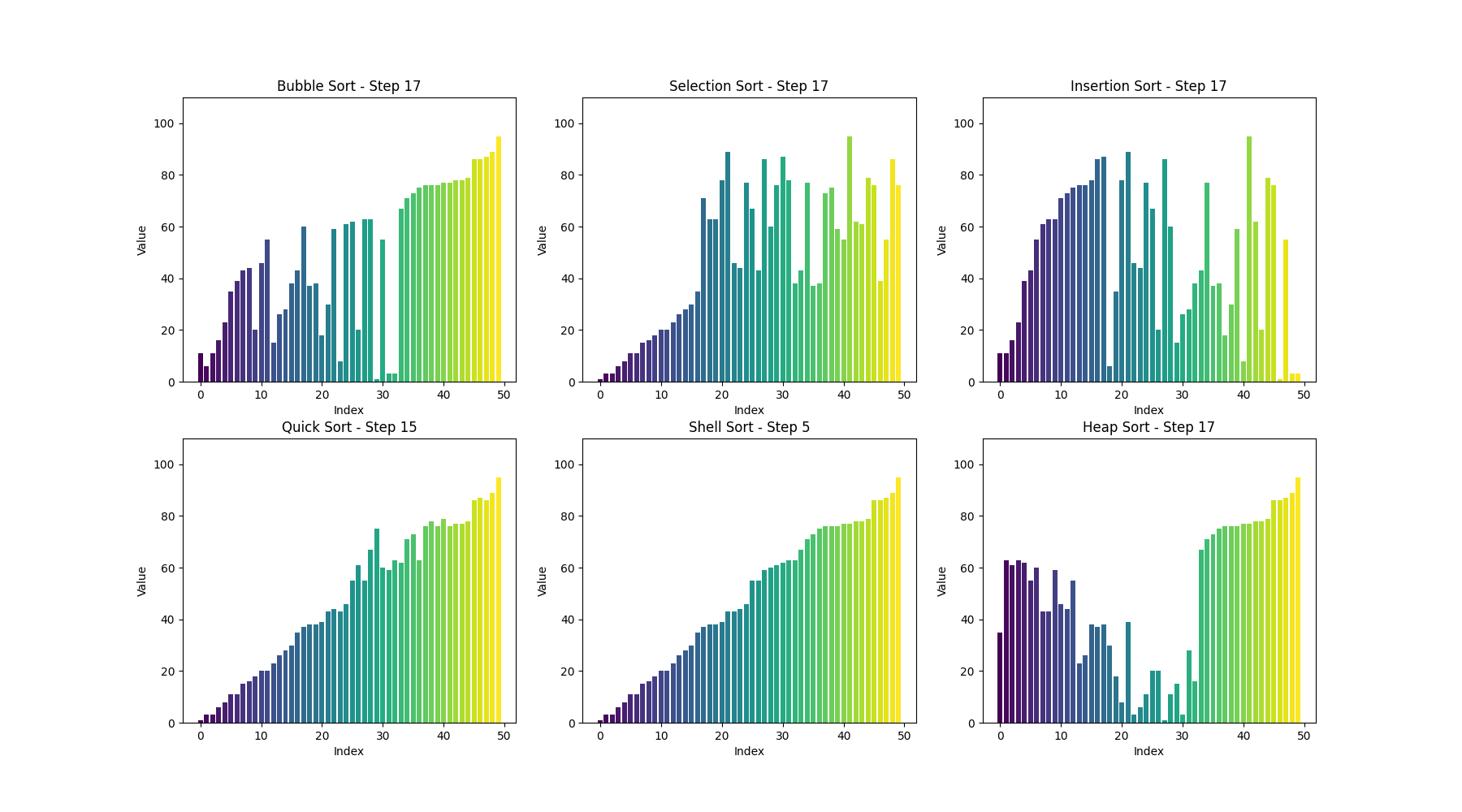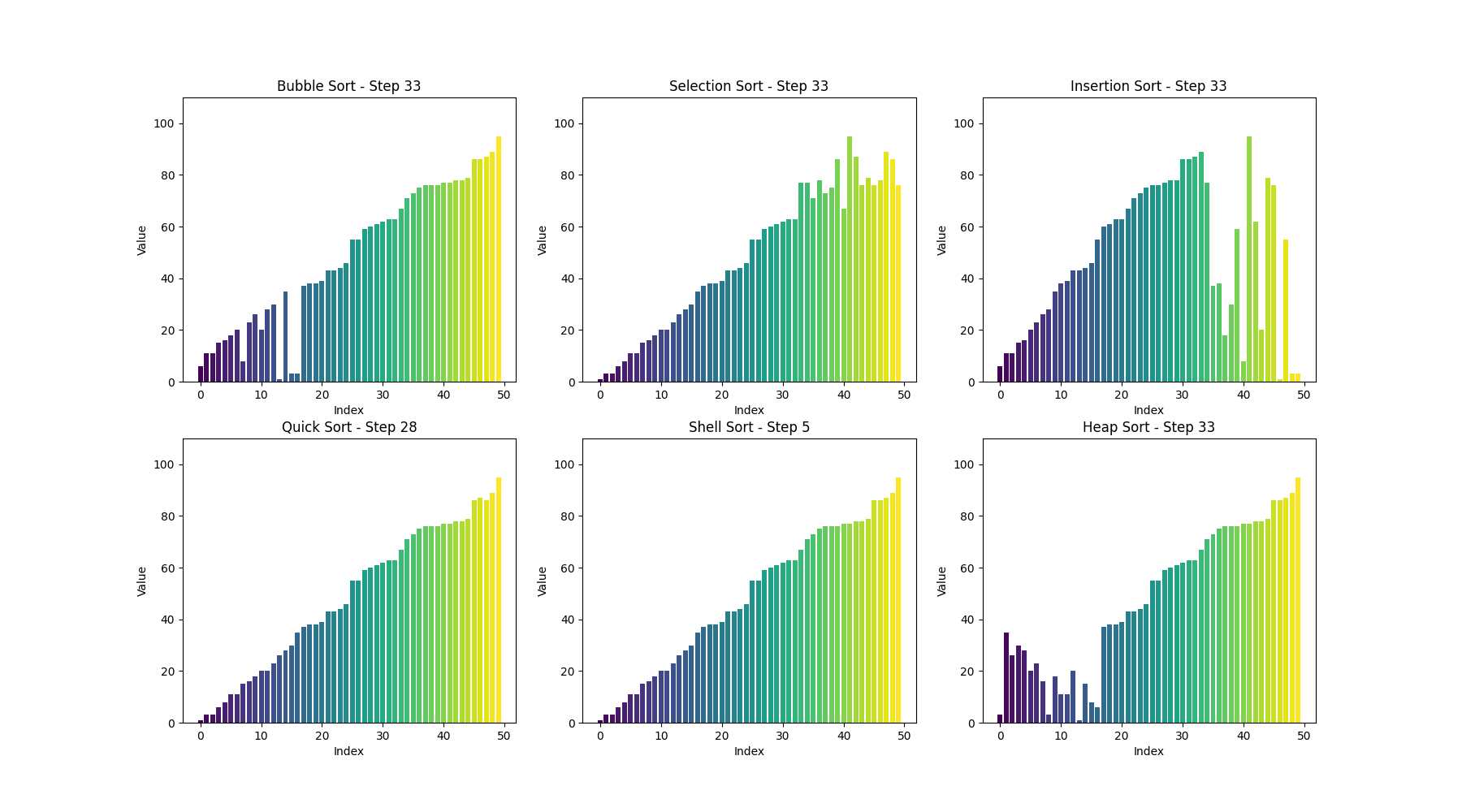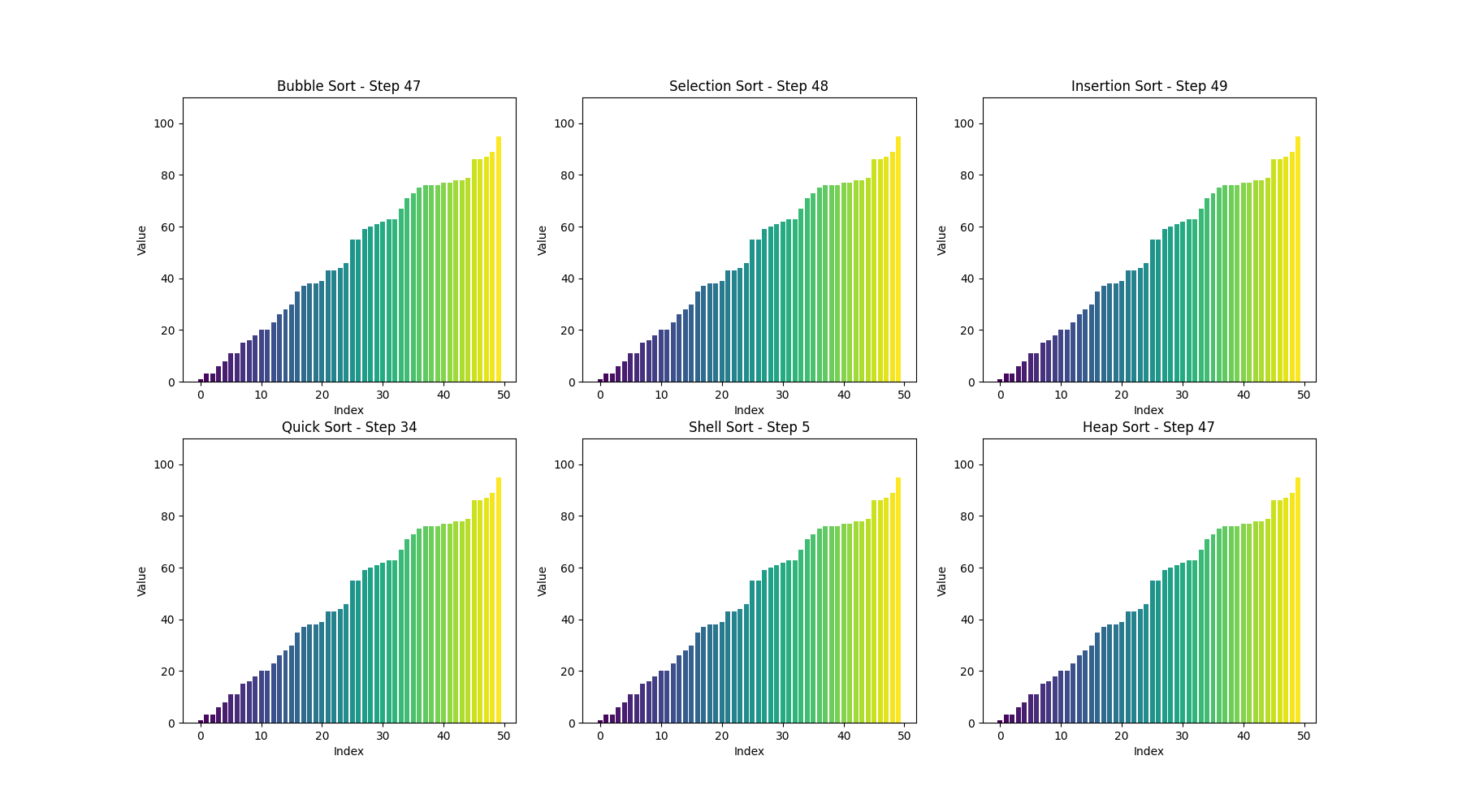
可视化bubble sort

def bubble_sort(arr):n = len(arr)# 用于存储每一步的数组状态steps = []# 外层循环，控制排序的趟数for i in range(n):swapped = False  # 标记是否发生了交换for j in range(0, n-i-1):if arr[j] > arr[j+1]:arr[j], arr[j+1] = arr[j+1], arr[j]  # 交换元素swapped = Truesteps.append(arr.copy())  # 保存每一步的状态# 如果一趟排序没有交换任何元素，说明数组已经有序，提前结束if not swapped:breakreturn steps

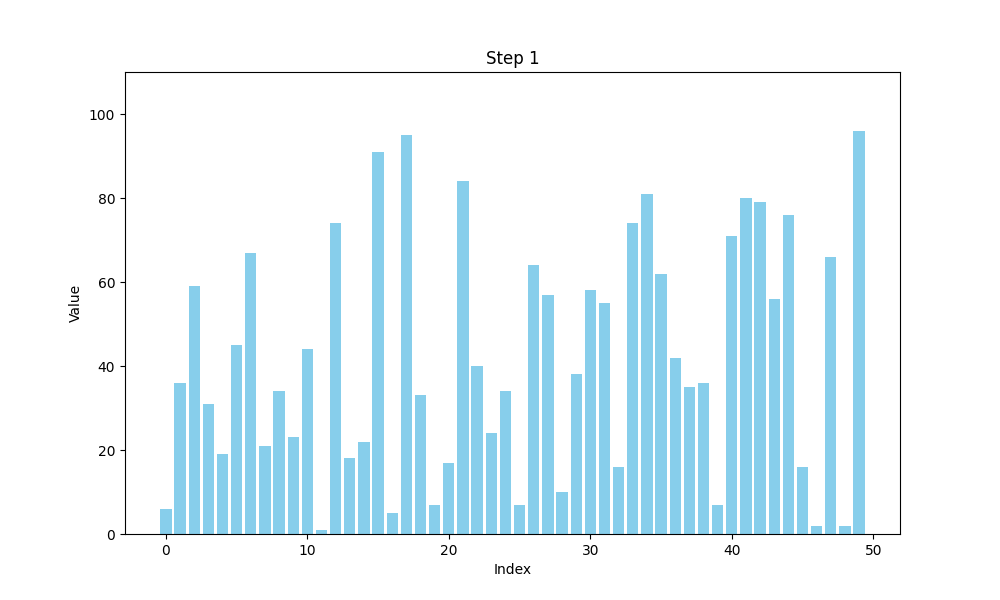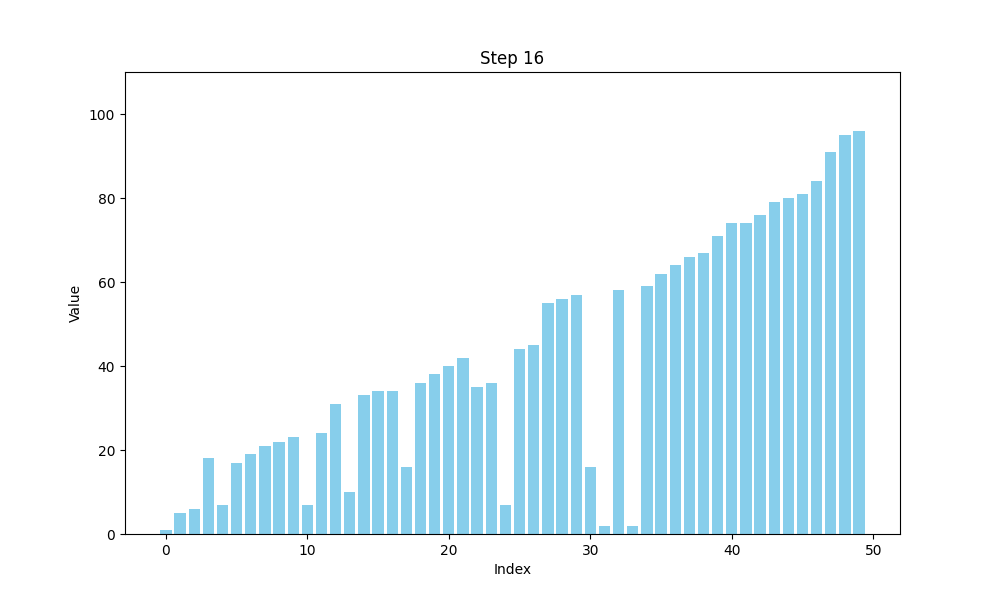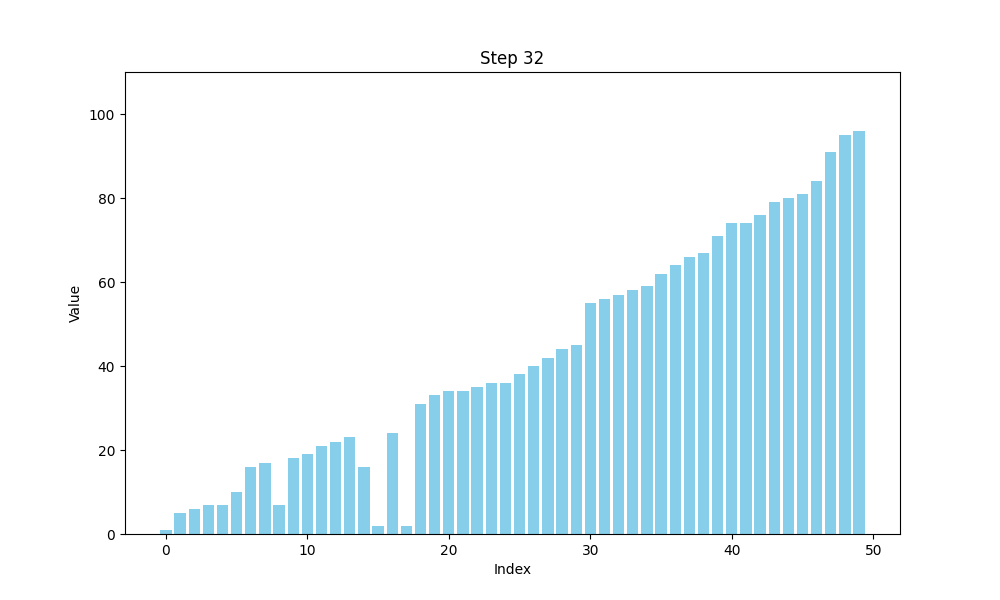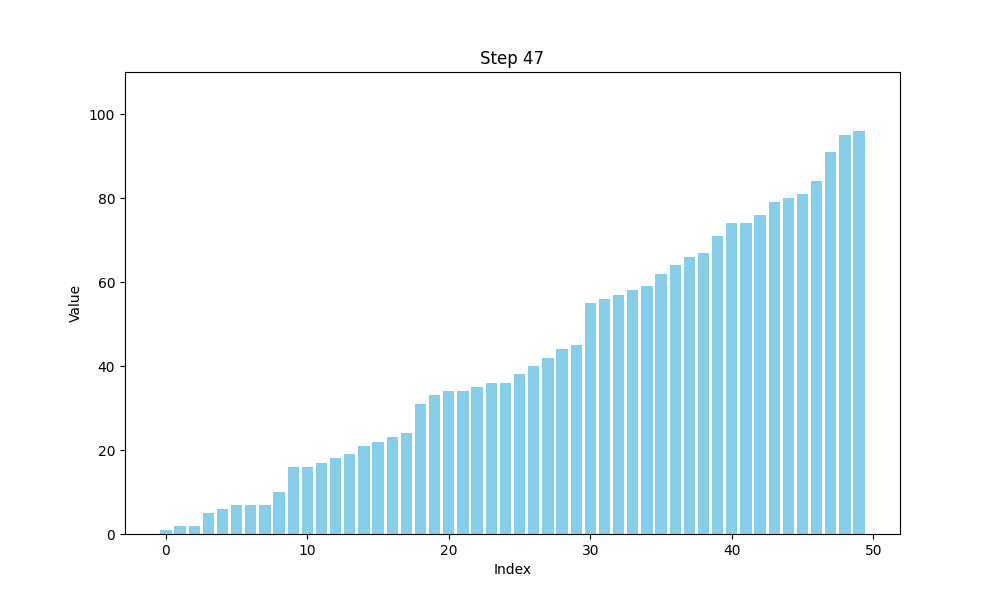
冒泡排序的时间复杂度分析

排序算法的复杂度通常与比较次数密切相关。冒泡排序的时间复杂度也不例外。我们可以通过分析冒泡排序中的比较次数来得出其复杂度。

冒泡排序的核心思想是通过不断比较相邻的元素，如果前面的元素比后面的元素大，则交换它们的位置。经过每一轮比较后，最大的元素逐步“浮”到列表的末尾。可以理解为，冒泡排序就像一个逐步筛选出最大元素的过程，每一轮都会将一个最大的元素“冒”到最顶端。

假设我们有一个包含 $n$ 个元素的数组。冒泡排序的过程可以分为 $n-1$ 轮比较。具体来说：

• 第一轮：需要进行 $n-1$ 次比较，将最大的元素“冒”到最后一个位置。
• 第二轮：剩余的 $n-1$ 个元素中，再进行 $n-2$ 次比较，将第二大的元素放到倒数第二个位置。
• 以此类推，直到第 $n-1$ 轮，只剩下两个元素进行一次比较。

因此，冒泡排序的比较次数总和为：

$$f(n)=(n-1)+(n-2)+(n-3)+\cdots +2+1$$

这个求和可以简化为：

$$f(n)=\frac{n(n-1)}{2}$$

进一步展开这个公式，我们可以得到：

$$f(n)=\frac{n^2}{2}+O(n)$$

其中 $O(n)$ 表示在最坏情况下的线性时间消耗，通常可以忽略不计。因此，冒泡排序的时间复杂度是：

$$O(n^2)$$

这意味着，随着元素数量 $n$ 的增加，冒泡排序的执行时间会按 $n^2$ 的比例增长。换句话说，元素数量翻倍时，冒泡排序所需的时间将增加四倍。这也说明了冒泡排序在处理大规模数据时效率较低。

比喻

想象你正在整理一堆乱放的书，每本书上都有一个编号。在每一轮整理中，你从头到尾检查两本相邻的书，确保它们按照编号顺序排列。如果发现有一本编号较大的书排在了前面，你就交换它们的位置。每完成一轮整理，你就确定了一本最大的书在正确的位置。这样，你需要重复 $n-1$ 次整理，才能确保所有书本按顺序排好。

这就像冒泡排序一样，每一轮比较和交换会“将”最大的元素移动到正确的位置。整个过程需要多轮排序，每一轮减少了一个需要排序的元素。最终，所有元素都排好了顺序。

---

插入排序（Insertion Sort）

插入排序是一种非常简单的排序算法，它通过逐个将元素插入到已排序好的数组（或列表）中，来完成排序的过程。我们对这种排序方法并不陌生，实际上，当我们玩扑克牌时，通常会使用这种排序技巧。比如在打桥牌时，我们需要将手中的牌按照大小排序，插入排序就是一种非常直观的方式。

插入排序的基本思想是将每一个元素插入到其在已排序部分中的正确位置。在第一次迭代中，插入排序将第一个元素与第零个元素进行比较；在第二次迭代中，将第二个元素与第零个和第一个元素进行比较，依此类推。在每次迭代中，当前元素都要与前面的所有元素进行比较，直到找到其适合的位置。总之，插入排序的每一步都将当前元素插入到已排序部分的正确位置。

举例

假设我们有一个数组，需要使用插入排序对其进行排序：

23, 29, 11, 1

在第一轮迭代中，23 和 29 比较，23 已经是正确的位置；接着，29 与 23 比较；之后，再将 11 插入已排序部分，逐个元素与前面的元素进行比较，最终插入到正确的位置。

可视化插入排序

# 插入排序算法
def insertion_sort(arr):n = len(arr)# 用于存储每一步的数组状态steps = []# 从第二个元素开始，逐一插入到已排序部分for i in range(1, n):key = arr[i]  # 当前要插入的元素j = i - 1# 找到key元素的插入位置while j >= 0 and arr[j] > key:arr[j + 1] = arr[j]  # 将比key大的元素右移j -= 1arr[j + 1] = key  # 将key插入到正确的位置steps.append(arr.copy())  # 保存每一步的状态return steps

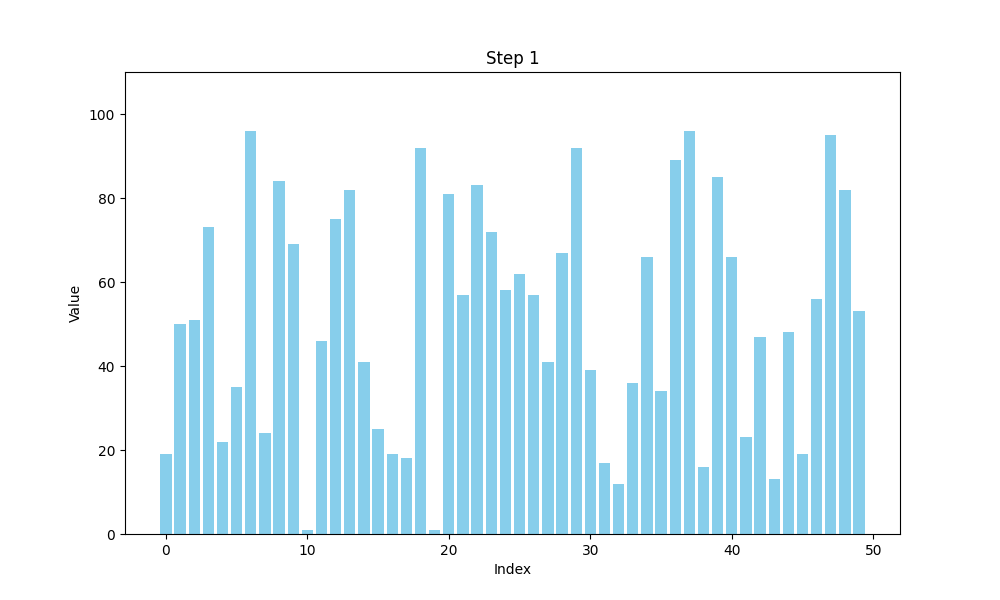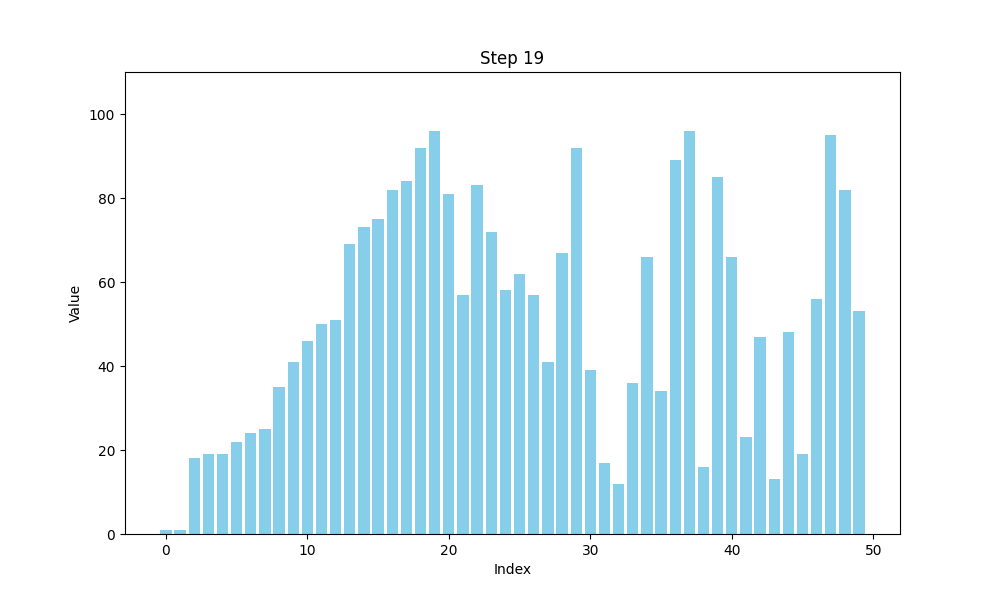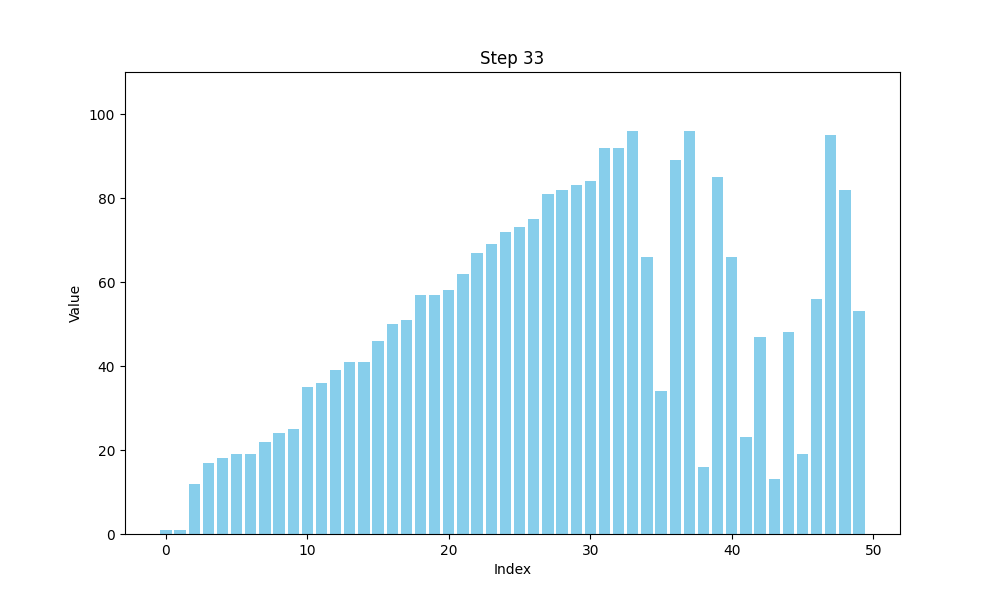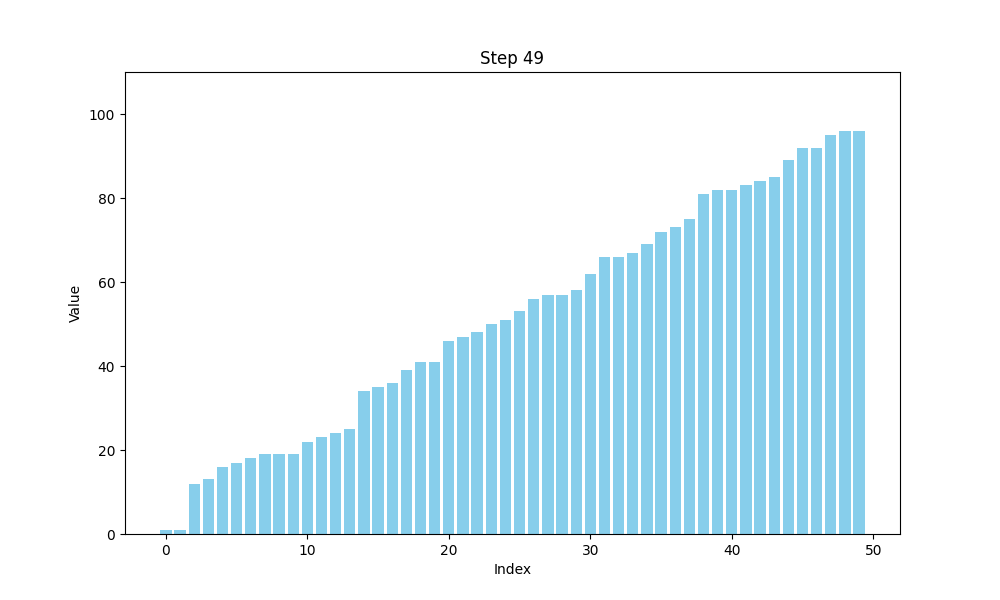
插入排序的时间复杂度

如果初始数组已经是排序好的，那么每一次迭代中仅需要进行一次比较，因此排序的复杂度是 $O(n)$，即线性时间。然而，如果初始数组是完全逆序的，最坏情况下，复杂度就会达到 $O(n^2)$。

最坏情况下，插入排序的比较次数总和为：

$$(n-1)+(n-2)+\cdots +3+2+1=\frac{(n-1)\ast n}{2}$$

这就意味着最坏情况的时间复杂度是 $O(n^2)$。

平均情况下，插入排序的比较次数也接近 $O(n^2)$，因为每次都可能需要进行多次比较才能找到合适的位置。因此，插入排序的平均时间复杂度也是 $O(n^2)$。

比喻

我们可以将插入排序想象成整理一个乱序的扑克牌堆。你手里有一副散乱的扑克牌，每次从手里拿出一张新牌，然后将它插入到已经排序好的部分。你会从已经排序的牌堆中，逐一比较新牌和已排序牌堆中的牌，直到找到一个位置，把这张新牌插入其中。随着你不断进行这个过程，最终你会将所有牌都整理成有序的状态。

这就像插入排序一样，每次从未排序部分取出一个元素，将其插入到已排序部分的合适位置。整个过程逐渐构建起一个有序的序列。

---

选择排序（Selection Sort）

选择排序是最简单的排序算法之一。它的基本思想是：首先找到数组中最小的元素，并将它与第一个位置的元素交换；接着找到第二小的元素，并将其与第二个位置的元素交换，依此类推，直到整个数组被排序完成。通过这种方式，选择排序逐步将最小的元素放到已排序部分的末尾，直到所有元素都有序。

选择排序的过程

选择排序的操作可以理解为在每一轮排序中，选择一个最小的元素并将其放到正确的位置。每一轮的操作就像是挑选一个元素，放到最前面的位置，剩下的元素继续重复此过程。我们可以想象自己在整理一堆书，每次从中找出一本最薄的书，放到书架的最前面，直到书架上的书全部按照从薄到厚的顺序排列。

def selection_sort(arr):n = len(arr)# 用于存储每一步的数组状态steps = []# 外层循环，控制排序的趟数for i in range(n):min_idx = i  # 假设当前元素为最小值for j in range(i+1, n):if arr[j] < arr[min_idx]:  # 找到更小的元素min_idx = j# 交换元素arr[i], arr[min_idx] = arr[min_idx], arr[i]steps.append(arr.copy())  # 保存每一步的状态return steps

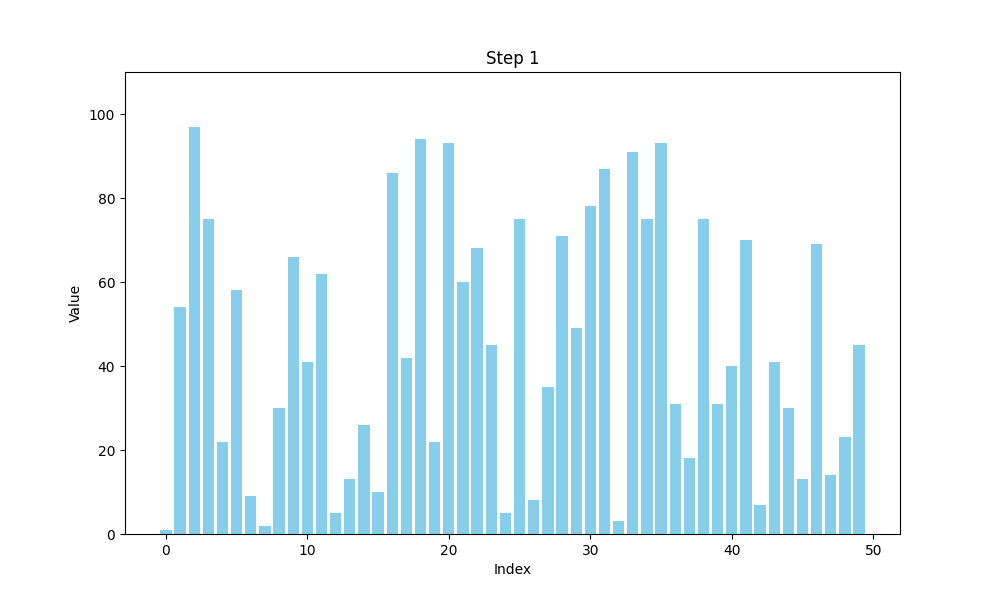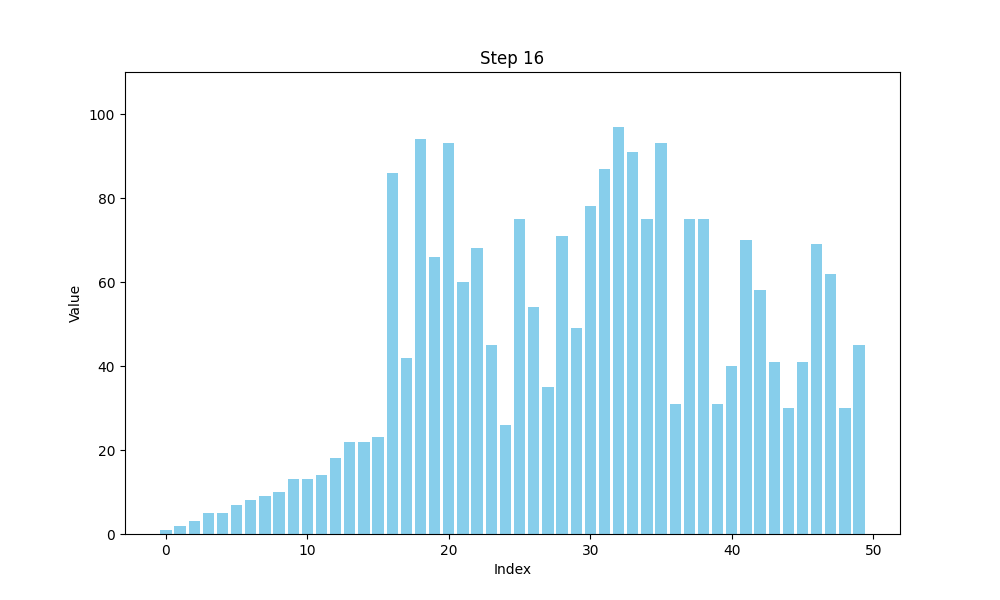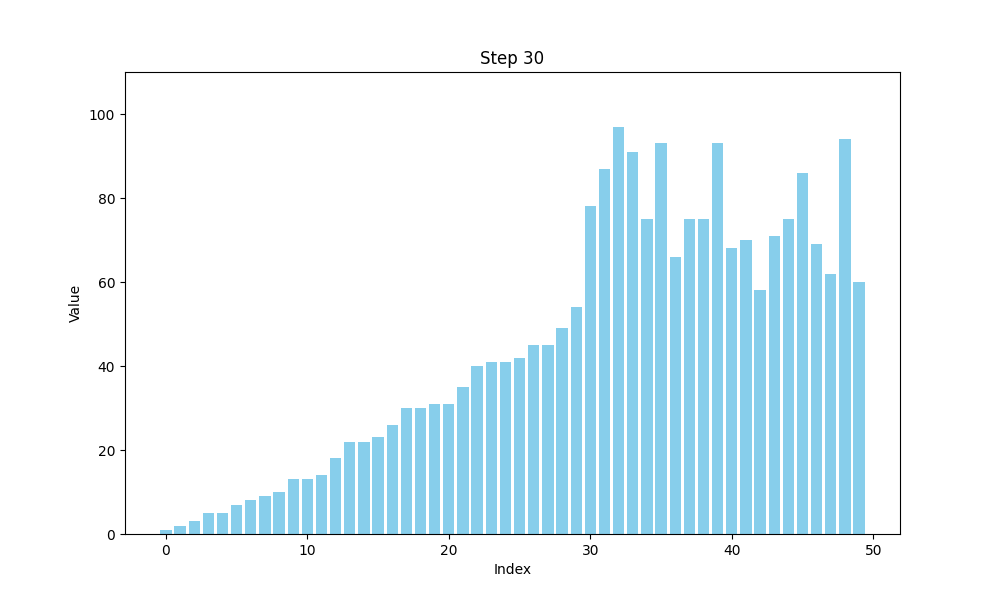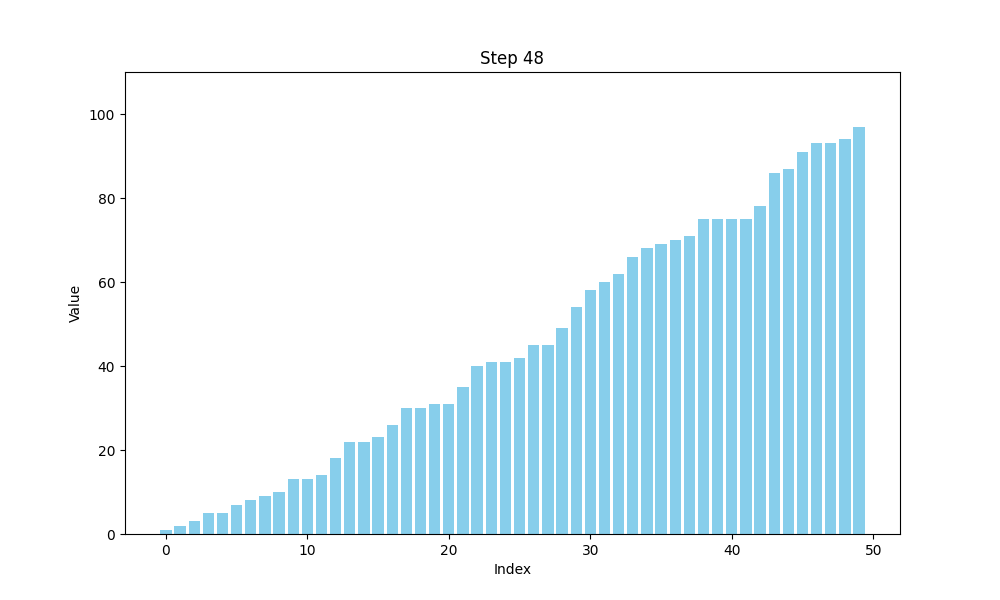
选择排序的时间复杂度

选择排序的时间复杂度可以通过比较次数来计算。假设我们有一个包含 $n$ 个元素的数组：

• 在第一轮中，第一个元素与剩余的 $n-1$ 个元素进行比较。
• 在第二轮中，第二个元素与剩下的 $n-2$ 个元素比较。
• 这个过程会一直持续，直到最后一个元素为止。

这些比较的次数可以用数学公式表示为：

$$(n-1)+(n-2)+\cdots +(n-(n-1))$$

这个求和可以简化为：

$$\frac{n(n-1)}{2}$$

这意味着选择排序的比较次数是与 $n^2$ 成正比的，因此它的时间复杂度为：

$$O(n^2)$$

这表明，随着元素数量的增加，选择排序的执行时间将按 $n^2$ 的比例增长。换句话说，当元素数量翻倍时，排序所需的时间将增加四倍。

比喻

我们可以将选择排序比作挑选和整理书架上的书。想象你有一堆乱七八糟的书，目标是按照书的厚度从薄到厚排列好。每次你都会从中挑选出一本最薄的书，然后将它放到书架的最前面。接着，你继续在剩下的书中挑选出最薄的一本，放到第二个位置，直到所有书都排列好。每一次挑选书的过程就像是在寻找最小的元素，并将其放到正确的位置，这样逐步完成整个排序过程。