MATLAB 控制系统设计与仿真 - 39

多变量系统控制器设计实例2

假如原系统对象中有位于虚轴上的极点，则不能直接应用鲁棒控制设计来设计控制器。

在这样的情况下，需引入一个新的变量p，使得

即可在对象模型中用p变量取代s变量，这样的变换称为双线性变换，还称为频域平面双线性变换。

在双线性变换下，可以将原系统中虚轴上的极点移开，这样就可以将这个模型用作新的对象模型，基于这个模型设计一个控制器。

假设已经设计出一个控制器K(p),还应引入变换

将得出的控制器中的p变量再变回到s变量，从而获得新的控制器Kc.

MATLAB鲁棒控制工具箱中提供了bilin函数来完成给定传递函数模型的正向或反向双线性变换。函数的调用格式为：

GT = bilin(G,VERS,METHOD,AUG); % VERS= 1, forward transform% VERS=-1, reverse transform% Method 请参考下图 

假设带有双积分器的非最小相位受控对象为：

选择加权函数

设计最优控制器，绘制校正后系统的闭环阶跃响应。

MATLAB代码如下：

clear all;clc;
s=tf('s');
G=5*(-s+3)/s^2/(s+6)/(s+10);
W1=300/(s+1);
W2=10^(-5);
W3=100*s^2;
p1=-1;
p2=-100;
G0=ss(G);
Gs=bilin(G0,1,'Sft_jw',[p1 p2]); % bilinear pole shifted plant Gt
Gaug=augtf(Gs,W1,W2,W3);
[Kt,CL,gamma]=hinfsyn(Gaug);
K =bilin(Kt,-1,'Sft_jw',[p1 p2]); % final controller K
figure(1)
step(feedback(G*K,1)); % closed loop system response
title('closed loop system response')
grid on;
figure(2)
step(feedback(G,K)); % closed loop controller output
title('closed loop controller output')
grid on;

程序运行结果如下：

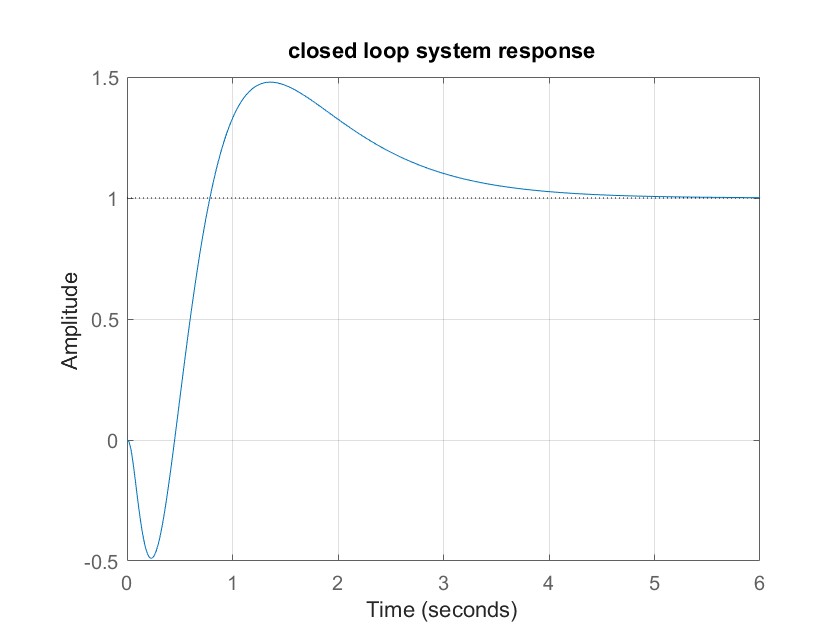
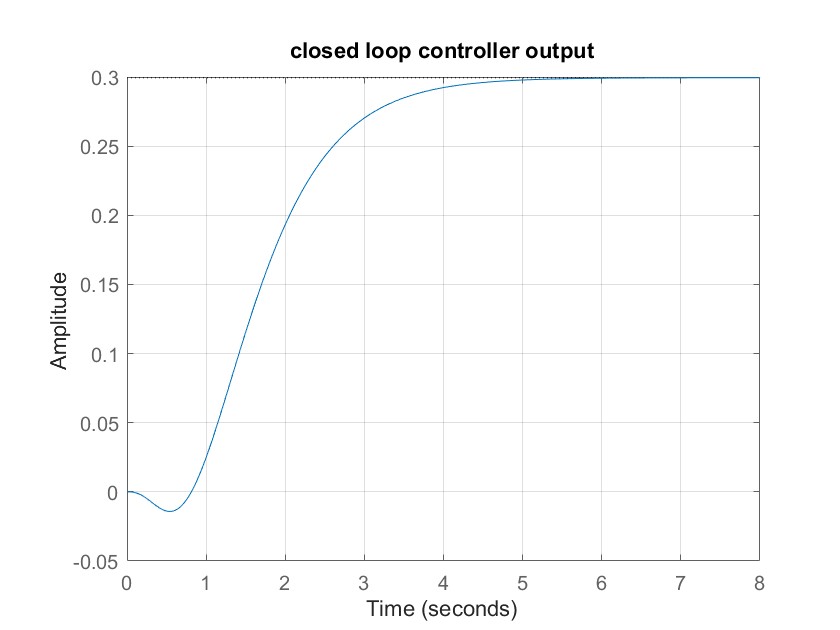
然后我们可以加入下面MATLAB代码，查看原系统G0和新系统Gs的零极点位置

figure(3)
pzmap(G0)
hold on
pzmap(Gs)
title('zero/pole shift')
legend('G0','Gs')

程序运行结果如下：

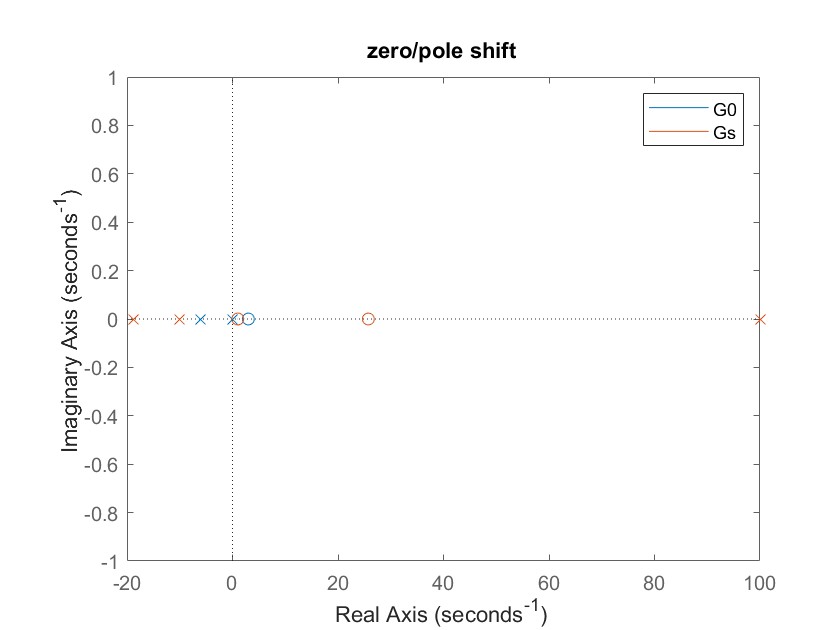
最后，欢迎大家有问题给我留言。

非常感谢小伙伴们的-点赞-收藏-加关注。