当前位置：首页 > news >正文

卷积神经网络基础（二）

news 来源：原创 2025/4/22 14:56:00

停更好久的卷积神经网络基础知识终于开始更新了哈哈，今天主要介绍的是误差反向传播法。

一、计算图

1.1 用计算图求解

1.2 局部计算

1.3 为什么采用计算图

二、链式法则

2.1 计算图的反向传播

2.2 链式法则

2.3 链式法则和计算图

三、反向传播

3.1 加法节点反向传播

3.2 乘法节点反向传播

3.3 苹果的例子

一、计算图

误差反向传播法是一种高效计算权重参数梯度的方法，可以通过基于数学式和基于图的两种方法学习，前者较为常见，在这里主要介绍基于图的方法。

这里说的图指得是数据结构图，就是包含若干结点和边（连接结点的线）的图。

1.1 用计算图求解

首先我们看这样一个问题：

一个苹果100日元，我现在买了两个苹果，苹果的消费税是10%，那么我最终的支付金额是多少？

结果就是 100×2×（100%+10%）=220日元。

图中我们将乘数 ×2 和 ×1.1 标注在⭕内，我们也可以仅仅将符号 × 标注在其中，而将数值2和1.1单独作为一个变量标注在外，就像这样：

这样我们就把苹果的个数和消费税单独标注在外了。

下面，问题变得更复杂：我不仅买了两个100日元的苹果，我还买了三个150日元的橘子，消费税仍为10%，我最终支付的金额是多少？

用第二种标注方法表示上述的问题可以得到这样的图：

这里我们新增了一个 + 的符号用来合并苹果和橘子原本的金额，最后与消费税相乘得到最终金额。这样我们就得到了最终的计算图。计算方式为从左向右，计算结果也从左边向右边传递，类似电流流动。最终答案就是715日元。

综上，采用计算图解决问题的流程如下：

构建计算图
在计算图的基础上，从左向右计算

从左向右计算是正方向的传播，我们称为“正向传播”（forward propagation），正向传播是从计算图出发点到结束点的传播。当然，也存在反向的传播（从右向左），这种传播称为“反向传播”。

1.2 局部计算

计算图的特征都是通过“局部计算”得到的，即与自己相关的某个领域内进行计算，而与全局的信息无关。

例如，我买了两个苹果和很多其他的东西，此时的计算图如下：

这里计算购买苹果所需的金额200与其他东西所需金额的4000如何计算得来没有任何关系，只关心苹果的个数和价格等。那么，计算图只用专注于局部计算即可，无论全局计算多么复杂，每个步骤仅需对对象节点完成局部计算。虽然局部计算很简单，但需要通过传递计算结果得到最终复杂的全局计算结果。

1.3 为什么采用计算图

那么，我们为什么采用计算图呢？计算图有什么优点呢？

首先，我们知道计算图只需考虑局部计算，这就让计算变得简单，从而简化问题。另外，计算图可以保存中间的计算结果，例如计算到两个苹果时金额为200日元，消费税之前的金额为4200日元等等。第三，计算图最大的优点就是可以通过反向传播高效计算导数。

我们重新考虑第一个问题：

我现在想知道，苹果价格的上涨会在多大程度上影响最终支付的金额，即求“支付金额关于苹果价格的导数”。设苹果价格为x，支付金额为L，相当于求 $\frac{\partial L}{\partial x}$ 。这个导数的意思就是苹果价格上涨时，支付金额会增加多少。

这个导数我们就可以通过计算图的反向传播来求出：

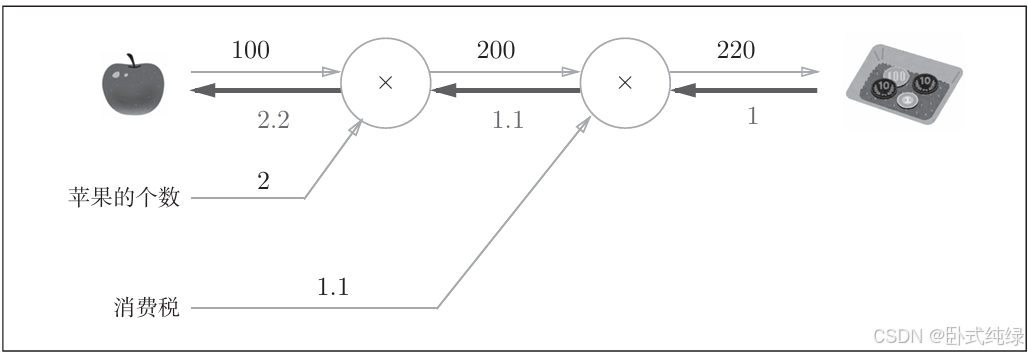
如图所示，我们用反向的神色箭头表示反向传播。从右向左传播的导数值分别为1——>1.1——>2.2，于是我们得知支付金额关于苹果价格的导数值为2.2，即苹果的价格每上涨1日元，支付的总金额就增加2.2日元。并且，我们在计算该导数的过程中，同样求出了支付金额关于消费税的导数以及支付金额关于苹果个数的导数，计算过程中的值都可以被共享。综上，计算图的优点就是通过正向和反向传播高效计算各个变量的导数值。

二、链式法则

我们经常接触到的计算都是从左至右的，而从右至左的反向传播可能会比较奇怪，其实这是基于链式法则的。

2.1 计算图的反向传播

这里我们看一个例子：

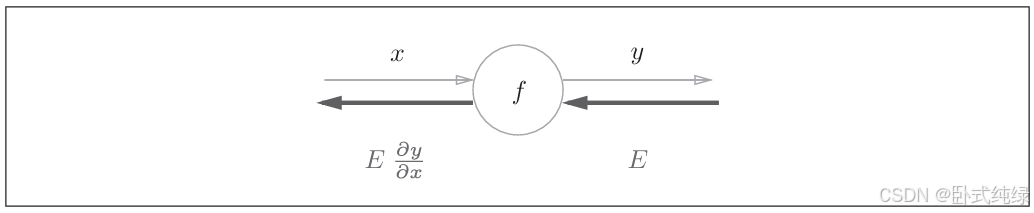
这里正向传播所表达的含义是一个关于x的函数y： $y=f(x)$ ,下面的反向箭头则表示反向传播。其传播顺序是：信号E乘以节点导数 $\frac{\partial y}{\partial x}$ 。这里的节点导数是指正向传播 $y=f(x)$ 的导数，比如 $y=x^{2}$ ,则 $\frac{\partial y}{\partial x}$ =2x，这样我们就可以高效求出导数的值了。