信息量、香农熵、交叉熵、KL散度总结

信息量

对于一个事件而言，它一般具有三个特征：

• 小概率事件往往具有较大的信息量

• 大概率事件往往具有较小的信息量

• 独立事件的信息量相互可以相加

比如我们在买彩票这个事件中，彩票未中奖的概率往往很高，对我们而言一点也不稀奇，给我们带来的信息量很小，彩票中大奖的概率往往非常低，中一次大奖则是非常罕见，给我们带来的信息量很大。

如何描述信息量大小呢？有如下定义：

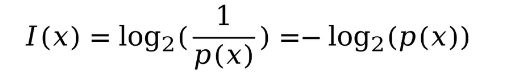
其中描述某一事件发生的概率，反映了信息量与发生概率之间成反比，取对数是为了 独立事件的信息量相互可以相加（第三个特征）。

有如下例子：

抛一枚硬币，根据正面朝上和反面朝上的概率计算其信息量

其中，当正反概率相等时，信息量对等；当正反概率不等时，概率越小的事件其信息量越大。

当我们对信息量这一概念有一个初步理解后，我们继续往下看关于熵的定义

 香农熵（Shannon Entropy）

熵：针对一个概率分布所包含的平均信息量

相当于计算一个概率分布中信息量的期望

由于熵这一概念是由科学家香农所提出，故熵又被称作香农熵（注意这里的熵与物理学中的熵不是同一个意思）。

 对于离散的概率分布，计算香农熵的公式如下所示：

 对于连续的概率分布，计算香农熵的公式如下所示： 

以离散的概率分布为例，我们可以看到，计算香农熵就是将每个事件的概率乘以其对应的信息量并进行向加求得。

我们同样回到抛硬币的例子：

计算每种情况的香农熵

 通过以上例子我们不难发现：

在一个概率分布中，当概率密度函数分布比较均匀的时候，随机事件发生的情况变得更加不确定，相应地，对应的熵更大；当概率密度函数分布比较聚拢的时候，随机事件发生的情况变得更加确定，相应地，对应的熵更小。

现在我们对熵的概念也有了一个基本的了解，我们继续往下看交叉熵。

交叉熵（Cross Entropy）

我们先不急着看概念，我们先看一个例子，同样是抛硬币的例子：

如果我们事先并不知道每个事件真实的概率p，我们可以先对其进行估计q，并计算在q下的信息量I，那我们可以计算在真实概率分布p下的平均信息量的估计，这个估计就称作交叉熵。

我们看一下交叉熵的公式（离散概率分布）：

连续概率分布交叉熵计算公式如下：

我们利用估计的信息量计算在真实概率下的熵便称为交叉熵。

根据上面的公式，我们计算一下在不同估计下的交叉熵：

从中我们可以发现，在不同估计下计算的交叉熵要大于香农熵（可以看下在之前在计算不同概率分布下的香农熵）。这是为什么呢？我们接着往下看。

KL散度（Kullback-Leibler Diergence）

一种定量衡量两个概率分布之间差异的方法：交叉熵与熵之间的差异。

如果理解了之前的熵和交叉熵，KL散度的定义也相对容易理解。

离散概率分布下的KL散度的计算公式如下：

离散概率分布下的KL散度的计算公式如下：

 

直观理解KL散度，可以看作在Q表示P所损失的信息量，KL 散度越大，说明 P和 Q的差异越大

KL散度有如下性质：

KL散度永远大于等于0 ，可通过吉布斯不等式证明。

这也就说明了为什么在不同估计下计算的交叉熵要大于等于香农熵，只有当p和q相等时，交叉熵才等于香农熵。

p和q交换后得出的KL散度不相等，因此KL散度不能看作距离，但可以用来优化模型

在机器学习中，如果想要优化一个模型，KL散度是一个重要的衡量标准，可通过最小化KL散度使模型最优。其中，在优化过程中，我们对其q进行梯度优化，由于p与q无关，故为0，最终梯度优化公式如下：