当前位置：首页 > news >正文

PaddlePaddle线性回归详解：从模型定义到加载，掌握深度学习基础

news 来源：原创 2025/4/23 8:31:46

前言
一、paddlepaddle框架的线性回归
1.1 paddlepaddle模型的定义方式
1.1.1 使用序列的方式 nn.Sequential 组网
1.1.2 使用类的方式 class nn.Layer组网
1.2 数据加载
1.3 paddlepaddle模型的保存
1.3.1 基础API保存
1.3.2 高级API模型的保存
1.3.2.1 训练fit进行保存
1.3.2.2 利用paddle.Model类进行保存
1.4 paddlepaddle模型的加载
1.4.1 基础API模型的加载
1.4.2 高级API加载
1.5 paddlepaddle模型网络结构的查看
1.5.1 summary
1.5.2 netron
1.5.3 visualdl
二、曲线拟合
1.1案例引入
1.2 散点输入
1.3 前向计算
1.4 Sigmoid函数引入
1.5 激活函数的引入
1.6 参数初始化
1.7 损失函数
1.8 开始迭代
1.9反向传播
1.10 梯度下降显示
1.11 曲线拟合代码
三、激活函数
3.1 激活函数及其导数算法理论讲解
3.2 激活函数的作用？
3.3 激活函数的概念
3.4 Sigmoid
总结

前言

书接上文

PyTorch与TensorFlow模型全方位解析：保存、加载与结构可视化-CSDN博客文章浏览阅读479次，点赞6次，收藏17次。本文深入探讨了PyTorch和TensorFlow中模型管理的关键方面，包括模型的保存与加载以及网络结构的可视化。涵盖了PyTorch中模型和参数的保存与加载，以及使用多种工具进行模型结构分析。同时，详细介绍了TensorFlow中模型的定义方式、保存方法、加载流程以及模型结构的可视化技术，旨在帮助读者全面掌握两大深度学习框架的模型管理技巧。https://blog.csdn.net/qq_58364361/article/details/147382076?spm=1011.2415.3001.10575&sharefrom=mp_manage_link

一、paddlepaddle框架的线性回归

从以下5个方面对深度学习框架paddlepaddle框架的线性回归进行介绍
1.paddlepaddle模型的定义
2.paddlepaddle模型的保存
3.paddlepaddle模型的加载
4.paddlepaddle模型网络结构的查看
5.paddlepaddle框架线性回归的代码实现
上面这5方面的内容，让大家，掌握并理解paddlepaddle框架实现线性回归的过程。
1.paddlepaddle 官网：https://www.paddlepaddle.org.cn/
安装
pip install paddlepaddle==2.6.2 -i https://mirror.baidu.com/pypi/simple

1.1 paddlepaddle模型的定义方式

主要针对基础API

1.1.1 使用序列的方式 nn.Sequential 组网

model=nn.Sequential(nn.Linear(1,1))

#导入库
import numpy as np
import paddle
import paddle.nn as nn
#设置随机数种子 ,保证结果可复现
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
# 2. 定义前向模型
# model=paddle.nn.Linear(1,1)#主要针对基础API
#方式1 使用序列的方式 nn.Sequential 组网
model=nn.Sequential(nn.Linear(1,1))# 3.定义损失函数和优化器
#3.1损失函数
criterion=paddle.nn.MSELoss()
#3.2 优化器
optimizer=paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
# 4.开始迭代
epochs=500
for epoch in range(1,epochs+1):#前向传播#unsqueeze()扩展一维y_prd=model(x_train.unsqueeze(1))loss=criterion(y_prd.squeeze(1),y_train)#清除之前计算的梯度optimizer.clear_grad()#自动计算梯度loss.backward()#更新参数optimizer.step()# 5.显示频率的设置if epoch % 10==0 or epoch==1:#可以使用float(loss)或者 loss.numpy()会报警告print(f"epoch:{epoch},loss:{float(loss)}")

1.1.2 使用类的方式 class nn.Layer组网

#导入库
import numpy as np
import paddle
import paddle.nn as nn
#设置随机数种子 ,保证结果可复现
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
#主要针对基础API
#方式 2 单独定义 使用类的方式 class nn.Layer组网
class LinearModel(nn.Layer):def __init__(self):super(LinearModel,self).__init__()self.linear=nn.Linear(1,1)def forward(self,x):x=self.linear(x)return x
# #定义模型的对象
model=LinearModel()# 3.定义损失函数和优化器
#3.1损失函数
criterion=paddle.nn.MSELoss()
#3.2 优化器
optimizer=paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
# 4.开始迭代
epochs=500
for epoch in range(1,epochs+1):#前向传播#unsqueeze()扩展一维y_prd=model(x_train.unsqueeze(1))loss=criterion(y_prd.squeeze(1),y_train)#清除之前计算的梯度optimizer.clear_grad()#自动计算梯度loss.backward()#更新参数optimizer.step()# 5.显示频率的设置if epoch % 10==0 or epoch==1:#可以使用float(loss)或者 loss.numpy()会报警告print(f"epoch:{epoch},loss:{float(loss)}")

1.2 数据加载

#1.先来看数据加载
#2.模型构建高层API#导入库
import numpy as np
import paddle
import paddle.nn as nn
from paddle.io import DataLoader,TensorDataset
#设置随机数种子 ,保证结果可复现
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
#TensorDataset是接收一个值，不是接收两个值,使用列表
dataset=TensorDataset([x_train.unsqueeze(1),y_train.unsqueeze(1)])
#创建Dataloader对象
dataloader=DataLoader(dataset,batch_size=10,shuffle=True)
# 2. 定义前向模型
#方式2 单独定义 使用类的方式 class nn.Layer组网
class LinearModel(nn.Layer):def __init__(self):super(LinearModel,self).__init__()self.linear=nn.Linear(1,1)def forward(self,x):x=self.linear(x)return x
#定义模型的对象
model=LinearModel()# 3.使用高层api进行封装
# step1 使用paddle.Model(xxx)进行封装
model=paddle.Model(model)
#step2 使用prepare
model.prepare(optimizer=paddle.optimizer.SGD(learning_rate=0.01,parameters=model.parameters()),loss=nn.MSELoss(),metrics=paddle.metric.Accuracy())
#step3启动训练
#需要用到数据，训练轮次 是否显示日志过程
model.fit(dataloader,epochs=500,verbose=1)

1.3 paddlepaddle模型的保存

1.3.1 基础API保存

按照字典的形式保存

paddle.save(model.state_dict(),'./基础API/model.pdparams')

#导入库
import numpy as np
import paddle
import paddle.nn as nn
#设置随机数种子 ,保证结果可复现
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
# 2. 定义前向模型
# model=paddle.nn.Linear(1,1)#主要针对基础API
#方式1 使用序列的方式 nn.Sequential 组网
# model=nn.Sequential(nn.Linear(1,1))#方式2 单独定义 使用类的方式 class nn.Layer组网
class LinearModel(nn.Layer):def __init__(self):super(LinearModel,self).__init__()self.linear=nn.Linear(1,1)def forward(self,x):x=self.linear(x)return x
#定义模型的对象
model=LinearModel()# 3.定义损失函数和优化器
#3.1损失函数
criterion=paddle.nn.MSELoss()
#3.2 优化器
optimizer=paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
# 4.开始迭代
epochs=500
final_checkpoint={}
for epoch in range(1,epochs+1):#前向传播#unsqueeze()扩展一维y_prd=model(x_train.unsqueeze(1))loss=criterion(y_prd.squeeze(1),y_train)#清除之前计算的梯度optimizer.clear_grad()#自动计算梯度loss.backward()#更新参数optimizer.step()# 5.显示频率的设置if epoch % 10==0 or epoch==1:#可以使用float(loss)或者 loss.numpy()会报警告print(f"epoch:{epoch},loss:{float(loss)}")#添加检查点程序if epoch==epochs:#把迭代次数写入final_checkpoint['epoch']=epoch#把训练损失写入final_checkpoint['loss']=loss#基础API模型的保存
paddle.save(model.state_dict(),'./基础API/model.pdparams')
#保存检查点checkpoint信息 是序列化的文件
paddle.save(final_checkpoint, "./基础API/final_checkpoint.pkl")

1.3.2 高级API模型的保存

1.3.2.1 训练fit进行保存

model.fit(dataloader,epochs=500,verbose=1,save_dir='./高层API1',save_freq=10)

#1.先来看数据加载
#2.模型构建高层API#导入库
import numpy as np
import paddle
import paddle.nn as nn
from paddle.io import DataLoader,TensorDataset
#设置随机数种子 ,保证结果可复现
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
#TensorDataset是接收一个值，不是接收两个值,使用列表
dataset=TensorDataset([x_train.unsqueeze(1),y_train.unsqueeze(1)])
#创建Dataloader对象
dataloader=DataLoader(dataset,batch_size=10,shuffle=True)
# 2. 定义前向模型
#方式2 单独定义 使用类的方式 class nn.Layer组网
class LinearModel(nn.Layer):def __init__(self):super(LinearModel,self).__init__()self.linear=nn.Linear(1,1)def forward(self,x):x=self.linear(x)return x
#定义模型的对象
model=LinearModel()# 3.使用高层api进行封装
# step1 使用paddle.Model(xxx)进行封装
model=paddle.Model(model)
#step2 使用prepare
model.prepare(optimizer=paddle.optimizer.SGD(learning_rate=0.01,parameters=model.parameters()),loss=nn.MSELoss(),metrics=paddle.metric.Accuracy())
#step3启动训练
#需要用到数据，训练轮次 是否显示日志过程
# model.fit(dataloader,epochs=500,verbose=1)#高级API模型的保存
#保存第一种方式,训练fit进行保存
model.fit(dataloader,epochs=500,verbose=1,save_dir='./高层API1',save_freq=10)

1.3.2.2 利用paddle.Model类进行保存

注意这边的model.save和基础API中的model.save不一样，基础API是自己申请出来的对象

# 这里是paddle.Model 大类

model.save('./高层API2/model') #save for train 动态图

# 静态图(可以c++调用)

model.save('./高层API2/infer_model',False) #save for inference 静态图(可以c++调用)

#1.先来看数据加载
#2.模型构建高层API#导入库
import numpy as np
import paddle
import paddle.nn as nn
from paddle.io import DataLoader,TensorDataset
#设置随机数种子 ,保证结果可复现
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
#TensorDataset是接收一个值，不是接收两个值,使用列表
dataset=TensorDataset([x_train.unsqueeze(1),y_train.unsqueeze(1)])
#创建Dataloader对象
dataloader=DataLoader(dataset,batch_size=10,shuffle=True)
# 2. 定义前向模型
#方式2 单独定义 使用类的方式 class nn.Layer组网
class LinearModel(nn.Layer):def __init__(self):super(LinearModel,self).__init__()self.linear=nn.Linear(1,1)def forward(self,x):x=self.linear(x)return x
#定义模型的对象
model=LinearModel()# 3.使用高层api进行封装
# step1 使用paddle.Model(xxx)进行封装
model=paddle.Model(model)
#step2 使用prepare
model.prepare(optimizer=paddle.optimizer.SGD(learning_rate=0.01,parameters=model.parameters()),loss=nn.MSELoss(),metrics=paddle.metric.Accuracy())
#step3启动训练
#需要用到数据，训练轮次 是否显示日志过程
# model.fit(dataloader,epochs=500,verbose=1)#高级API模型的保存
#保存第一种方式,训练fit进行保存
model.fit(dataloader,epochs=500,verbose=1)#保存方式2 利用paddle.Model类进行保存
#注意 这边的model.save和基础API中的model.save不一样，基础API是自己申请出来的对象
# 这里是paddle.Model 大类
model.save('./hig_API2/model') #save for train 动态图
# 静态图(可以c++调用)
model.save('./hig_API2/infer_model',False) #save for inference 静态图(可以c++调用)

1.4 paddlepaddle模型的加载

1.4.1 基础API模型的加载

model_state_dict=paddle.load('./基础API/model.pdparams')

模型和参数联系起来

model.set_state_dict(model_state_dict)

#导入库
import numpy as np
import paddle
import paddle.nn as nn
#设置随机数种子 ,保证结果可复现
from paddle.io import DataLoader,TensorDataset
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
# 2. 定义前向模型
# model=paddle.nn.Linear(1,1)#主要针对基础API
#方式1 使用序列的方式 nn.Sequential 组网
# model=nn.Sequential(nn.Linear(1,1))#方式2 单独定义 使用类的方式 class nn.Layer组网
class LinearModel(nn.Layer):def __init__(self):super(LinearModel,self).__init__()self.linear=nn.Linear(1,1)def forward(self,x):x=self.linear(x)return x
#定义模型的对象
model=LinearModel()# 3.定义损失函数和优化器
#3.1损失函数
criterion=paddle.nn.MSELoss()
#3.2 优化器
optimizer=paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
#基础API模型的加载
model_state_dict=paddle.load('./基础API/model.pdparams')
# optimizer_state_dict=paddle.load('./基础API/optimizer.pdopt')
# final_checkpoint_state_dict=paddle.load('./基础API/final_checkpoint.pkl')
# print(final_checkpoint_state_dict)#模型和参数联系起来
model.set_state_dict(model_state_dict)#训练 评估 和推理
# 模型验证模式
model.eval()
#使用TensorDateset 和DateLoader封装
dataloader_test=DataLoader(TensorDataset([paddle.to_tensor([1.5],dtype=paddle.float32)]),batch_size=1)#迭代
for x_test in dataloader_test:predict=model(x_test[0])print(predict)

1.4.2 高级API加载

import paddle
# 3.使用高层api进行封装
# step1 使用paddle.Model(xxx)进行封装
model=paddle.Model(model)
#高级API模型的加载
model.load("./高层API1/final")

#1.先来看数据加载
#2.模型构建高层API#导入库
import numpy as np
import paddle
import paddle.nn as nn
from paddle.io import DataLoader,TensorDataset
#设置随机数种子 ,保证结果可复现
seed=1
paddle.seed(seed)# 1.散点输入 定义输入数据
data = [[-0.5, 7.7], [1.8, 98.5], [0.9, 57.8], [0.4, 39.2], [-1.4, -15.7], [-1.4, -37.3], [-1.8, -49.1], [1.5, 75.6], [0.4, 34.0], [0.8, 62.3]]
#转化为数组
data=np.array(data)
# 提取x 和y
x_data=data[:,0]
y_data=data[:,1]
#转成张量 转成paddlepaddle张量
x_train=paddle.to_tensor(x_data,dtype=paddle.float32)
y_train=paddle.to_tensor(y_data,dtype=paddle.float32)
#TensorDataset是接收一个值，不是接收两个值,使用列表
dataset=TensorDataset([x_train.unsqueeze(1),y_train.unsqueeze(1)])
#创建Dataloader对象
dataloader=DataLoader(dataset,batch_size=10,shuffle=True)
# 2. 定义前向模型
#方式2 单独定义 使用类的方式 class nn.Layer组网
class LinearModel(nn.Layer):def __init__(self):super(LinearModel,self).__init__()self.linear=nn.Linear(1,1)def forward(self,x):x=self.linear(x)return x
#定义模型的对象
model=LinearModel()# 3.使用高层api进行封装
# step1 使用paddle.Model(xxx)进行封装
model=paddle.Model(model)
#step2 使用prepare
model.prepare(optimizer=paddle.optimizer.SGD(learning_rate=0.01,parameters=model.parameters()),loss=nn.MSELoss(),metrics=paddle.metric.Accuracy())#高级API模型的加载
model.load("./高层API1/final")
#验证
dataset=TensorDataset([paddle.to_tensor([1.5],dtype=paddle.float32),paddle.to_tensor([82],dtype=paddle.float32)])
datalaoder_eval=DataLoader(dataset)
eval_pre=model.evaluate(datalaoder_eval,verbose=1)
print(eval_pre)#预测
dataset=TensorDataset([paddle.to_tensor([1.5],dtype=paddle.float32)])
datalaoder_eval=DataLoader(dataset)
pre_result=model.predict(datalaoder_eval,verbose=1)
print(pre_result)

1.5 paddlepaddle模型网络结构的查看

1.5.1 summary

paddle.summary(model,(1,))

1.5.2 netron

netron pycharm 终端下输入 pip install netron

下载好后，在终端下输入 netron，在浏览器上输入 http://localhost:8080 即可

1.5.3 visualdl

安装网络查看库pip install visualdl==2.5.3

看文档查看结构网络(切记运行的程序不能有中文路径)

https://www.paddlepaddle.org.cn/documentation/docs/zh/guides/advanced/visualdl_usage_cn.html

这是使用visualdl写入

from visualdl import LogWriter

logwriter=LogWriter(logdir='logs')

这是使用visualdl查看

查看方式需要写上host 和port 不然不成功

visualdl --logdir ./logs --model ./logs/model.pdmodel --host 0.0.0.0 --port 8040

二、曲线拟合

从以下2个方面对曲线拟合进行介绍

1.曲线拟合算法理论讲解

2.编程实例与步骤

上面这2方面的内容，让大家，掌握并理解曲线拟合算法。

1.1案例引入

蝌蚪变青蛙

在某池塘中，有某类蝌蚪，它们随着天数的增加，开始慢慢需要觅食，在需要觅食之前，都是从卵黄带来的营养维持生命。

于是采集了7只蝌蚪是否需要觅食的数据：

横坐标的单位是天数；

纵坐标是否需要觅食，0是不需要觅食，1是需要觅食。

如右图所示 x轴表示天数，y轴表示是否需要觅食。

1.2 散点输入

本实验中，采集了天数与是否觅食的的关系数据，x轴表示天数，y轴表示是否觅食，0表示不需要觅食，1表示需要觅食，从图上看有3只蝌蚪是不需要觅食的，3天以下的不需要觅食。有4只需要觅食，大于3天的需要觅食。

并且将它们绘制在一个二维坐标中，其分布如下图所示：

坐标分别为[0.8, 0]，[1.1, 0] ，[1.7, 0] ，[3.2, 1] ，[3.7, 1] ，[4.0, 1] ，[4.2, 1]。

1.3 前向计算

我们的目的是拟合这些散点，通过前向计算，我们通过修改w和b只能部分点落在线上，从实验看直线无法拟合这些点。

直线无法拟合那应该怎么办呢？

对于直线无法拟合这些点，是不是需要将直线变成曲线来拟合这些散点，在没有引入直线变曲线之前，使用直线是无法拟合这些点的。

这个σ是一个激活函数。

如果σ是阶跃函数，

那么这个阶跃函数的缺点是什么？

不连续性：在x=2.5处不连续；

不可导性：在x=2.5处不存在导数；

怎么解决阶跃函数导数不存在的问题呢？

是不是得找一个函数它要处处可微，是连续的，在各个地方都可导的，是不是就能很好的拟合当前曲线了。

1.4 Sigmoid函数引入

sigmoid拟合数据点效果图

下面引入Sigmoid函数，当然是是前人慢慢发现的这个函数

Sigmoid的函数，其函数公式为：

其函数图像如下所示：

的值域处于（0，1）之间，两边无限接近于0和1。但永远不等于0和1。定义域是负无穷到正无穷。

在线性回归中，直线的方程是

，带入Sigmoid激活函数中，得到：

1.5 激活函数的引入

在该实验中，将直线转换成曲线，可以在直线

加入一个新的函数

，这个是一个激活函数，在上面实验中使用的激活函数是Sigmoid函数，当然还有其他激活函数，后面的课程会讲。

激活函数是神经网络中一种重要的非线性函数，其作用在于引入非线性特性，使得神经网络能够学习和表示更加复杂的数据模式和关系。激活函数通常在每个神经元的输出上应用，将输入信号转换为输出信号。

以下是激活函数的主要作用：

引入非线性特性：如果在神经网络中只使用线性变换，例如线性加权和求和，那么整个网络的组合效果将仍然是线性的。激活函数的非线性特性能够在每个神经元上引入非线性转换，从而让神经网络能够学习和表示更加复杂的函数和数据模式。
提高模型的表达能力：激活函数的引入增加了神经网络的表达能力，使得网络可以逼近任何复杂的函数，这种特性称为“普遍逼近定理”（Universal Approximation Theorem）。
稀疏性和稳定性：一些激活函数(如Relu)具有稀疏性和稳定性的特点，可以缓解梯度消失和梯度爆炸的问题，从而有助于训练更深的神经网络。

梯度消失简单解释：w新=w旧-学习率*梯度 (梯度为0 w新一直等于w旧，引起w不更新就是梯度消失)

梯度爆炸简单解释：w新=w旧-学习率*梯度 (梯度非常大，只要大于1，因为模型会有很多层，链式求导法则需要连乘，就会导致梯度爆炸。)

综上所述，激活函数在神经网络中扮演着非常重要的角色，它们的引入使得神经网络具备非线性表达能力，从而能够处理和解决更加复杂的任务。

1.6 参数初始化

在之前的前向计算中，可以通过改变自己修改w和b来拟合这条曲线，但是在很多实际场景中，并没办法做到直接求出最优的w，b值，所以需要先随机定一个w和b，然后让梯度下降去拟合这些点。

在“参数初始化”组件中，可以初始化w和b的值以及学习率的值。

1.7 损失函数

根据公式：

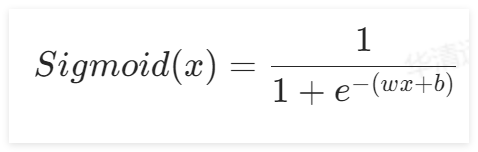
入均方差损失函数中，于是损失函数就成了：

1.8 开始迭代

定义好损失函数后，选择好迭代次数，然后就可以进行反向传播了。

1.9反向传播

在上面得到了损失函数的表达式，本实验中使用梯度下降的方式去降低损失函数值，于是需要对损失函数进行求导：

将其拆分成复合函数，得到：

对复合函数求导，可得：

该过程对应了本实验中的“反向传播”组件，其内容如下所示：

1.10 梯度下降显示

为了更好的观察到迭代过程中的参数变化和损失函数的变化，提供了“显示频率组件”，其内容如下图所示：

通过设置显示频率，可以实时反馈当前的参数值和损失值，在“梯度下降显示”组件中可以查看，其组件内容如下图所示：

在该图像中，1.46对应的是w的值，-3.27对应的是b的值，0.03是损失值，这三个值都是根据显示频率实时反馈回来的。

左边的图像是根据当前的w和b的值所绘制的曲线，右边的图像是绘制的损失值的变化。

1.11 曲线拟合代码

import numpy as np  # 导入 numpy 库，用于数值计算
import matplotlib.pyplot as plt  # 导入 matplotlib.pyplot 库，用于绘图# 原始数据，第一列是 x，第二列是 y（标签）
data = np.array([[0.8, 0], [1.1, 0], [1.7, 0], [3.2, 1], [3.7, 1], [4.0, 1], [4.2, 1]])data = np.array(data)  # 转换为 numpy 数组 (虽然这里重复了，但保留了原始代码)x_data = data[:, 0]  # 获取所有行的第一列 (x 值)
y_data = data[:, 1]  # 获取所有行的第二列 (y 值，也就是标签)# 定义 sigmoid 函数
def sigmoid(x):return 1 / (1 + np.exp(-x))  # sigmoid 函数的公式w = 0  # 初始化权重 w
b = 0  # 初始化偏置 b
l = 0.05  # 学习率 learning rate
epochs = 1000  # 迭代次数
fig, (ax1, ax2) = plt.subplots(2, 1)  # 创建一个包含两个子图的 figure，垂直排列
epoch_list = []  # 用于存储 epoch 的列表，用于绘制损失曲线
loss_list = []  # 用于存储 loss 的列表，用于绘制损失曲线# 迭代训练
for i in range(1, epochs + 1):z = w * x_data + b  # 计算线性模型的输出a = sigmoid(z)  # 将线性输出通过 sigmoid 函数，得到预测值loss = np.mean((y_data - a) ** 2)  # 计算均方误差损失epoch_list.append(i)  # 将当前 epoch 添加到 epoch_listloss_list.append(loss)  # 将当前 loss 添加到 loss_list# 反向传播，计算梯度deda = -2 * (y_data - a)  # loss 对 a 的导数dadz = a * (1 - a)  # sigmoid 函数的导数dzdw = x_data  # z 对 w 的导数dzdb = 1  # z 对 b 的导数dw = np.mean(deda * dadz * dzdw)  # 计算 w 的梯度db = np.mean(deda * dadz * dzdb)  # 计算 b 的梯度# 更新权重和偏置w = w - l * dw  # 更新 wb = b - l * db  # 更新 b# 每 50 个 epoch 或第一个 epoch，打印 loss 并更新图表if i % 50 == 0 or i == 1:print(f"epoch:{i},loss:{loss}")  # 打印 epoch 和 loss# 画图显示x_min = x_data.min()  # x 最小值x_max = x_data.max()  # x 最大值# 按照等间隔从x_min到x_max之间的数据x_values = np.linspace(x_min, x_max, int(x_max - x_min) * 10)  # 在 x_min 和 x_max 之间创建一系列均匀间隔的值y_values = sigmoid(w * x_values + b)  # 计算 sigmoid 函数的值# 画第一个图ax1.clear()  # 清除 ax1ax1.scatter(x_data, y_data, color='b')  # 画散点图# 画曲线ax1.plot(x_values, y_values, c='r')  # 画 sigmoid 曲线ax1.set_title(f"Curve Regression: w={round(w, 3)}, b={round(b, 3)}")  # 设置 ax1 的标题# 画 ax2ax2.clear()  # 清除 ax2ax2.plot(epoch_list, loss_list, color='g')  # 画损失曲线ax2.set_xlabel("Epoch")  # 设置 x 轴标签ax2.set_ylabel("Loss")  # 设置 y 轴标签ax2.set_title(f"Loss Curve")  # 设置 ax2 的标题plt.pause(1)  # 暂停 1 秒，以便显示图表

三、激活函数

从以下3个方面对激活函数及其导数进行介绍
1.激活函数及其导数算法理论讲解
2.编程实例与步骤
3.实验现象
上面这3方面的内容，让大家，掌握并理解激活函数及其导数算法。

3.1 激活函数及其导数算法理论讲解

24年刚出版的<<激活函数的三十年：神经网络 400 个激活函数的综合调查>>

《Three Decades of Activations: A Comprehensive Survey of 400 Activation Functions for Neural Networks》

包括常用的激活函数和不常用的，400种，大家如果感兴趣可以看看。

文件分享https://share.weiyun.com/3t76DytU

3.2 激活函数的作用？

激活函数的作用就是在神经网络中经过线性计算后，进行的非线性化。

下面讲解Sigmoid，tanh、Relu，Leaky Relu、Prelu、Softmax、ELU七种激活函数。

3.3 激活函数的概念

激活函数给神经元引入了非线性因素，让神经网络可以任意逼近任何非线性函数，

通俗理解为把线性函数转换为非线性函数

3.4 Sigmoid

Sigmoid的函数公式为：

函数图像如下图所示：

该函数处于（0，1）之间，两边无限接近于0和1，但永远不等于0和1。

sigmoid函数的导数公式为：

导数图像为：

Sigmoid特点总结：

Sigmoid 函数的输出范围被限制在 0 到 1 之间，这使得它适用于需要将输出解释为概率或者介于 0 和 1 之间的任何其他值的场景。
Sigmoid 函数的两端，导数的值非常接近于零，这会导致在反向传播过程中梯度消失的问题，特别是在深层神经网络中。

Sigmoid激活函数有着如下几种缺点：

梯度消失：Sigmoid函数趋近0和1的时候变化率会变得平坦，从导数图像可以看出，当x值趋向两侧时，其导数趋近于0，在反向传播时，使得神经网络在更新参数时几乎无法学习到低层的(不明显的)特征，从而导致训练变得困难。 w新=w旧-lr*梯度

不以零为中心：Sigmoid函数的输出范围是0到1之间，它的输出不是以零为中心的，会导致其参数只能同时向同一个方向更新，当有两个参数需要朝相反的方向更新时，该激活函数会使模型的收敛速度大大的降低

计算成本高：Sigmoid激活函数引入了exp()函数，导致其计算成本相对较高，尤其在大规模的深度神经网络中，可能会导致训练速度变慢。

不是稀疏激活：Sigmoid函数的输出范围是连续的，并且不会将输入变为稀疏的激活状态。在某些情况下，稀疏激活可以提高模型的泛化能力和学习效率。

不以零中心有什么问题？举例讲解：

此时，模型为了收敛，w0、w1…改变的方向是统一的，或正或负。所以如果你的最优值是需要w0增加，w1减少，那么不得不向逆风前行的风助力帆船一样，走 Z 字形逼近最优解。如下图所示

模型参数走绿色箭头能够最快收敛，但由于输入值的符号总是为正，所以模型参数可能走类似红色折线的箭头。如此一来，使用 Sigmoid 函数作为激活函数的神经网络，收敛速度就会慢上不少了。

总结

本文详细介绍了PaddlePaddle框架下线性回归的实现，从模型定义到加载，再到网络结构查看，提供了全面的指导。同时，文章还讲解了曲线拟合的原理，并重点介绍了Sigmoid等激活函数及其导数，强调了激活函数在神经网络中的重要作用。通过本文的学习，读者可以不仅掌握PaddlePaddle的基本使用，还能深入理解线性回归、曲线拟合以及激活函数等核心概念，为后续的深度学习研究打下坚实的基础。