2194出差-节点开销Bellman-ford/图论
题目网址: 蓝桥账户中心

我先用Floyd跑了一遍,不出所料TLE了
n,m=map(int,input().split())c=list(map(int,input().split()))INF=float('inf')
ma=[[INF]*n for i in range(n)]for i in range(m):u,v,w=map(int,input().split())ma[u-1][v-1]=wma[v-1][u-1]=w#“道路”:双向for k in range(n):for i in range(n):for j in range(n):ma[i][j]=min(ma[i][j],ma[i][k]+ma[k][j]+c[k])print(ma[0][n-1])
边集数组
n,m=map(int,input().split())#节点cost,注意:起点和终点得设为0. ------------
c=list(map(int,input().split()))c[0]=0
c[n-1]=0
#------------------------------------------edges=[]for i in range(m):u,v,w=map(int,input().split())edges.append((u,v,w))#别忘记双向边edges.append((v,u,w))注意:起点和终点的cost得清洗为0(后面会具体解释)
而且本题是双向边,得两次edges.append( )
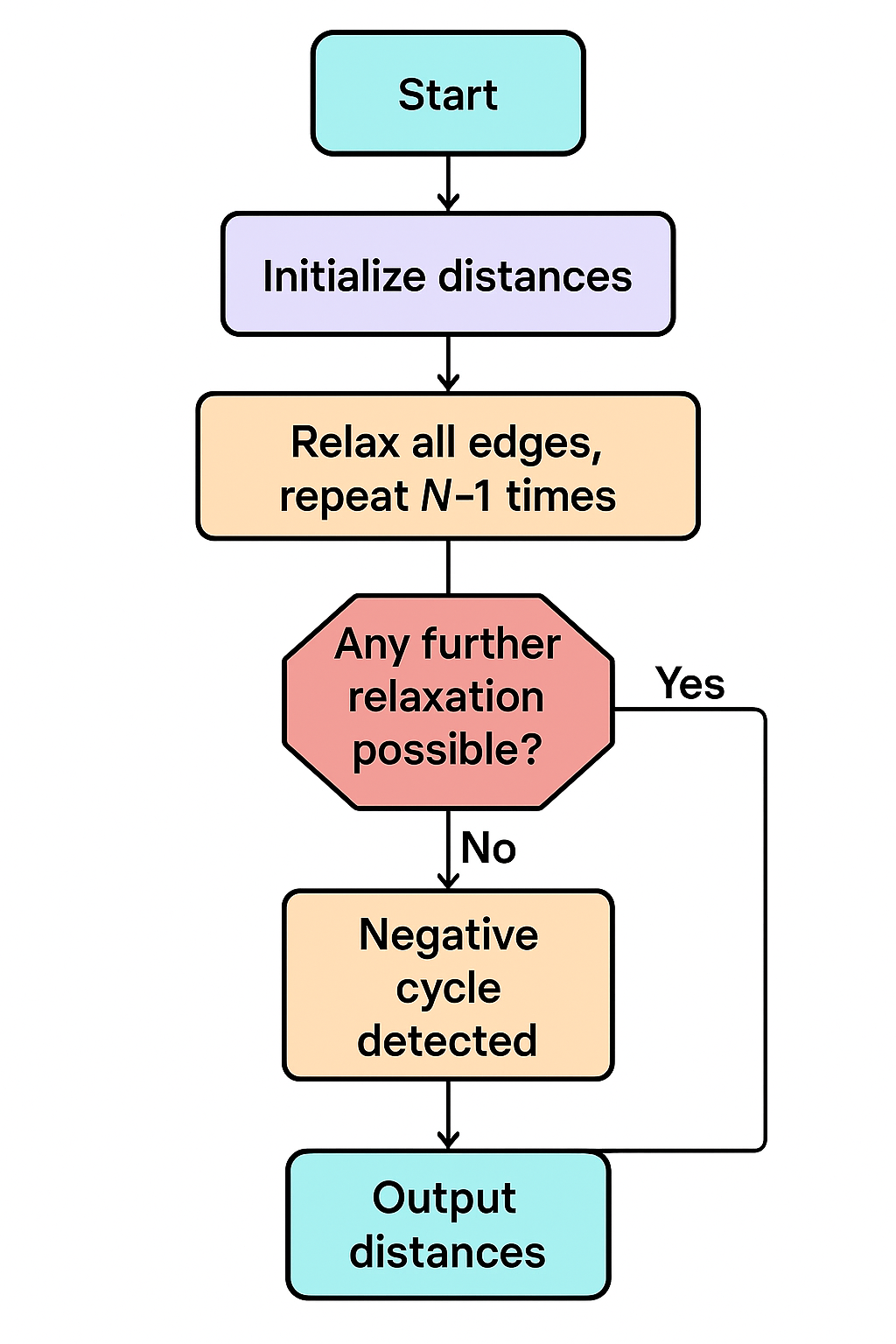
Bellman-ford算法
从起点向外传递最短路信息,得经过n-1次松弛才能到达终点
前(n-1)轮检视所有的边(u,v,c),进行松弛操作(判断所有边能否使新路径更小):
(如果第n轮还有更小的那就是存在负环了)
sta去v的新路径:从sta先去u城,加上从u城到v的代价c ,还得加上城市点的cost
但是是u城的cost还是v城的cost?
d[ k ]代表从sta到k点的最小花费,为了方便统计我们得讲所有在路径上的点的话费都算在里面,这也就是为什么前面需要清洗起点和终点的cost为0
那么新路径应该加上的不是中介点u的cost,而是新的v的,这点和floyd的点花费处理不同
(floyd是多源最短路,而bellman是单源最短路)
def bellman(n,edges,sta,c):INF=float('inf')d=[INF]*(n+1) #注意输入起始从1开始,所以得n+1 ,初始化无边d[sta]=0 #d数组是从sta到各点的最短路径,自己到自己为0#n-1轮松弛for i in range(n-1):for u,v,w in edges:if d[u]!=INF:ncost=d[u]+w+c[v-1]#注意c的索引if ncost<d[v]:#从sta有边到u ,而且新路径更短d[v]=ncost#第n轮:检测负环for u,v,w in edges:if d[u]!=INF and d[u]+w+c[v-1]<d[v]:return Nonereturn dd=bellman(n,edges,1,c) #注意起始从1开始
if d:print(d[n]) #从点1到点n
else:print('有负环')