堆和二叉树的概念和操作

目录

1.树的概念

 1.1数的表示

1.2二叉树

 1.3特殊的二叉树

1.3.1满二叉树

 1.3.2完全二叉树

1.3.3 二叉树存储结构

 2.堆

2.1堆的实现

初始化和销毁

 堆的插入

 堆的向上调整算法​编辑

​编辑

 堆的删除

 出堆顶

---

1.树的概念

树是非线性的数据结构，有限节点具有的层次关系的集合。

根节点：有且只有一个根节点，没有前驱。其余节点被分成互不相交的树

除根节点外每个节点都有一个前驱节点。

⼀棵N个结点的树有N-1条边

 ⽗结点/双亲结点：若⼀个结点含有⼦结点，则这个结点称为其⼦结点的⽗结点； 如上图：A是B的父结点

⼦结点/孩⼦结点：⼀个结点含有的⼦树的根结点称为该结点的⼦结点； 如上图：B是A的孩⼦结点

结点的度：⼀个结点有⼏个孩⼦，他的度就是多少；⽐如A的度为6，F的度为2，K的度为0

树的度：⼀棵树中，最⼤的结点的度称为树的度； 如上图：树的度为 6

叶⼦结点/终端结点：度为 0 的结点称为叶结点； 如上图： B、C、H、I... 等结点为叶结点

分⽀结点/⾮终端结点：度不为 0 的结点； 如上图： D、E、F、G... 等结点为分⽀结点（非叶子节点）

兄弟结点：具有相同⽗结点的结点互称为兄弟结点(亲兄弟)； 如上图： B、C 是兄弟结点

结点的层次：从根开始定义起，根为第 1 层，根的⼦结点为第 2 层，以此类推；

树的⾼度或深度：树中结点的最⼤层次； 如上图：树的⾼度为 4

结点的祖先：从根到该结点所经分⽀上的所有结点；如上图： A 是所有结点的祖先

路径：⼀条从树中任意节点出发，沿⽗节点-⼦节点连接，达到任意节点的序列；⽐如A到Q的路径为： A-E-J-Q；H到Q的路径H-D-A-E-J-Q

⼦孙：以某结点为根的⼦树中任⼀结点都称为该结点的⼦孙。如上图：所有结点都是A的⼦孙

森林：由 m（m>0） 棵互不相交的树的集合称为森林；

 1.1数的表示

孩子兄弟表示法

struct TreeNode 
{
Struct Node * child; //第一个孩子节点struct Node  * brother ;//孩子的兄弟节点int  data;//数据域
}

1.2二叉树

二叉树是树形结构的一种。最常⽤的就是⼆叉树，⼀棵⼆叉树是结点的⼀个有限集合，该集合由⼀个根结点 加上两棵别称为左⼦树和右⼦树的⼆叉树组成或者为空。

1. ⼆叉树不存在度⼤于 2 的结点

2. ⼆叉树的⼦树有左右之分，次序不能颠倒，因此⼆叉树是有序树

注意：对于任意的⼆叉树都是由以下⼏种情况复合⽽成的

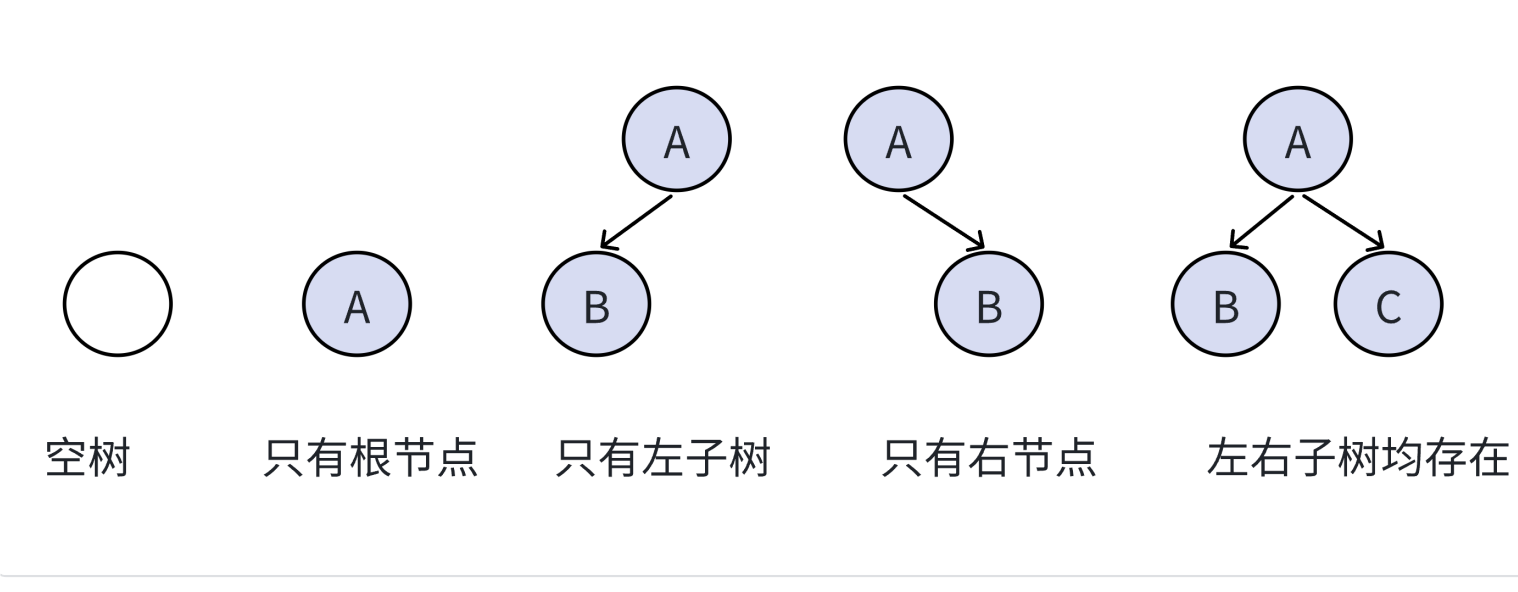
 1.3特殊的二叉树

1.3.1满二叉树

每⼀个层的结点数都达到最⼤值，则这个⼆叉树就是满⼆叉树。如果⼀ 个⼆叉树的层数为 K

且节点总数为2的k次方-1，这个就是满二叉树。

 1.3.2完全二叉树

完全⼆叉树是由满⼆叉树⽽引出来的。对于深度为 K 的，有 n 个 结点的⼆叉树，当且仅当其每⼀个结点都与深度为K的满⼆叉树中编号从 1 ⾄ n 的结点⼀⼀对应时称 之为完全⼆叉树。要注意的是满⼆叉树是⼀种特殊的完全⼆叉树。

除了第k层  每层节点的个数都达到最大个数 ，第k层的个数不一定是最大节点个数

 完全二叉树的结点的顺序是从左到右的。

完全二叉树是满二叉树的一种 ，完全二叉树不一定是满二叉树，满二叉树一定是完全二叉树

根据满⼆叉树的特点可知：

1）若规定根结点的层数为 1 ，则⼀棵⾮空⼆叉树的第i层上最多有 2 的i−1 次方个结点

2）若规定根结点的层数为 1 ，则深度为 h 的⼆叉树的最⼤结点数是 2 的h次方 -1 比特就业课

3）若规定根结点的层数为 1 ，具有 n 个结点的满⼆叉树的深度 h= log 2 (n+1) ( log 以2为底， n+1 为对数)

1.3.3 二叉树存储结构

二叉树有两种存储机构 ：顺序结构 、链式结构。

顺序结构

顺序结构存储就是使⽤数组来存储，⼀般使⽤数组只适合表⽰完全⼆叉树，因为不是完全⼆叉树会有空间的浪费，完全⼆叉树更适合使⽤顺序结构存储。

通常把堆（⼀种⼆叉树）使⽤顺序结构的数组来存储，需要注意的是这⾥的堆和操作系统 虚拟进程地址空间中的堆是两回事，⼀个是数据结构，⼀个是操作系统中管理内存的⼀块区域分段

链式存储

 链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别⽤来给出该结点左孩⼦和右孩 ⼦所在的链结点的存储地址

 2.堆

堆分为大根堆和小跟堆

堆也是一种特殊的二叉树，⼀般堆使⽤顺序结构的数组来存储数据。

 上面可以得出 小根堆的父节点比子节点要小，大根堆的父节点比子节点要大。

堆总是完全二叉树

二叉树性质

对于具有 n 个结点的完全⼆叉树，如果按照从上⾄下从左⾄右的数组顺序对所有结点从 0 开始编号，则对于序号为 i 的结点有：

用下标来进行

1. 若 i>0 ， i 位置结点的双亲序号： (i-1)/2 ； i=0 ， i   为根结点编号，⽆双亲结点   子节点求出 父节点

2. 若 2i+1=n 否则⽆左孩⼦ 

3. 若 2i+2=n 否则⽆右孩

2.1堆的实现

初始化和销毁

 

 

 堆的插入

大家可以来实现一下 这个很类似于单链表的插入

 堆的向上调整算法

 经过调试后可以看出是小根堆

 小根堆的展示方法

 

 堆的删除

先交换首尾结点 ，后删除尾结点，堆顶向下调整 直至child >n

 下面我们可以把数组里的数据拆解一下

 出堆顶

 可以将下面的堆进行排序

 

 结果是没问题的 得出的是小根堆

 这节课就告一段落了，下个章节见

Heap.c

#define _CRT_SECURE_NO_WARNINGS
#include "Heap.h"
//初始化
void HPInit(HP* php)
{assert(php);php->arr = NULL;php->capacity = php->size = 0;}
//销毁
void HPDestory(HP* php)
{assert(php);if (php->arr){free(php->arr);}php->arr = NULL;php->capacity = php->size = 0;}
//交换数据
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;}
//向上调整算法
void AdjustUp(HPDatatyp* arr, int child)
{int  parent = (child - 1) / 2;while (child > 0)//当child为0的时候 说明走到了根节点{if (arr[child] < arr[parent]){Swap(&arr[parent], &arr[child]);child = parent;parent = (child - 1) / 2;}else{break;}}}void  HPPush(HP* php,HPDatatyp x)
{assert(php);//判断空间是否足够if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDatatyp* tmp = (HPDatatyp*)realloc(php->arr, newcapacity * sizeof(HPDatatyp));if (tmp == NULL){perror("realloc fail");exit(1);}php->arr = tmp;php->capacity = newcapacity;}php->arr[php->size] = x;AdjustUp(php->arr , php->size );++php->size;
}//向下调整
void  AdjustDown(HPDatatyp* arr, int parent, int n)
{int child = parent * 2 + 1;//左右孩子中找最小的孩子 和父结点比较while (child <n){if (child +1  <n && arr[child] > arr[child + 1]){child++;}if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);//这里记得要传地址parent = child ;child = parent * 2 + 1;}//如果child大于parent 那么就跳出else{break;}}}
void HPPop(HP* php)
{assert(php && php->size);Swap(&php->arr[0], &php->arr[php->size - 1]);//第一步交换首尾结点--php->size;AdjustDown(php->arr, 0, php->size); //向下调整}
bool HPEmpty(HP* php)//堆为空
{assert(php);return  php->size == 0;}HPDatatyp  HPTop(HP* php) // 出堆顶
{assert(php && php->size);return php->arr[0];}

 Heap.h

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
typedef int HPDatatyp;typedef struct Heap
{HPDatatyp* arr; int size;//个数int capacity; //容量}HP;void HPInit(HP* php);void HPDestory(HP* php);//插入数据void  HPPush(HP* php,HPDatatyp x);//删除数据void HPPop(HP* php);//出堆顶HPDatatyp   HPTop(HP* php);//堆空bool HPEmpty(HP* php);

text,c

#define _CRT_SECURE_NO_WARNINGS
#include "Heap.h"
void HPtext()
{HP  hp;HPInit(&hp);int arr[] = { 12,34,56,32,43,25,45 };for (int  i = 0; i <= 6; i++){HPPush(&hp, arr[i]); }//HPPop(&hp);while (!HPEmpty(&hp)){printf("%d ", HPTop(&hp));HPPop(&hp);}HPDestory(&hp);}
int main()
{HPtext();return 0;
}