Scratch——第20课 辗转相除法/绳子算法

辗转相除法是用于求取最大公约数时需要用到的方法，它还有个名字称为绳子算法，这类题目只要理解辗转相处的原理即可拿下。

一、辗转相除法的基本原理

两个整数的最大公约数不变，当较大数减去较小数后，得到的差值与较小数的最大公约数相同。以下是算法的步骤：

1.设两个正整数 a 和 b ，且 a > b 。

2.用 a 除以 b ，得到余数 r (0 < r < b) 。

3.如果 r 为 0 ，则 b 即为两数的最大公约数。

4.如果 r ≠ 0 ，则令 a = b ， b = r ，并返回第二步。

这个过程将不断重复，每次都会产生一个更小的正整数，直到余数为 0 ，此时的 b 就是最大公约数。

二、往年题目

1.（CIE-202203）求最大公约数

1.准备工作

（1）保留默认白色背景和小猫角色。

2.功能实现

（1）输入两个正整数；

（2）小猫说出这两个数的最大公约数。

解题思路：

第①步：通过询问得到两个整数，运用询问和，第二次的回答将顶替掉第一次的回答，那么可以通过变量的设置，然后让回答存储到相对应的变量中。

第②步：判断a是否大于b，如果不满足，那么变量进行交换，在交换的过程中，需要一个中介的变量，要不然待会无法完成交换的操作（详细的原因可以看第13课的变量互换）

第③步：用 a 除以 b ，得到余数c (0 <c < b),将得到的余数进行判断，是否等于0，等于0，跳出循环，这时可以运用（这个命令是重复执行直到满足条件就跳出循环，不满足条件就继续循环的操作），那么条件就是

第④步： 若余数c不等于0，那么令 a = b ， b =c，并继续相除 

第⑤步：余数等于0停止循环，输出最大公约数。

整合代码：

2.（CIE-202104）绳子算法

故事情境：最近在学绳子算术的小星星非常苦恼，他常常在想，如果有一款程序能实现根据输入的两根绳子长度，可以把两根长绳截成长度相等的小段后，直接求出一共可以截成多少段，每段最长多少米就好了。小猫知道后，决定设计一个程序帮助小星星走出绳子算术的困境。

1.准备工作

(1)保留舞台默认白色背景及小猫角色，将小猫角色调整到舞台上合适的位置；

(2)建立名为“绳子”的列表用于存储数据。

2.功能实现

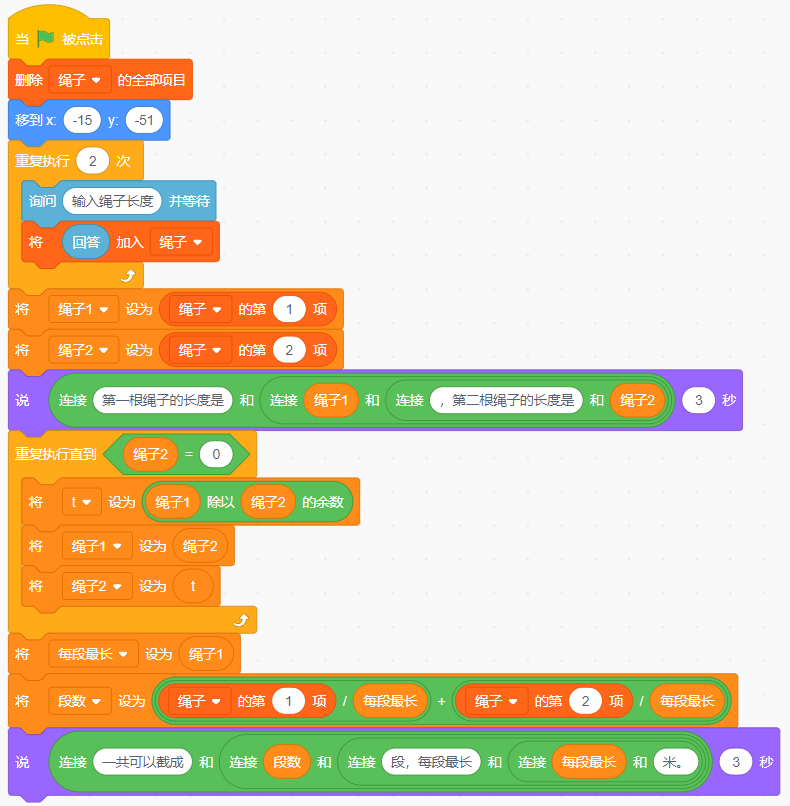
(1)点击绿旗，询问“输入绳子长度”并等待；

(2)将输入的绳子长度保存到列表“绳子”后，小猫分别说两根绳子的长度3秒；

(3)根据输入的两根绳子长度，设计算法实现：把两根长绳截成长度相等的小段。求出一共可以截成多少段，每段最长多少米；

(4)计算完成后，小猫分别说“一共可以截成多少段，每段最长多少米。”3秒。

解题思路：

第①步：询问“输入绳子长度”并等待，将得到的回答插入到列表中

第②步：将两条绳子的长度说出来，那么这时候，可以让其变量等于第一项和第二项，然后运用字符串拼接的方法，说出两根绳子的长度

第③步：用 绳子1除以绳子2，得到余数t (0 <t < b),将得到的余数进行判断，是否等于0，等于0，跳出循环，这时可以运用（这个命令是重复执行直到满足条件就跳出循环，不满足条件就继续循环的操作），那么条件就是

第④步： 若余数t不等于0，那么令绳子1=绳子2， 绳子2=t，并继续相除 

第⑤步：余数等于0停止循环，输出最大公约数​​​​​​​。

第⑥步：接着，计算段数，最后运用拼接字符串的方法说出每段最长和段数。

整合代码：