蚁群算法是一种模拟蚂蚁觅食行为的优化算法,适合用于解决旅行商问题(TSP)
蚁群算法是一种模拟蚂蚁觅食行为的优化算法,适合用于解决旅行商问题(TSP)。以下是使用 MATLAB 实现蚁群算法解决 50 个城市 TSP 问题的代码:
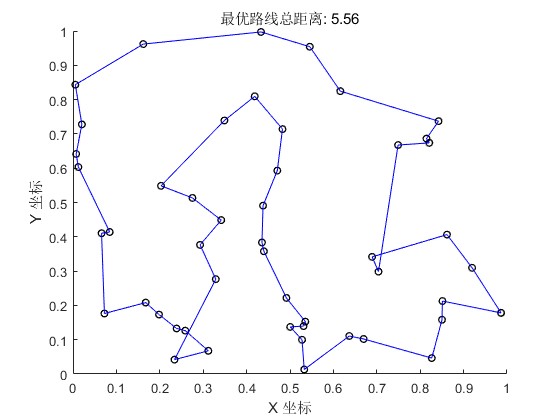
代码说明:
- 城市坐标生成:利用
rand(numCities, 2)随机生成 50 个城市的坐标,接着算出城市之间的距离矩阵。 - 蚁群算法参数设置:对蚂蚁数量、迭代次数、信息素重要程度因子、启发式因子、信息素挥发因子以及信息素增加强度系数等参数进行设置。
- 信息素矩阵初始化:把信息素矩阵初始化为全 1 矩阵。
- 蚁群算法主循环:
- 每只蚂蚁随机选择起始城市,再依据信息素和距离计算转移概率,采用轮盘赌的方式选择下一个城市,从而构建完整的路径。
- 计算每只蚂蚁路径的总距离,更新最优解。
- 按照信息素挥发和增加规则更新信息素矩阵。
- 绘制最优路线:将最优路线首尾相连,然后绘制出城市和最优路线。
运行这段代码后,你会看到 50 个城市的最优旅行路线以及对应的总距离。
% 随机生成 50 个城市的坐标
numCities = 50;
cities = rand(numCities, 2);% 计算城市之间的距离矩阵
distMatrix = pdist2(cities, cities);% 蚁群算法参数设置
numAnts = 50; % 蚂蚁数量
numIterations = 200; % 迭代次数
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发式因子
rho = 0.5; % 信息素挥发因子
Q = 100; % 信息素增加强度系数% 初始化信息素矩阵
pheromoneMatrix = ones(numCities, numCities);% 初始化最优解
bestRoute = [];
bestDistance = Inf;% 蚁群算法主循环
for iter = 1:numIterations% 初始化所有蚂蚁的路径allRoutes = zeros(numAnts, numCities);allDistances = zeros(numAnts, 1);% 每只蚂蚁构建路径for ant = 1:numAnts% 随机选择起始城市currentCity = randi(numCities);unvisitedCities = setdiff(1:numCities, currentCity);route = currentCity;% 依次选择下一个城市for i = 2:numCities% 计算转移概率probabilities = (pheromoneMatrix(currentCity, unvisitedCities).^alpha) .* ((1./distMatrix(currentCity, unvisitedCities)).^beta);probabilities = probabilities / sum(probabilities);% 轮盘赌选择下一个城市nextCityIndex = randsample(length(unvisitedCities), 1, true, probabilities);nextCity = unvisitedCities(nextCityIndex);% 更新路径和未访问城市集合route = [route nextCity];unvisitedCities = setdiff(unvisitedCities, nextCity);currentCity = nextCity;end% 记录当前蚂蚁的路径和总距离allRoutes(ant, :) = route;allDistances(ant) = calculateTotalDistance(route, distMatrix);end% 更新最优解[minDistance, minIndex] = min(allDistances);if minDistance < bestDistancebestDistance = minDistance;bestRoute = allRoutes(minIndex, :);end% 更新信息素矩阵pheromoneMatrix = (1 - rho) * pheromoneMatrix;for ant = 1:numAntsroute = allRoutes(ant, :);for i = 1:numCities - 1pheromoneMatrix(route(i), route(i + 1)) = pheromoneMatrix(route(i), route(i + 1)) + Q / allDistances(ant);pheromoneMatrix(route(i + 1), route(i)) = pheromoneMatrix(route(i + 1), route(i)) + Q / allDistances(ant);endpheromoneMatrix(route(numCities), route(1)) = pheromoneMatrix(route(numCities), route(1)) + Q / allDistances(ant);pheromoneMatrix(route(1), route(numCities)) = pheromoneMatrix(route(1), route(numCities)) + Q / allDistances(ant);end
end% 回到起始城市
bestRoute = [bestRoute bestRoute(1)];% 绘制最优路线
figure;
hold on;
plot(cities(:, 1), cities(:, 2), 'ko', 'MarkerSize', 5, 'LineWidth', 1); % 绘制城市
for j = 1:numCitiesstartCity = bestRoute(j);endCity = bestRoute(j + 1);plot([cities(startCity, 1) cities(endCity, 1)], [cities(startCity, 2) cities(endCity, 2)], 'b-', 'LineWidth', 0.5);
end
title(sprintf('最优路线总距离: %.2f', bestDistance));
xlabel('X 坐标');
ylabel('Y 坐标');
hold off;% 计算总距离的函数
function totalDistance = calculateTotalDistance(route, distMatrix)numCities = length(route);totalDistance = 0;for i = 1:numCities - 1totalDistance = totalDistance + distMatrix(route(i), route(i + 1));endtotalDistance = totalDistance + distMatrix(route(numCities), route(1)); % 回到起始城市
end 