城市群出行需求的时空分形

城市群出行需求的时空分形

原文：He, Zhengbing. “Spatial-temporal fractal of urban agglomeration travel demand.” Physica A: Statistical Mechanics and its Applications 549 (2020): 124503.

1. Introduction（引言）

• 城市区域的重要性：开篇指出城市区域（urban agglomeration）是城市高度发展的空间形式，在城市化、信息技术和交通快速发展的背景下，已成为全球经济和人类活动的重要载体。列举了全球一些典型的城市区域，如美国的南加州、五大湖地区，欧洲的蓝香蕉地带、金香蕉地带，中国的长江三角洲、京津冀，阿根廷的大布宜诺斯艾利斯，巴西的圣保罗大都市区等。
• 研究现状与不足：提到城市区域因在经济和人类活动中的重要性而受到广泛关注，相关研究数量在Web of Science上从2000年的5488篇激增到2015年的32231篇。其中不少研究从城市形态角度出发，探讨城市区域如何增长扩张及主要影响因素。此外，人类在城市内外的日常移动（人类流动性）也是重要研究方向，但以往研究大多聚焦于城市内部的人类流动性，对于城市区域尺度的人类流动性关注较少，而城市区域是介于城市和国家之间的重要尺度。
• 研究目的与方法：鉴于城市区域的不断发展以及现有研究的空白，文章旨在理解城市区域的旅行需求，因为旅行需求是驱动人类流动的基本因素之一。为此，文章首先对空间区域进行单元或区域分解，这是理解旅行需求的首要步骤。然而，以往研究在此过程中大多未深入讨论单元大小对结果的影响。基于此，本文以台湾地区为例（典型的城市区域），以出租车需求为研究对象（代表性的旅行需求），通过空间-时间分解构建城市区域旅行需求网络，分析其属性，特别是网络的度分布情况，以揭示城市区域旅行需求的本质和人类流动性规律。

2. Taiwan and Taxi Data in Taiwan（台湾及其出租车数据）

• 台湾概况：台湾是一个岛屿，面积35883平方公里，2016年人口23269633人。其主要城市包括台北、新北、台中、台南、高雄等，是一个典型的具有连续城市区域的城市群，每天城市间都发生频繁多样的旅行活动。
• 数据来源与特征：研究使用的是2015年6月8日至14日（周一至周日）台湾地区一周内的出租车载客起点-终点数据，即出租车需求数据。这些旅行覆盖了整个台湾地区。文章通过一些统计图表展示了数据的部分特征，如图2呈现了一周内每小时新产生的出租车出行次数变化情况；图3显示了出行的位移、实际行驶距离和行驶时间的分布情况。同时指出，由于技术难度限制，无法收集所有旅行者的活动数据，因此选择出租车出行作为道路运输的主要方式之一进行研究，期望其发现能为理解城市区域旅行需求提供有益见解，尽管样本不能完全代表总体。

3. Methods（方法）

在“3. Methods（方法）”部分，文章详细介绍了用于构建城市区域旅行需求网络并分析其度分布的方法，具体如下：

3.1 网络构建（Network construction）

空间划分（Spatial partition）

• 将研究的地理空间区域划分成均匀的正方形单元格（cells），每个单元格的边长为L。
• 对于一个面积为ML×NL的区域，总共划分出M·N个单元格。
• 每个单元格用vi表示，其中i∈[1, M·N]。

时间划分（Temporal partition）

• 将一天24小时划分为等大小的时间间隔，每个时间间隔的长度为T。
• 用k表示第k个时间间隔（k∈[1, 24/T]），tk和tk+T分别表示该时间间隔的开始和结束时间。

基于空间-时间划分的有向加权网络构建

• 节点（Node）：每个正方形单元格作为一个节点，即vi。
• 边（Edge）：如果在时间间隔k期间存在从节点vi到vj的旅行，则存在一条从vi到vj的有向边ek_ij。
• 边的权重（Weight）：边的权重wk_ij表示在时间间隔k内从节点vi到vj发生的旅行次数。具体计算公式为：
  $$w_{ij}^k=\sum _{t\in (t_k,t_k+T)}{\text{trip}}_{ij}(t),i\ne j$$
  其中，
  $${\text{trip}}_{ij}(t)=\{\begin{array}{ll}1,& \text{如果在时间t发生了一次从节点vi到vj的旅行}\\ 0,& \text{其他情况}\end{array}$$
• 加权度（Weighted degree）：节点vi的加权度dk是该节点所有边权重的总和，即：
  $$d_k=\sum _{i,j}{w}_{ij}^k$$
• 网络（Network）：构建的时间间隔k的有向加权网络表示为Nk = (V, Ek)，其中V是节点集合，Ek是边集合。

3.2 幂律拟合（Fitting of power laws）

• 幂律的形式为：
  $$p(x)=\alpha x^{-\beta }$$
  其中，α和β是常数，β是幂律指数。
• 对幂律两边取对数，可以得到线性关系：
  $$\ln p(x)=\ln \alpha -\beta \ln x$$
• 为了拟合幂律，首先将经验数据进行对数分箱（logarithmically binned），然后基于最小二乘法（least square method）进行1阶多项式拟合，以确定幂律的参数α和β。

4.Results

4.1 Urban agglomeration travel demand follows a power law（城市区域旅行需求遵循幂律分布）

文章以台湾地区为例，选取了空间-时间划分单元格边长L=1公里、时间间隔T=1小时（下午5:00至6:00）的数据构建旅行需求网络。通过分析发现，该网络的度分布明显遵循幂律，且在一周内相同时间间隔的不同日期，度分布保持不变。利用3.2节介绍的方法测得幂律指数β约为1.89。这一发现表明，城市区域的旅行需求存在层次结构，即大量旅行需求集中在少数发达地区，结构极不平衡。

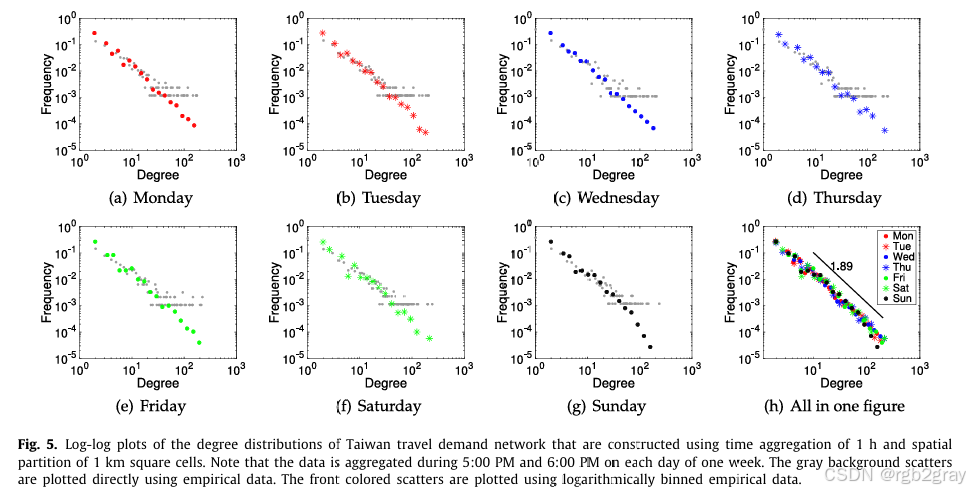
• 图5：展示了旅行需求网络的度分布对数-对数图。图中显示了网络度分布符合幂律的直观证据，即在对数-对数坐标系下，数据点大致排列在一条直线上。灰色背景散点是直接使用经验数据绘制的，而前景彩色散点是使用对数分箱经验数据绘制的。该图验证了城市区域旅行需求网络的度分布具有幂律特性，且这种特性在一周内的相同时间间隔内保持稳定。

4.2 Spatial-temporal fractal of the power law observation（幂律分布的空间-时间分形特性）

4.2.1 Observations（观察）

文章进一步探讨了旅行需求网络的度分布是否受空间划分单元格大小L和时间间隔长度T的影响。研究选取了不同的空间单元格大小（L∈{0.1，0.5，1，2，3，5，10}公里）和时间间隔（T∈{0.25，1，3，6，12}小时），构建了多个旅行需求网络，并测量和拟合每个网络的度分布。结果表明，无论空间和时间粒度如何变化，网络的度分布都遵循幂律，显示出城市区域旅行需求网络具有空间-时间分形特性。所有基于相同大小单元格构建的网络的度分布拟合优度R²均大于0.9，显示出良好的拟合效果。此外，幂律指数随着空间划分单元格大小的增加而单调递减，范围从3.2降至1.4。

• 图6 (a)：展示了不同空间-时间粒度下构建的旅行需求网络的度分布拟合优度R²。图中显示所有R²值均大于0.9，表明无论空间和时间粒度如何变化，旅行需求网络的度分布都很好地符合幂律分布，证实了城市区域旅行需求网络的空间-时间分形特性。
• 图6 (b)：显示了随着空间划分单元格大小L的增加，幂律指数β单调递减的趋势。这表明在进行基于单元格分解的研究时，单元格大小的选择会对结果产生影响，特别是幂律指数会随着单元格的增大而减小。

4.2.2 Reasons of the changes of the power law exponents（幂律指数变化原因）

文章解释了幂律指数随空间划分单元格大小变化的原因。首先，节点的度随着单元格大小的增加而增加，这主要受两个因素影响：一是单元格越大，其周边长度越大，理论上离开该单元格的出行数量可能越多；二是距离需求中心越远，出行数量越少。单元格与需求中心的空间关系可分为两种情况：

• 单元格中心与需求中心重合：在这种情况下，虽然需求中心处需求高，但过小的单元格可能因周边长度小而导致度不高。随着单元格大小增加，度可能先增加后减少。这是因为当单元格增大到一定程度后，虽然周边长度增加，但可能已处于需求较低的区域（如城市边缘），导致度下降。
• 单元格中心偏离需求中心：在这种情况下，随着单元格大小的增加，单元格的边缘更接近需求中心，导致度单调递增。

总体而言，两种情况下单元格的度都随单元格大小增加而增加。
其次，频率随着单元格大小的增加而增加。例如，用小单元格划分区域时，有多个节点具有较低的度；而用大单元格划分同一区域时，有较少节点具有较高的度，导致相同度值的节点频率增加。

• 图7 (a)：展示了单元格中心与需求中心重合的情况。随着单元格大小的增加，度可能先增加后减少，因为虽然需求中心处需求高，但过小的单元格可能因周边长度小而导致度不高，而当单元格增大到一定程度后，虽然周边长度增加，但可能已处于需求较低的区域（如城市边缘），导致度下降。

• 图7 (b)：展示了单元格中心偏离需求中心的情况。随着单元格大小的增加，单元格的边缘更接近需求中心，导致度单调递增。
  

• 图8：在台湾地区任意选取四个点作为中心，其中中心1和2大致与需求中心重合，中心3和4偏离需求中心。这为验证单元格大小对节点度影响的理论分析提供了具体案例。
  

• 图9：展示了以图8中四个中心为基准，不同大小单元格对应的旅行需求网络的度变化情况。数据以2015年6月8日为例计算的小时平均度。图中显示，对于中心1和2，度随单元格大小先增加后减少；对于中心3和4，度随单元格大小单调递增，验证了之前的理论假设。
  

• 图10：直观地展示了单元格大小对节点度频率的影响。使用小单元格划分区域时，有多个节点具有较低的度；而使用大单元格划分同一区域时，有较少节点具有较高的度，导致相同度值的节点频率增加。

通过以上分析，文章得出结论：城市区域旅行需求网络的度分布具有空间-时间分形特性，即无论空间和时间粒度如何变化，网络的度分布都遵循幂律。然而，幂律指数会随着空间划分单元格大小的增加而单调递减，这表明在进行基于单元格分解的研究时，需要谨慎考虑单元格大小对结果的影响。

5. Conclusion（结论）

• 主要发现：以台湾地区为典型城市区域，以出租车需求为代表性旅行需求，通过空间-时间分解构建城市区域旅行需求网络，发现其度分布遵循幂律，并且这种幂律分布不受旅行需求网络构建的空间-时间粒度影响，即城市区域旅行需求具有空间-时间分形特性。但幂律指数会随着划分空间区域的正方形单元格大小的增长而单调递减。
• 研究意义：基于某一地点的出行数量遵循幂律，表明城市区域旅行需求存在层次结构，即大量旅行需求仅从少数发达地区产生，结构极不平衡。这一认识有助于更好地开展城市区域的旅行需求管理和规划。
• 局限性与展望：研究仅考虑了台湾地区这一单一城市区域的数据，且仅使用了出租车数据这一单一数据源，可能存在样本偏差。未来期望利用更多城市区域（如中国的京津冀、欧洲的蓝香蕉地带和金香蕉地带等）的其他数据源（如通话记录数据和火车票数据）反映的旅行需求来增强和丰富本文的研究成果。

6. 其他

import numpy as np
import matplotlib.pyplot as plt
import powerlaw# 生成模拟数据
np.random.seed(42)  # 确保结果可重复# 模拟城市区域的旅行需求度分布
num_nodes = 1000  # 假设城市区域有1000个节点
degrees = np.random.zipf(1.89, num_nodes)  # 使用Zipf分布生成度数据，参数1.89是幂律指数# 绘制度分布的对数-对数图
plt.figure(figsize=(10, 6))
plt.hist(degrees, bins=30, log=True, alpha=0.7, color='blue', edgecolor='black')
plt.xlabel('度 (k)', fontsize=12)
plt.ylabel('频率', fontsize=12)
plt.title('旅行需求网络的度分布 (对数-对数图)', fontsize=14)
plt.xscale('log')
plt.yscale('log')
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.show()# 幂律拟合
fit = powerlaw.Fit(degrees, discrete=True)
alpha = fit.power_law.alpha  # 幂律指数
sigma = fit.power_law.sigma  # 标准差
print(f'幂律指数: {alpha:.2f} (标准差: {sigma:.2f})')# 绘制拟合结果
fig, ax = plt.subplots(figsize=(10, 6))
fit.plot_pdf(color='blue', linewidth=2, label='拟合的幂律分布')
powerlaw.plot_pdf(degrees, color='gray', linestyle='--', alpha=0.7, label='经验分布')
plt.xlabel('度 (k)', fontsize=12)
plt.ylabel('概率密度', fontsize=12)
plt.title('旅行需求网络的度分布与幂律拟合', fontsize=14)
plt.xscale('log')
plt.yscale('log')
plt.legend()
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.show()