机器学习周报-文献阅读
文章目录
- 摘要
- Abstract
- 1 文章内容
- 1.1 Fusion Spatio-temporal Graph Convolution Neural network(FSGCN)
- 1.2 符号和问题陈述
- 1.3 时空特征建模
- 1.3.1 Temporal Attention
- 1.3.2 时空图构建的融合(Fusion of Spatial-Temporal Graph Construction)
- 1.3.3 Spatial-Temporal Embedding
- 1.3.4 图卷积神经网络模块(GCN)
- 1.3.5 Max-Pooling
- 1.3.6 Cropping Operation
- 1.4 时间卷积残差建模
- 1.5 训练过程
- 1.6 实验
- 2 相关代码
- 总结
摘要
本周阅读了题目为Attention-Based Spatiotemporal Graph Fusion Convolution Networks for Water Quality Prediction文章,文章提出了一种融合时空图卷积神经网络(Fusion Spatio-temporal Graph Convolution Neural Network,FSGCN)的时空预测模型,利用时间注意机制来解决水质时间序列的非线性问题;采用图卷积的方法提取河网的空间依赖关系,时空融合更容易捕捉到河网的时空特征;采用时域卷积残差机制,提高了长期序列预测精度。
Abstract
This week, I read an article titled “Attention-Based Spatiotemporal Graph Fusion Convolution Networks for Water Quality Prediction.” The article proposes a spatiotemporal prediction model called the Fusion Spatio-temporal Graph Convolution Neural Network (FSGCN). This model utilizes a temporal attention mechanism to address the nonlinear issues of water quality time series. It employs graph convolution to extract the spatial dependencies of river networks, and the fusion of spatiotemporal features makes it easier to capture the spatiotemporal characteristics of the river networks. Additionally, it adopts a temporal convolution residual mechanism to improve the accuracy of long-term sequence prediction.
1 文章内容
论文题目:Attention-Based Spatiotemporal Graph Fusion Convolution Networks for Water Quality Prediction
链接:https://ieeexplore.ieee.org/document/10471359
现有问题:
- 复杂的非线性关系:水质时间序列数据通常具有复杂的非线性特征,传统的线性模型难以准确预测。
- 空间依赖性:水质监测站点在地理空间上的分布导致数据具有强烈的空间依赖性,需要模型能够捕捉这种空间关系。
- 长期预测精度:现有模型在进行长期预测时,预测精度通常会下降,这影响了模型的实用性
- 特征融合:如何有效地融合时间和空间特征,以提高模型对时空数据的理解和预测能力,是一个挑战。
创新点:
- FSGCN通过调查不同节点之间的上下游关系,预测河网多个节点的未来水质,提高水质预测的准确性。
- FSGCN结合时空融合图的构建,有效地提取水质时间序列的复杂时空特征。
- FSGCN采用时间卷积残差机制,提高了长期序列预测精度。实验表明,FSGCN在预测长期水质时间序列方面优于其典型同行。
1.1 Fusion Spatio-temporal Graph Convolution Neural network(FSGCN)
Fusion Spatio-temporal Graph Convolution Neural network(FSGCN) 是一种用于时空预测任务的深度学习模型,专门设计用于处理具有复杂时空依赖性的数据,例如水质预测、交通流量预测或天气预报等。FSGCN的核心思想是将时间序列数据的空间和时间特征进行有效融合,从而提高预测的准确性和鲁棒性。
FSGCN的主要组成部分:
1. 时间注意力机制(Temporal Attention)
时间注意力机制用于处理时间序列数据中的非线性关系。它通过计算不同时间步之间的依赖强度,为每个时间步分配不同的权重,从而突出重要的时间特征。这种机制能够动态地调整时间序列的输入,使得模型能够更好地捕捉时间序列中的动态变化。
2. 图卷积网络(Graph Convolutional Network, GCN)
GCN是一种用于处理图结构数据的神经网络。在FSGCN中,GCN用于捕捉空间依赖性。例如,在水质预测中,河流网络可以被建模为一个图,其中节点表示监测站,边表示河流的流向。GCN通过聚合邻接节点的信息来更新当前节点的状态,从而能够有效地捕捉空间上的依赖关系。
3. 时空融合技术(Spatiotemporal Fusion)
时空融合技术是FSGCN的核心创新之一。它通过将时间序列数据在多个时间步上的空间特征进行融合,形成一个更大的时空图。这种融合方式使得模型能够同时考虑时间和空间特征,从而更全面地捕捉数据中的时空依赖性。
4. 时间卷积残差模块(Temporal Convolution Residual)
该模块通过时间卷积层提取时间序列信息,并引入残差单元来解决多步预测中的梯度消失问题。这有助于提高模型在长期预测中的准确性和稳定性。
时空融合技术:
时空融合技术是一种将时间和空间特征结合在一起的方法,目的是更全面地捕捉数据中的时空依赖性。在传统的时空预测模型中,时间特征和空间特征通常被分开处理,这可能导致模型无法充分利用数据中的时空关联信息。而时空融合技术通过将时间和空间特征进行整合,使得模型能够同时考虑时间和空间的影响。
1.2 符号和问题陈述

水预测的目的是在给定以前观察到的水质样本收集从N相关的传感器在河流中预测未来的水质。传感器网络表示为
G
=
(
V
,
ε
,
A
)
G=(V,ε,A)
G=(V,ε,A)。
V
V
V表示传感器节点的集合,并且N表示节点的数量。ε表示一组边,
A
∈
R
N
×
N
A∈R^{N×N}
A∈RN×N是网络G的邻接矩阵,表示节点之间的邻近度。例如:
一个河流网络距离的函数,
x
t
i
∈
R
P
x^i_t ∈R^P
xti∈RP表示节点i在时间t的值,其中P表示每个节点的特征的数量。
温度和流速
X
i
=
x
1
i
,
.
.
.
,
x
t
i
,
.
.
.
,
x
T
i
X^i = {{x^i_1,...,x^i_t,...,x^i_T}}
Xi=x1i,...,xti,...,xTi表示从节点i收集的水质的时间序列,并且T表示先前时间步长的数目。
X
=
X
1
,
.
.
.
,
X
t
,
.
.
.
,
X
T
∈
R
N
×
P
×
T
X={X_1,...,X_t,...,X_T}∈R^{N×P×T}
X=X1,...,Xt,...,XT∈RN×P×T表示T个时间步长上所有特征的所有节点的值。
y
^
t
′
\hat y'_t
y^t′表示时间步t中所有节点的预测水质值。
Y
^
=
y
^
1
,
.
.
.
,
y
^
t
′
,
.
.
.
,
y
^
τ
\hat Y ={\hat y_1,...,\hat y'_t,...,\hat y_\tau }
Y^=y^1,...,y^t′,...,y^τ表示在所有结点的时间步
τ
\tau
τ之后得的一系列预测值。
1.3 时空特征建模
1.3.1 Temporal Attention
时间注意力:较长的输入序列会导致预测精度下降。我们采用时间注意力自适应选择相关的输入在所有的时间步骤,并分配不同的权重。
E
E
E表示反映T个时间步之间的时间依赖性的强度的矩阵。
E
p
,
q
E_{p,q}
Ep,q表示
E
E
E的元素。
E
p
,
q
E_{p,q}
Ep,q表示时间步长p和q之间的时间依赖性的强度,其中p,q∈{1,2,· · ·,T}。为了确保注意力权重之和等于1,softmax函数将Ep,q转换为
E
p
,
q
′
E'_{p,q}
Ep,q′。
E
E
E和
E
p
,
q
′
E'_{p,q}
Ep,q′可由下式得到:
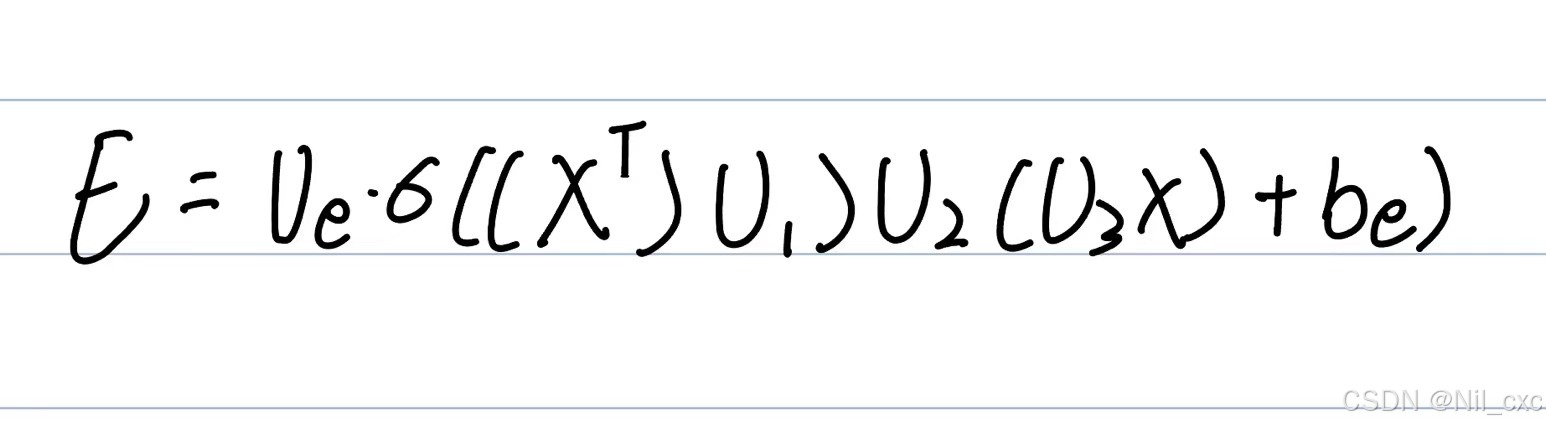
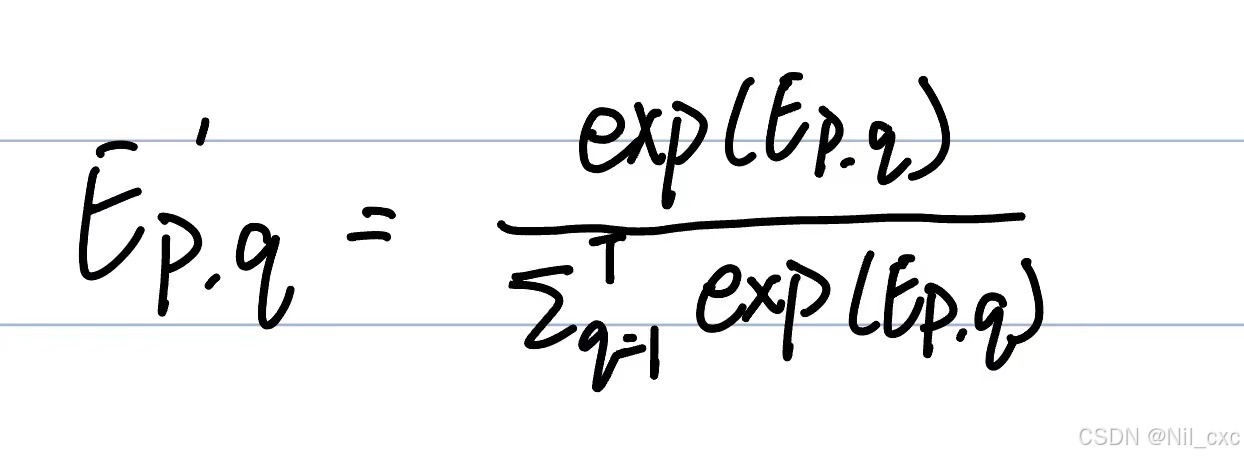
其中, X ∈ R N × P × T X∈R^{N×P×T} X∈RN×P×T表示时间注意的输入, V e , b e ∈ R T × T V_e,b_e∈R^{T×T} Ve,be∈RT×T, U 1 ∈ R N U_1∈R^N U1∈RN, U 2 ∈ R P × T U_2∈R^{P×T} U2∈RP×T和 U 3 ∈ R P U_3∈R^P U3∈RP是时间注意要学习的参数,σ表示激活函数。
E ′ E' E′由softmax函数归一化。最后,我们采用所获得的注意力权重来调整输入 X X X上不同时间步长的权重。
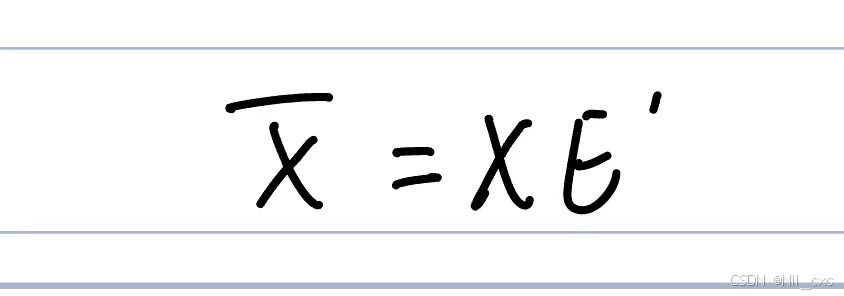
其中 E ′ ∈ R T × T E'∈R^{T×T} E′∈RT×T表示时间注意力权重矩阵,最后得到时间注意力权重处理后的输出 X ^ ∈ R N × T × T \hat X \in R^{N×T×T} X^∈RN×T×T
1.3.2 时空图构建的融合(Fusion of Spatial-Temporal Graph Construction)
捕获每个节点对属于当前和相邻时间步的邻居的影响。通过融合前一时刻的时空图和下一时刻的时空图,获得更大的时空特征视图。放大后的时空图的融合可以更容易地捕捉时空特征和节点之间的关联。
A
′
A'
A′表示融合时空图的邻接矩阵。当两个节点(
v
i
v_i
vi和
v
j
v_j
vj)在空间图中连接时,或者它们在不同时间位于同一节点时,邻接矩阵
A
′
A'
A′中
A
i
,
j
′
A'_{i,j}
Ai,j′的条目设置为1。因此,
A
i
,
j
′
A'_{i,j}
Ai,j′:

其中, v i ( v j ) v_i(v_j) vi(vj)表示节点i(j)。 A ′ ∈ R 3 N × 3 N A'\in R^{3N×3N} A′∈R3N×3N表示在三个连续时间步上构造的图的邻接矩阵。两边的对角线表示属于相邻时间步的每个节点的连通性。
但是用0和1描述邻接矩阵 A ′ A' A′不能有效地表示不同节点的影响程度。为了更好地描述不同节点之间的关系,作者增加了可学习的权重,使关系更加合理。
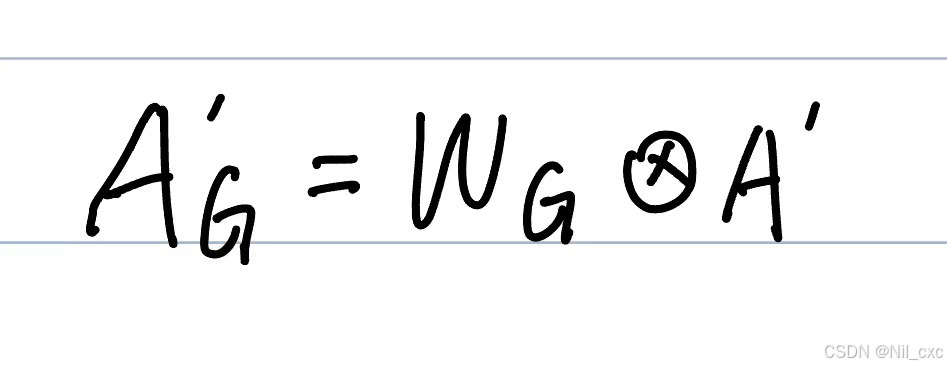
其中
A
′
∈
R
3
N
×
3
N
A'\in R^{3N×3N}
A′∈R3N×3N表示所构造的融合时空图的0-1邻接矩阵。
W
G
W_G
WG表示可学习权重的矩阵。
表示逐元素的乘积运算。
A
G
′
A'_G
AG′表示节点之间的关系矩阵。
1.3.3 Spatial-Temporal Embedding
由于不同时间步长的空间特征都表示在一个融合时空图中,因此需要将空间特征和时间特征分别嵌入,有效地提高了时空特征的相关性。与正弦位置嵌入不同,我们使用可学习的位置嵌入[36]来嵌入时间和空间位置信息。首先,我们初始化可学习的时间嵌入(
T
e
T_e
Te)和空间位置嵌入(
S
e
S_e
Se)。然后,我们使用梯度下降算法来优化嵌入。训练后得到时空位置嵌入。
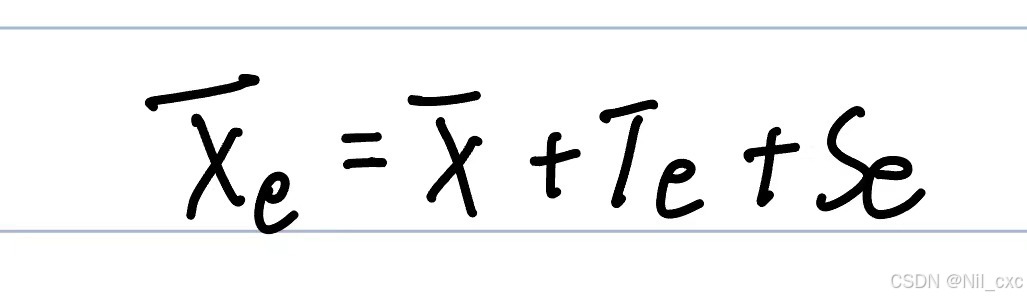
其中 T e ∈ R P × T T_e\in R^{P×T} Te∈RP×T和 S e ∈ R N × P S_e\in R^{N×P} Se∈RN×P分别是嵌入空间和时间特征的矩阵。
1.3.4 图卷积神经网络模块(GCN)
GCN是处理图结构数据的神经网络模型的总称。GCN是一种处理非结构化数据的模型。GCN的最大特点是通过考虑邻居节点的信息来获取单个节点的信息。图中的每个节点都受到其邻居节点的影响并改变其状态,直到达到最终的平衡。关系越密切,邻居的影响力就越大。
在通过时间注意机制处理之后,图卷积操作的输入是融合时空图的矩阵。其中,邻接矩阵采用数字方阵来记录节点之间是否存在连通边,数字代表边的权值。图卷积通过邻接矩阵描述图的节点关系,图卷积运算可以公式化为:

其中 A G ′ ∈ R 3 N × 3 N A'_G\in R^{3N×3N} AG′∈R3N×3N是融合时空图邻接矩阵, h l − 1 ∈ R 3 N × D h^{l−1}\in R^{3N ×D} hl−1∈R3N×D表示图卷积层 l − 1 l−1 l−1的输出,h1 = X <$e是l = 1时的时间注意力输出,W1∈RP×D,W2∈RP×D,b1∈RD和b2∈RD是待学习参数。Sigmoid是一个sigmoid激活函数[37]。最终结果hl被发送到GCN的下一层。
1.3.5 Max-Pooling
为了聚合多层GCN网络,作者采用max操作来处理所有图卷积输出。最大池化操作可以公式化为:
h
M
=
m
a
x
(
h
1
,
h
2
.
.
.
.
,
h
l
)
h_M=max(h^1,h^2....,h^l)
hM=max(h1,h2....,hl)
其中。 h M ∈ R 3 N × D h_M \in R^{3N ×D} hM∈R3N×D
1.3.6 Cropping Operation
在最大池化操作之后,图卷积操作已经聚合了来自多个时间步的信息。为了便于后续计算,我们将联合收割机三个时间步合并为一个时间步。裁剪操作可以公式化为:
X
^
=
σ
(
W
h
h
M
+
b
h
)
\hat X=\sigma(W_hh_M+b_h)
X^=σ(WhhM+bh)
其中X ∈RN×D是裁剪操作的输出。Wh∈RN×3N和bh∈RN是要学习的参数。σ是sigmoid激活函数。
1.4 时间卷积残差建模
作者使用该方法在时间维上采用时间卷积层来获取时间序列的信息。
H
=
R
e
L
U
(
θ
∗
R
e
L
U
(
X
^
)
)
H=ReLU(\theta*ReLU(\hat X))
H=ReLU(θ∗ReLU(X^));其中
H
∈
R
N
×
D
×
T
H∈R^{N×D×T}
H∈RN×D×T表示时间卷积的输出,*表示卷积运算,
θ
\theta
θ表示时间维度的卷积核的参数。ReLU是一个ReLU激活函数。
同时采用残差单元来解决多步预测梯度消失和过拟合的问题。使用LayerNorm计算均值和方差,用于对每个训练案例的求和输入进行归一化。
H
^
=
L
a
y
e
r
N
o
r
m
(
R
e
L
U
(
W
r
X
+
H
)
)
\hat H=LayerNorm(ReLU(W_rX+H))
H^=LayerNorm(ReLU(WrX+H));其中
H
^
∈
R
N
×
D
×
T
\hat H∈R^{N×D×T}
H^∈RN×D×T表示残差的输出,
W
r
W_r
Wr表示需要学习的残差参数矩阵。
时间序列预测模型旨在获得函数F以估计预测值Y。Y的计算公式为:其中
w
y
w_y
wy和
b
y
b_y
by表示权重
Y
^
=
F
(
X
^
1
.
.
.
.
,
X
^
T
)
=
W
y
H
^
+
b
y
\hat Y=F(\hat X_1....,\hat X_T)=W_y\hat H+b_y
Y^=F(X^1....,X^T)=WyH^+by

1.5 训练过程
采用均方误差(MSE)作为损失函数,MSE反映的是预测值 Y ^ ∈ R τ × N \hat Y∈R^{\tau×N} Y^∈Rτ×N与实际值 Y ∈ R τ × N Y∈R^{\tau×N} Y∈Rτ×N之间的误差,即: L = 1 n ∑ i = 1 n ∣ y i − y ^ i ∣ 2 L=\frac{1}{n}\sum^n_{i=1}|y_i-\hat y_i|^2 L=n1∑i=1n∣yi−y^i∣2,同时使用Adam优化器对FSGCN的损失函数进行优化

1.6 实验
1. 实验设置
作者使用阿拉巴马州和京津冀地区的两个真实水质数据集验证了FSGCN的有效性,采用多站溶解氧的历史数据预测未来溶解氧的变化趋势。训练集、验证集和测试集的比例为7:1:2。
数据集:

2. 评估指标
为验证FSGCN的有效性,实验采用3种评价指标计算预测值与真实值之间的误差。分别是平均误差绝对值(MAE)、均方根误差(RMSE)及平均绝对百分误差(MAPE)
3. 基准方法和定量比较
比较FSGCN与ARIMA、ANN、Seq2seq、STGCN、DCRNN、GraphWavenet等基准方法。

由表知在水质数据集的DO的多步时间序列预测中,FSGCN实现了比其他基线模型更高的预测精度。同时,STGCN、DCRNN、GraphWavenet和FSGCN等时空预测模型的预测效果优于Seq2seq、ANN和ARIMA等单节点基线模型,说明时空预测模型在多步预测中优于单节点预测模型。因为时空预测模型使用时空依赖性,而单节点模型仅使用时间信息。 此外,FSGCN显着优于DCRNN和其他时空模型在多步和时空预测。因为FSGCN模型有效地融合了时空特征,而其它模型仅分别接近时间和空间依赖性。
4. 消融实验
FSGCN-nota表示不采用时间注意力。FSGCN-nosp表示删除时空预测模块。FSGCN-noembedding表示不采用时空嵌入。FSGCN-nofusion表示不使用融合时空图结构。
- FSGCN比FSGCN-nota具有更好的性能。原因是时间注意机制捕获了时间序列依赖性。它能有效地处理时间序列中的非线性关系。
- FSGCN优于FSGCN-noembedding,因为时空嵌入可以有效地提取时空特征。
- FSGCN融合时空图建设优于FSGCN-nofusion。
- 不含时空预测模块的FSGCN模型的性能由于空间特征信息的缺乏导致模型的预测能力下降。

2 相关代码
简单实现论文中FSGCN的训练过程
import torch
import torch.nn as nn
import torch.optim as optim
class TemporalAttention(nn.Module):
def __init__(self, input_dim, hidden_dim):
super(TemporalAttention, self).__init__()
self.W1 = nn.Linear(input_dim, hidden_dim)
self.W2 = nn.Linear(hidden_dim, hidden_dim)
self.W3 = nn.Linear(hidden_dim, 1)
self.softmax = nn.Softmax(dim=1)
def forward(self, x):
# x shape: (batch_size, num_nodes, num_features, num_timesteps)
x = x.permute(0, 2, 3, 1) # Reshape to (batch_size, num_features, num_timesteps, num_nodes)
e = self.W1(x)
e = torch.tanh(e + self.W2(e.permute(0, 1, 3, 2)).permute(0, 1, 3, 2))
e = self.W3(e)
alpha = self.softmax(e, dim=2) # Apply softmax along the num_timesteps dimension
weighted_x = x * alpha.unsqueeze(1) # Ensure alpha has the same number of dimensions as x
return weighted_x.sum(dim=2) # Sum along the num_timesteps dimension
class SpatioTemporalGraphConstruction(nn.Module):
def __init__(self, num_nodes, num_features):
super(SpatioTemporalGraphConstruction, self).__init__()
self.W = nn.Linear(num_features, num_features)
def forward(self, x):
# Assuming x is of shape (batch_size, num_nodes, num_features)
adj_matrix = torch.sigmoid(self.W(x))
return adj_matrix
class SpatialTemporalEmbedding(nn.Module):
def __init__(self, num_nodes, num_features, embedding_dim):
super(SpatialTemporalEmbedding, self).__init__()
self.temporal_embedding = nn.Linear(num_features, embedding_dim)
self.spatial_embedding = nn.Linear(num_nodes, embedding_dim)
def forward(self, x):
temporal_emb = self.temporal_embedding(x)
spatial_emb = self.spatial_embedding(torch.ones(x.size(1), device=x.device)).unsqueeze(0).repeat(x.size(0), 1, 1)
return x + temporal_emb + spatial_emb
class GCN(nn.Module):
def __init__(self, input_dim, hidden_dim):
super(GCN, self).__init__()
self.conv = nn.Conv2d(input_dim, hidden_dim, kernel_size=(1, 1))
def forward(self, adj_matrix, x):
x = x.permute(0, 3, 1, 2) # Reshape for convolution
x = torch.matmul(adj_matrix.unsqueeze(1), x) # Add a channel dimension for broadcasting
x = x.permute(0, 2, 3, 1) # Reshape back
return torch.relu(self.conv(x))
class TemporalConvolutionResidual(nn.Module):
def __init__(self, input_dim, hidden_dim):
super(TemporalConvolutionResidual, self).__init__()
self.conv = nn.Conv1d(input_dim, hidden_dim, kernel_size=3, padding=1)
self.layer_norm = nn.LayerNorm(hidden_dim)
def forward(self, x):
residual = x
x = torch.relu(self.conv(x))
x = self.layer_norm(x + residual)
return x
class FSGCN(nn.Module):
def __init__(self, num_nodes, num_features, hidden_dim):
super(FSGCN, self).__init__()
self.temporal_attention = TemporalAttention(num_features, hidden_dim)
self.spatio_temporal_graph_construction = SpatioTemporalGraphConstruction(num_nodes, num_features)
self.spatial_temporal_embedding = SpatialTemporalEmbedding(num_nodes, num_features, hidden_dim)
self.gcn = GCN(num_features, hidden_dim)
self.max_pooling = nn.MaxPool1d(2)
self.cropping = nn.Linear(2 * hidden_dim, hidden_dim)
self.temporal_convolution_residual = TemporalConvolutionResidual(hidden_dim, hidden_dim)
def forward(self, x):
batch_size, num_nodes, num_features, num_timesteps = x.size()
x = self.temporal_attention(x)
adj_matrix = self.spatio_temporal_graph_construction(x)
x = self.spatial_temporal_embedding(x)
h = self.gcn(adj_matrix, x)
h = self.max_pooling(h)
x = self.cropping(h)
y_hat = self.temporal_convolution_residual(x)
return y_hat
# Example usage
num_nodes = 10
num_features = 5
hidden_dim = 20
num_timesteps = 10
batch_size = 32
# Initialize model
model = FSGCN(num_nodes, num_features, hidden_dim)
# Initialize data
x = torch.randn(batch_size, num_nodes, num_features, num_timesteps)
y = torch.randn(batch_size, num_nodes, num_timesteps)
# Define loss function and optimizer
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
# Train model
for epoch in range(100):
optimizer.zero_grad()
y_hat = model(x)
loss = criterion(y_hat, y)
loss.backward()
optimizer.step()
print(f'Epoch {epoch+1}, Loss: {loss.item()}')
总结
该论文设计了FSGCN模型预测水质,采用时间注意力机制捕捉动态、融合时空特征,用GCN探究河网空间依赖关系,整合时间卷积和残差单元提升长期预测性能。
