当前位置：首页 > news >正文

leetcode--接雨水（双指针法，动态规划，单调栈）

news 来源：原创 2025/4/27 10:12:34

方法一：双指针法

方法二：动态规划

方法三：单调栈

42. 接雨水 - 力扣（LeetCode）

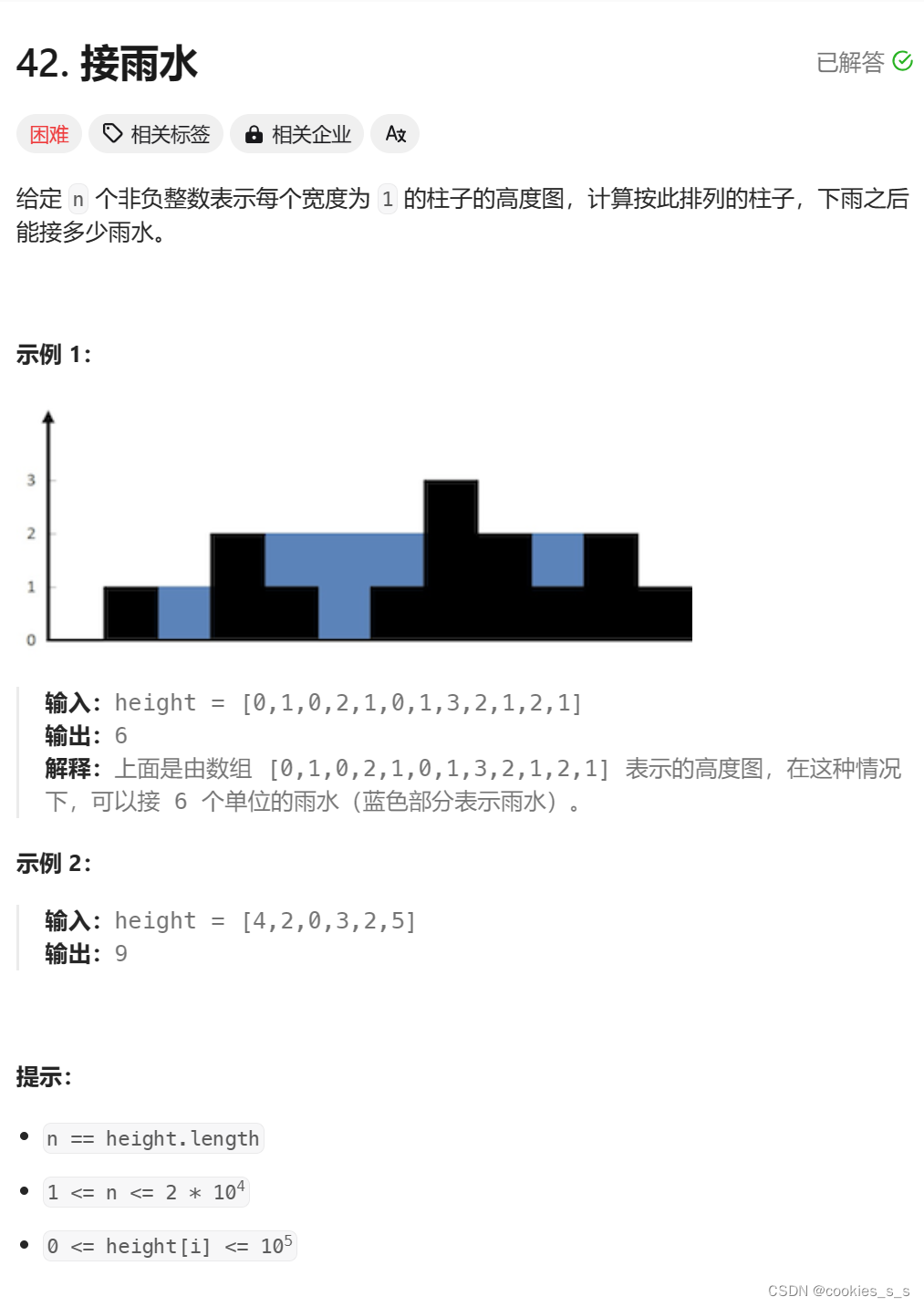
黑色的是柱子，蓝色的是雨水，我们先来观察一下雨水的分布情况:
雨水落在凹槽之间，在一个凹槽的左右都会有两个柱子，两个柱子高度可能相同也可能不同，柱子的高低决定了凹槽的雨水的高度，雨水的高度等于两个柱子较低的高度。

方法一：双指针法

时间复杂度：O（N^2）;

空间复杂度：O(1)；

缺点：会超时;

思想：统计各个所在位置的左边最高高度和右边最高位置（第一个和最后一个柱子所在位置不用统计，他们不可能会接收雨水），然后算出各个位置雨水面积（两边的最高高度的较小值 - 当前位置的柱子的面积），最后将各个位置的面积相加得到总面积。

具体实现：

class Solution {
public:
    int trap(vector<int>& height) {
        //面积和
        int sum = 0;
        for(int i = 0; i < height.size(); i++)
        {
            //第一个和最后一个不用统计
            if(i == 0 || i == height.size() - 1)
            continue;
            int maxLeft = height[i];
            int maxRight = height[i];
            //统计右边
            for(int j = i + 1; j < height.size(); j++)
            {
                maxRight = max(maxRight,height[j]);
            }
            //统计左边
            for(int j = i - 1; j >= 0; j--)
            {
                maxLeft = max(maxLeft,height[j]);
            }
            //高度计算
            int h = min(maxLeft,maxRight) - height[i];
            if(h > 0)
            sum += h;
        }
        return sum;
    }
};

方法二：动态规划

时间复杂度为 O(N)；

空间复杂度为 O(N);

思路：在方法一的基础上我们知道，只要知道各个位置的左右最高高度，通过计算就可以求得各个位置的面积，再相加就可以得到总面积。所以就需要遍历数组来找到左右最高高度，方法一使用双指针来求左右最高高度，每走到柱子位置就向左右方向进行统计，实际上是进行了重复计算的，导致时间复杂度为O(N^2)。因为柱子的位置都不会变，对于每个柱子，相对的左右最高高度也是不会变的，所以只需要遍历两次，把每个位置的左右最高高度计算出来放在两个数组中，最后再计算面积就行了。

class Solution {
public:
    int trap(vector<int>& height) {
        //动态规划做法
        //小于等于2个直接返回
        if(height.size() <= 2)
        return 0;
        //左边最高高度--数组初始化为0
        vector<int> maxLeft(height.size(),0);
        //右边最高高度--数组初始化为0
        vector<int> maxRight(height.size(),0);
        //遍历一次数组记录各个位置的左边最高高度
        maxLeft[0] = height[0];
        for(int i = 1; i < maxLeft.size(); i++)
        {
            maxLeft[i] = max(height[i],maxLeft[i - 1]);
        }
        //遍历一次数组记录各个位置的右边最高高度
        maxRight[maxRight.size() - 1] = height[height.size() - 1];
        for(int i = maxRight.size() - 2; i >= 0; i--)
        {
            maxRight[i] = max(height[i],maxRight[i + 1]);
        }
        //求和
        int sum = 0;
        for(int i = 0; i < height.size(); i++)
        {
            int count = min(maxLeft[i],maxRight[i]) - height[i];
            if(count > 0)
            {
                sum += count;
            }
        }
        return sum;
    }
};

方法三：单调栈

空间复杂度：O(n)；

时间复杂度：O(n)；

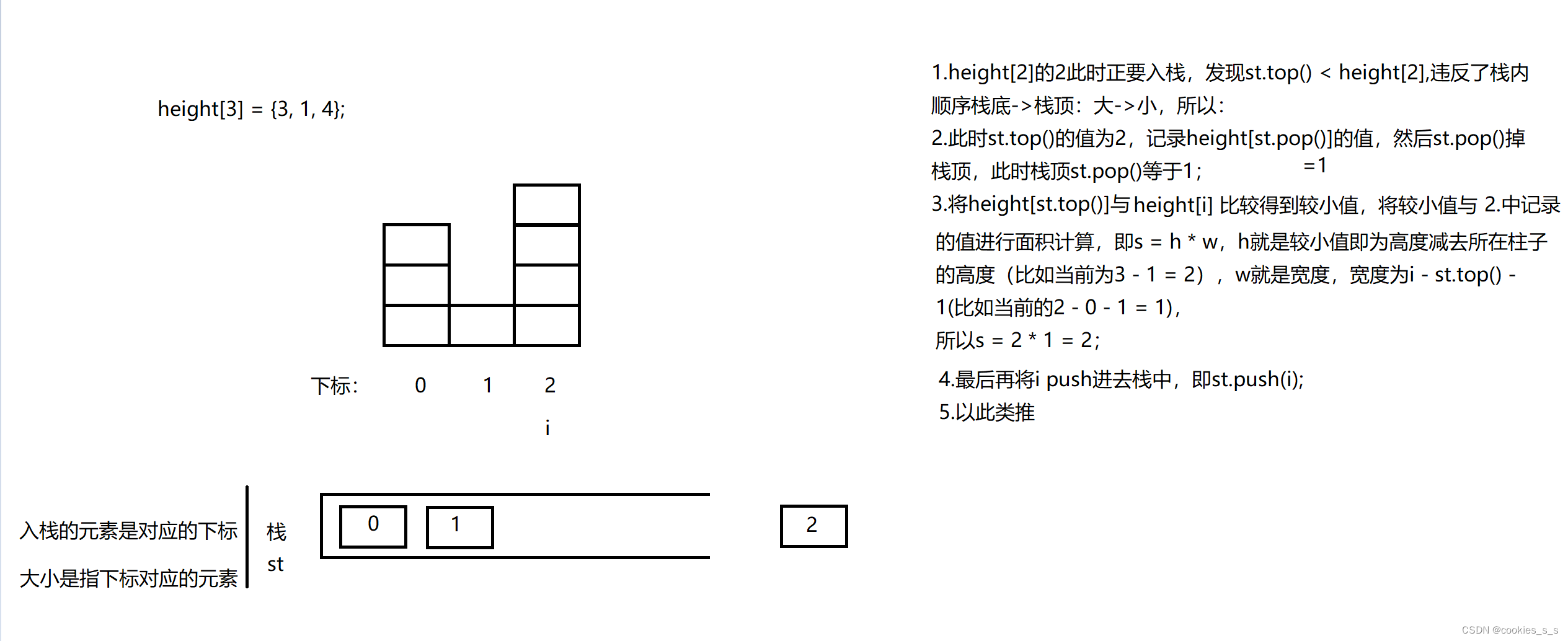
使用单调栈使站内元素有序，然而单调栈没有现成的容器，所以需要我们自己维持元素有序；

那么栈内有序是（栈底->栈顶）小->大还是大->小呢？答案是大->小；当下一个柱子高度小于栈顶元素时就入栈，就能维持栈内有序，当遇到下一个柱子高度大于栈顶元素时就将栈顶pop掉，再将当前的栈顶元素与下一个柱子的高度比较就可以得到较小值，然后就和上面一样计算面积了。

class Solution {
public:
    int trap(vector<int>& height) {
        //如果数组个数两个及以下，直接return
        if(height.size() <= 2)
        return 0;
        //创建单调栈（栈顶->栈底==小->大），存放下标值
        stack<int> st;
        st.push(0);
        //统计面积
        int sum = 0;
        //行方向计算
        for(int i = 1; i < height.size(); i++)
        {
            //1.下一个元素小于栈顶元素
            if(height[i] < height[st.top()])
            {
                st.push(i);
            }
            //2.下一个元素等于栈顶元素--pop栈顶元素的下标，push下一个元素的下标
            else if(height[i] == height[st.top()])
            {
                st.pop();
                st.push(i);
            }
            //3.下一个元素大于栈顶元素--形成凹槽接收雨水，计算雨水面积
            else
            {
                while(!st.empty() && height[i] > height[st.top()])
                {
                    //中间的凹槽下标
                    int mid = st.top();
                    st.pop();
                    if(!st.empty())
                    {
                        //高度计算
                        int h = min(height[st.top()],height[i]) - height[mid];
                        //宽度计算
                        int w = i - st.top() - 1;
                        //面积
                        sum += h * w;
                    }
                }
                st.push(i);
            }
        }
        return sum;
    }
};