当前位置：首页 > news >正文

力扣最热一百题——二叉搜索树中第 K 小的元素

news 来源：原创 2025/4/19 7:47:54

题目链接：230. 二叉搜索树中第 K 小的元素 - 力扣（LeetCode）

题目描述

进阶问题

1. 使用带节点计数的增强型二叉搜索树

思路：

实现细节：

算法步骤：

2. 使用平衡二叉搜索树（如 AVL 树、红黑树）

3. 使用其他数据结构（如跳表、B+ 树）

什么是二叉搜索树

操作

特性与应用

解法一：中序遍历

代码说明：

示例输入输出：

Java写法：

C++写法：

运行时间

时间复杂度和空间复杂度

总结

题目链接：230. 二叉搜索树中第 K 小的元素 - 力扣（LeetCode）

注：下述题目描述和示例均来自力扣

题目描述

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 小的元素（从 1 开始计数）。

示例 1：

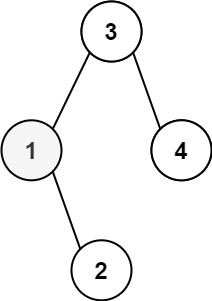
输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

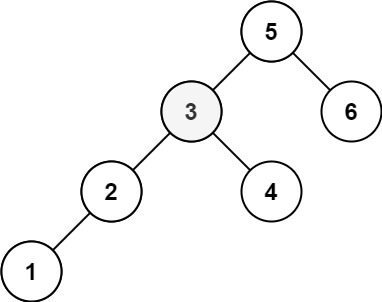
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

提示：

树中的节点数为 n 。
1 <= k <= n <= 10^4
0 <= Node.val <= 10……4

进阶问题

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

当二叉搜索树（BST）频繁被修改（插入/删除操作），并且需要频繁地查找第 k 小的值时，普通的中序遍历方法可能不再高效。因为每次查找都需要重新遍历树，时间复杂度为 O(h + k)，其中 h 是树的高度。如果树不平衡，性能会进一步下降。

为了优化这种情况，我们可以引入一些额外的数据结构或策略来减少重复计算。以下是几种常见的优化方法：

1. 使用带节点计数的增强型二叉搜索树

思路：

在每个节点中维护一个额外的字段 size，表示以该节点为根的子树中节点的总数（包括当前节点）。这样可以快速定位第 k 小的元素，而无需每次都进行完整的中序遍历。

实现细节：

每个节点增加一个 size 字段。
插入和删除操作时，更新相关路径上的 size 值。
查找第 k 小的元素时，利用 size 字段直接确定目标节点的位置。

算法步骤：

如果左子树的 size 大于等于 k，说明第 k 小的元素在左子树中，递归进入左子树。
如果左子树的 size 加上当前节点正好等于 k，则当前节点就是第 k 小的元素。
否则，第 k 小的元素在右子树中，递归进入右子树，并将 k 减去左子树的 size 和当前节点的 1。

2. 使用平衡二叉搜索树（如 AVL 树、红黑树）

如果树经常被修改且不保证平衡性，树可能会退化成链表，导致性能下降。因此，使用自平衡的二叉搜索树（如 AVL 树或红黑树）可以确保树的高度始终保持在 O(log n)。

结合上述增强型 BST 的思想，在自平衡树中维护 size 字段，可以在 O(log n) 时间内完成插入、删除和查找第 k 小的操作。

3. 使用其他数据结构（如跳表、B+ 树）

对于更复杂的场景（例如大规模数据存储），可以考虑使用其他支持动态排序和范围查询的数据结构，例如跳表（Skip List）或 B+ 树。这些数据结构通常用于数据库系统和文件系统，能够更好地处理频繁的插入、删除和查询操作。

什么是二叉搜索树

二叉搜索树（Binary Search Tree, BST），也称为有序二叉树（ordered binary tree）或排序二叉树（sorted binary tree），是一种特殊的二叉树数据结构，它具有以下特性：

节点值的顺序：
- 每个节点包含一个键（key）、一个关联的值、一个指向左子树的引用和一个指向右子树的引用。
- 节点的键大于左子树中任意节点的键。
- 节点的键小于右子树中任意节点的键。
左右子树也是二叉搜索树：
- 除了根节点外，每个节点本身也是一个二叉搜索树，包括其所有的属性和规则。
没有重复的键：
- 通常情况下，二叉搜索树不允许存在重复的键。不过，在某些实现中可以通过特定方式存储重复的键。

操作

查找（Search）：从根节点开始，如果目标值等于节点的键，则找到；如果目标值较小，则在左子树中继续查找；如果较大，则在右子树中查找。这个过程递归进行，直到找到匹配的节点或者到达叶节点为止。
插入（Insert）：类似于查找操作，首先定位到应该插入的位置，然后创建一个新的节点作为该位置的子节点。
删除（Delete）：较为复杂，分为三种情况：
- 删除的节点是叶节点：直接移除该节点。
- 删除的节点只有一个孩子：将该节点与其子节点连接起来，然后移除该节点。
- 删除的节点有两个孩子：可以使用该节点的前驱（in-order predecessor）或后继（in-order successor）来替换它，然后再删除前驱或后继节点。
遍历（Traversal）：有多种遍历方式，如前序遍历（Pre-order Traversal）、中序遍历（In-order Traversal）、后序遍历（Post-order Traversal）。其中，中序遍历会按照升序访问所有节点，这是由BST的性质决定的。

特性与应用

高效的数据检索：由于其结构特点，使得查找、插入和删除操作的时间复杂度平均为O(log n)，但在最坏的情况下（如树退化成链表时）这些操作的时间复杂度可能达到O(n)。
平衡性问题：为了保证高效的性能，需要保持树的平衡。因此出现了诸如AVL树、红黑树等自平衡二叉搜索树。

二叉搜索树广泛应用于数据库和文件系统中的索引结构，以及需要快速查找、插入和删除数据的应用场景。通过保持树的平衡，可以确保在大多数情况下操作都是高效的。

解法一：中序遍历

在二叉搜索树（BST）中，中序遍历会按照从小到大的顺序访问节点。因此，我们可以通过对 BST 进行中序遍历，在遍历过程中记录当前访问的节点数，当访问到第 k 个节点时，返回其值即可。

代码说明：

TreeNode 类：定义了二叉树的节点结构。
kthSmallest 方法：
- 使用栈实现非递归的中序遍历。
- 遍历过程中用 count 记录当前访问的节点数。
- 当 count == k 时，返回当前节点的值。
主函数：
- 构造了一个示例二叉搜索树，并调用 kthSmallest 方法查找第 k 小的元素。

示例输入输出：

假设二叉搜索树如下：

       5/ \3   6/ \2   4/1

如果 k = 3，则输出为：3

Java写法：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int kthSmallest(TreeNode root, int k) {// 使用栈来模拟中序遍历Stack<TreeNode> stack = new Stack<>();TreeNode current = root;int count = 0;while (current != null || !stack.isEmpty()) {// 先将左子树的所有左节点压入栈while (current != null) {stack.push(current);current = current.left;}// 弹出栈顶元素current = stack.pop();count++;// 如果是第 k 个元素，直接返回if (count == k) {return current.val;}// 转向右子树current = current.right;}}
}

C++写法：

#include <iostream>
#include <stack>using namespace std;// 定义二叉树节点结构
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};class Solution {
public:int kthSmallest(TreeNode* root, int k) {// 使用栈来模拟中序遍历stack<TreeNode*> stk;TreeNode* current = root;int count = 0;while (current != nullptr || !stk.empty()) {// 先将左子树的所有左节点压入栈while (current != nullptr) {stk.push(current);current = current->left;}// 弹出栈顶元素current = stk.top();stk.pop();count++;// 如果是第 k 个元素，直接返回if (count == k) {return current->val;}// 转向右子树current = current->right;}// 如果没有找到第 k 小的元素，抛出异常throw invalid_argument("Invalid input or k is out of range");}
};int main() {// 构建一个示例二叉搜索树TreeNode* root = new TreeNode(5);root->left = new TreeNode(3);root->right = new TreeNode(6);root->left->left = new TreeNode(2);root->left->right = new TreeNode(4);root->left->left->left = new TreeNode(1);Solution solution;int k = 3;cout << "第 " << k << " 小的元素是: " << solution.kthSmallest(root, k) << endl;return 0;
}