动态规划入门:4种背包问题大纲
背包不一定要装满,背包容量一定,为V
N个物品,每个物品有wi价值、vi体积,问装备方法使得总价值最大
目录
概述:
一、0-1背包问题
为什么0-1背包问题滚动数组法体积j要从大到小枚举:
二、完全背包问题
1.按顺序枚举方法:
2.优化方法:
3.一维从小到大枚举体积j滚动数组写法:
为什么完全背包问题滚动数组法体积j要从小到大枚举:
三、多重背包问题
1.顺序枚举法:
2.分析f数组元素意义后简化对比次数法:
四、分组背包问题
五、针对滚动数组写法小结
概述:
①0-1背包问题
每个物品最多使用一次
②完全背包问题
每个物品最可使用无数次,但是每个物品数量要保证k*v[i]<=j体积的k个
③多重背包问题
不同种物品数量不同且有限
④分组背包问题
多个物品分别分组,一组只能选一次
一、0-1背包问题


| Dp问题 | 状态表示 f(i,j) (与wi价值同量纲) | 集合 | 所有选法 | - |
| 条件 | ①只从前 i 个物品种选 ②总体积 ≤ j | |||
| 属性 | (max、min、数量等) | - | ||
| - | ||||
| 状态计算 | 集合划分 | 不含第i个物品 | f(i-1,j) | |
| - | ||||
| 含第i个物品 | f(i-1,j-vi)+wi | |||
| - |
最终 f(i,j) = max( f( i-1 , j ) , f( i-1 , j-vi ) + wi )
上面标红的地方是个重点编码技巧所在,你可以认为f(i,j)也是叫含第i个物品不超过j体积,那标红的部分也可以这么
二维表示法:
#include<iostream>
#include<algorithm>
using namespace std;const int N=1010;
int f[N][N];
int v[N],w[N];
int n,m;
int main()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>v[i]>>w[i];//第几个物品只能从1开始for(int i=1;i<=n;i++)//有等于,包括第i个物品,第几个物品只能从1开始{for(int j=0;j<=m;j++)//有等于包括体积为j、0{f[i][j]=f[i-1][j];//不包括第i个物品if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);//与原本f[i][j]作对比,看加第i个物品是的价值是多了还是少了//max函数第二个位置的编写是动态规划中最核心技巧。//总集合划分为第i个选或不选,max第一个变量为第i物品不选的划分,第二个变量为第i个物品选的划分}}cout<<f[n][m];return 0;}一维表示法(j体积从后往前缩小到v[i]的滚动数组):
#include<iostream>
#include<algorithm>
using namespace std;const int N=1010;
int n,m;int v[N],w[N];
int f[N];//下标表示总体积,内容表示价值int main()
{cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=m;j>=v[i];j--)//重点{f[j]=max(f[j],f[j-v[i]]+w[i]);}}cout<<f[m]<<endl;
}为什么0-1背包问题滚动数组法体积j要从大到小枚举:
会导致重复选择同一物品


二、完全背包问题

| Dp问题 | 状态表示 f(i,j) (与wi价值同量纲) | 集合 | 所有选法 | - |
| 条件 | ①只从前 i 个物品种选 ②总体积 ≤ j | |||
| 属性 | (max、min、数量等) | - | ||
| - | ||||
| 状态计算 | 集合划分 | 第i个物品0个 | f(i-1,j) | |
| - | ||||
| 第i个物品选1、2、3...k个 | f(i-1,j-k*vi)+k*wi | |||
| - |
然而以上两个状态的计算方程可以合并为f(i,j) =max( f(i,j) , f( i-1 , j-k*vi ) + k*wi )
1.按顺序枚举方法:
不重不漏的保证方法:第i个不选体积为j、第i个选k个(k=0、1...k)体积为 j-k*v[i]
#include<iostream>
#include<algorithm>
using namespace std;const int N=1010;
int f[N][N];
int v[N],w[N];
int n,m;int main()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){for(int k=0;k*v[i]<=j;k++){f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);}}}cout<<f[n][m];
}2.优化方法:
考虑f[i][j]、f[i][j-v]元素的意义
 实际上需要比较的只有f[i-1][j]与f[i][j-v]+w[i]元素两者取max
实际上需要比较的只有f[i-1][j]与f[i][j-v]+w[i]元素两者取max
 因此,f(i,j)只和两项有关,无需用k进行遍历操作。
因此,f(i,j)只和两项有关,无需用k进行遍历操作。
#include<iostream>
#include<algorithm>
using namespace std;const int N=1010;
int f[N][N];
int v[N],w[N];
int n,m;int main()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){f[i][j]=f[i-1][j];if(j>=v[i])f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);}}cout<<f[n][m];
}与0-1背包问题的区别在于第二项的状态转移是从i-1转移过来还是从i转移过来,还要注意这个代码是推导式,直觉不太能直接进行理解,完全背包问题的简化代码一定是推导出来的,但的确有一步是从前一个状态转过来的过程f[i][j]=f[i-1][j]即第i个不选的情形;逻辑上有滚动数组的意思,即不需要每轮都全部枚举只需要每轮按需保证在整个过程中每种选择情形被对比一次即可。
0-1背包问题代码片段:

0-1背包问题第二项是从i-1转移过来(上为0-1背包问题,下为完全):

最后还要说一下,能如此优化的大前提就是f[i][j]中的每个元素都是各轮最大值,从而保证了可以滚动。
3.一维从小到大枚举体积j滚动数组写法:
#include<iostream>
#include<algorithm>
using namespace std;const int N=1010;
int f[N];
int v[N],w[N];
int n,m;int main()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=v[i];j<=m;j++){f[j]=max(f[j],f[j-v[i]]+w[i]);}}cout<<f[m];
}0-1背包问题和完全背包问题的滚动数组版本最后就只差在了前者体积从大到小枚举,后者体积从小到大枚举,想清楚这个区别与两问题特点之间的关系
为什么完全背包问题滚动数组法体积j要从小到大枚举:
若完全背包问题体积从大到小枚举则会导致无法多次选择同一物品:


三、多重背包问题
每个物品有限si个

| Dp问题 | 状态表示 f(i,j) (与wi价值同量纲) | 集合 | ①只从前 i 个物品种选 ②总体积 ≤ j | - |
| - | ||||
| 属性 | max | - | ||
| - | ||||
| 状态计算 | 集合划分 | 不含第i个物品 | f(i-1,j) | |
| - | ||||
| 含第i个物品 | f(i-1,j-k*vi)+k*wi | |||
| k<=s[i] |
与0-1背包问题作对比,发现在0-1背包问题中需要先进行f[i][j]=f[i-1][j]的赋值操作,但是后面完全背包问题多重背包问题的顺序枚举方法中没有这一步先行赋值操作,为什么?
0-1背包问题代码片段:

完全背包问题代码片段:
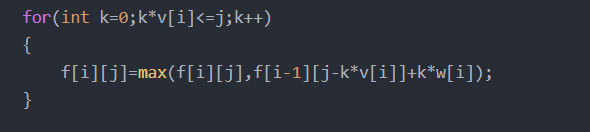
因为在k=0时蕴含了与f[i][j]=f[i-1][j]的比较操作
1.顺序枚举法:
#include <iostream>
#include <algorithm>
using namespace std;
const int N=110;
int f[N][N];
int s[N],v[N],w[N];
int n,m;int main()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>v[i]>>w[i]>>s[i];for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){for(int k=0;k*v[i]<=j&&k<=s[i];k++){f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);}}}cout<<f[n][m];
}
2.分析f数组元素意义后简化对比次数法:


C++1s内最多完成10^7~10^8次计算,本题N*V*S优化为N*V*logS ,1000*2000*log2000≈2*10^7在范围内。
f[i][j]与完全背包问题的元素意义略有区别:
二进制优化:
例如我想用二进制加减来凑出200以内的所有数只需要以下几个数加减即可


#include<iostream>
#include<algorithm>
using namespace std;const int N=25000;//N种物品,每种物品数量使用二进制指数加减生成1000*log2000约2万个
int v[N], w[N];
int f[N];int main()
{int n, m;cin >> n >> m;//物品种类、背包体积int cnt = 0;//最外层循环是不同种物品,一轮外循环内部只有一种物品按照数量作划分for (int i = 1; i <= n; i++){int a, b, s;//a价值b重量s数量cin >> a >> b >> s;int k = 1;//幂块//划分while (k <= s){cnt++;//块内该种物品总体积、总价值v[cnt] = a * k;w[cnt] = b * k;//块的划分s -= k;k *= 2;}//bias尾块if (s > 0){cnt++;v[cnt] = a * s;w[cnt] = b * s;}}n = cnt;//n种物品整体为一个类别,总数量重新划分为cnt块//不同种类的物品对应下标cnt不一样,同种物品不同数量块的cnt下标也不一样不必担心for (int i = 1; i <= n; i++)for (int j = m; j >= v[i]; j--)f[j] = max(f[j], f[j - v[i]] + w[i]);cout << f[m] << endl;return 0;
}四、分组背包问题

| Dp问题 | 状态表示 f(i,j) (与wi价值同量纲) | 集合 | ①只从前 i 个物品种选 ②总体积 ≤ j | - |
| - | ||||
| 属性 | max | - | ||
| - | ||||
| 状态计算 | 集合划分 | 不含第i个物品 | f(i-1,j) | |
| - | ||||
| 枚举第i种物品,类内选哪一 个 | f(i-1,j-v(i,k))+w(i,k) | |||
| - |
#include<iostream>
#include<algorithm>
using namespace std;const int N=110;
int f[N],s[N];
int v[N][N],w[N][N];
int n,m;//将大小n和v数组与m总体积区分开来
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>s[i];for(int j=1;j<=s[i];j++){cin>>v[i][j]>>w[i][j];}}for(int i=1;i<=n;i++){//利用的是上一轮的状态,背包体积从大到小枚举for(int j=m;j>=1;j--)//这里j到0和到1对结果没有影响{for(int k=1;k<=s[i];k++)if(j>=v[i][k])f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);}}cout<<f[m];}五、针对滚动数组写法小结
用的是上一轮的状态则从大到小枚举体积,用的是本轮的状态的话则从小到大枚举体积
