笔试专题（十一）

添加字符（暴力枚举）

题目链接

题解

1. 暴力枚举
2. 固定b串的位置，a串每次从0开始枚举，统计不相等的字符个数，求不相等字符个数的最小值，其他位置都可以添加为相等的字符

代码

#include <iostream>
#include<string>
using namespace std;int main()
{string a,b;cin >> a >> b;int n = a.size();int m = b.size();   int ret = n;for(int i = 0;i <= m - n;i++)// b串 {int tmp = 0;for(int j = 0;j < n;j++)// a串{if(b[i+j] != a[j]){tmp++;}}ret = min(ret,tmp);}cout << ret << '\n';return 0;
}

城市群数量（dfs）

题目链接

题解

1. 使用dfs，图的遍历
2. 计算联通块的数量，一次dfs，标记走过的数值为1的点标记为true，ret++，然后找下一个值为1的点继续遍历，最终统计出所有的联通块

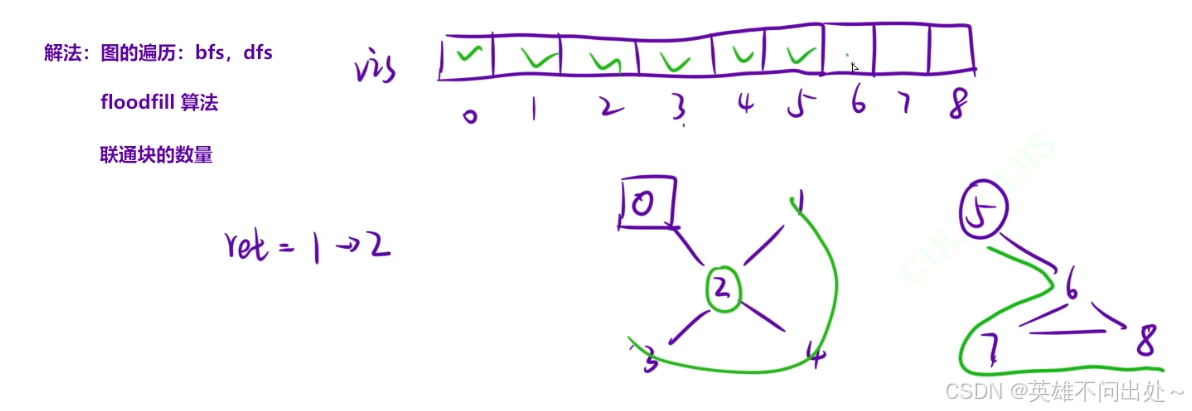
代码

class Solution 
{
public:bool vis[210] = {0};int citys(vector<vector<int>>& m) {// 用dfs计算联通块的数量,图的遍历int n = m.size();int ret = 0;for(int i = 0;i < n;i++){if(!vis[i]) {ret++;dfs(m,i);}}return ret;}void dfs(vector<vector<int>>& m,int pos){vis[pos] = true;for(int i = 0;i < m.size();i++){if(!vis[i] && m[pos][i]){dfs(m,i);}}}
};

判断是不是平衡二叉树（递归）

题目链接

题解

1. 左右子树的节点的个数肯定大于等于0，因此返回值为int，-1既表示返回bool表示每个节点是否是平衡二叉树，又表示该节点的高度
2. 如果返回-1表示该树不是平衡二叉树，否则是平衡二叉树
3. 只需考虑当前节点在干什么就可以写出递归

代码

/*** struct TreeNode {*	int val;*	struct TreeNode *left;*	struct TreeNode *right;*	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* };*/
class Solution 
{
public:int dfs(TreeNode* root){if(root == nullptr) return 0;int left = dfs(root->left);if(left == -1) return -1;// 剪枝int right = dfs(root->right);if(right == -1) return -1;return abs(left-right) <= 1 ? max(left,right) + 1: -1;}bool IsBalanced_Solution(TreeNode* pRoot) {return dfs(pRoot) != -1;}
}; 

最大子矩阵（二维前缀和）

题目链接

题解

1. 忘记考虑x2，y2 比 x1，y1大的问题了
2. 枚举出所有的情况需要四层for循环

代码

#include <iostream>
using namespace std;int a[110][110];
int pre[110][110];int main()
{int n;cin >> n;for(int i = 1;i <= n;i++){for(int j = 1;j <= n;j++){cin >> a[i][j];}}for(int i = 1;i <= n;i++){for(int j = 1;j <= n;j++){pre[i][j] = pre[i-1][j] + pre[i][j-1] - pre[i-1][j-1] + a[i][j];}}// x2,y2必须比x1,y1大,开始的时候没考虑到这一点int ans = -110;int k = 0;for(int x1 = 1;x1 <= n;x1++){for(int y1 = 1;y1 <= n;y1++){for(int x2 = x1;x2 <= n;x2++){for(int y2 = y1;y2 <= n;y2++){k = pre[x2][y2] - pre[x1-1][y2] - pre[x2][y1-1] + pre[x1-1][y1-1];ans = max(ans,k);}}}}cout << ans << '\n';return 0;
}

小葱的01串 （固定区间大小的滑动窗口）

题目链接

题解

1. 环形的区域不需要统计，在字符串中间的区间如果是符合要求的，那么统计的次数加2，不在字符串中间的区间，那么统计次数加1
2. 统计区间为字符串长度的一半，如果这一半的0的个数和1的个数等于另一半0的个数和1的个数，那么就是符合要求的区间
3. 细节问题：right枚举到n-2位置就结束，因为再向后枚举就重复统计次数了，在第一个区间统计的时候就考虑了后面的区间了
4. 比如0101，如下图

代码

// 方法一
#include<iostream>
#include<string>
using namespace std;int main()
{int n;cin >> n;string s;cin >> s;int l = 0,y = 0;for(auto ch : s){if(ch == '0') l++;else y++;}int k = n / 2;// 滑动窗口的区间大小int left = 0,right = 0;int ans = 0;int ling = 0,yi = 0;while(right < n){// 进窗口if(s[right] == '0') ling++;else if(s[right] == '1') yi++;// 判断if(right - left + 1 == k){// 更新结果if(ling == l - ling && yi == y - yi && right != n-1 &&left != 0){ans += 2;}else if(ling == l - ling && yi == y - yi){ans++;}// 出窗口if(s[left] == '0') ling--;else yi--;left++;}right++;}cout << ans << '\n';return 0;
}// 方法二
#include<iostream>
#include<string>
using namespace std;int n;
string s;int main()
{cin >> n >> s;int count[2] = {0};// 统计所有0和1的个数for(auto ch : s){count[ch-'0']++;}int left = 0,right = 0,ret = 0,half = n / 2;// 统计窗口里0和1的个数int hash[2] = {0};// 最后一个再统计就重复统计了// 考虑第一个区间的时候,后面的区间实际上已经考虑过了while(right < n - 1){// 进窗口hash[s[right]-'0']++;// 出窗口while(right - left + 1 > half){hash[s[left++] - '0']--;}// 更新结果if(right - left + 1 == half){if(hash[0] * 2 == count[0] && hash[1] * 2 == count[1]){ret += 2;}}right++;}cout << ret << '\n';return 0;
}