数据结构实验7.2:二叉树的基本运算
文章目录
- 一,实验目的
- 二,问题描述
- 三,基本要求
- 四,实验操作
- 五,示例代码
- 六,运行效果
一,实验目的
- 深入理解树与二叉树的基本概念,包括节点、度、层次、深度等,清晰区分二叉树与一般树的结构特点,为后续学习和应用打下坚实基础。
- 熟练掌握用递归方法实现二叉树的遍历,通过递归算法的设计和实现,深刻体会递归思想在处理树结构数据时的简洁性和高效性,提高对递归算法的运用能力。
- 掌握借助栈或队列实现二叉树遍历的非递归迭代方法,理解栈和队列在模拟递归过程中的作用,培养利用数据结构解决问题的能力,拓宽算法设计思路。
- 熟练掌握构造Huffman树、Huffman编码等操作,理解Huffman树的原理和应用场景,能够根据给定的字符频率构建最优的Huffman树,并生成相应的Huffman编码,提高对数据压缩等实际问题的解决能力。
- 通过对二叉树相关知识的学习和编程实践,加深对二叉树的理解,逐步培养运用二叉树结构解决实际问题的编程能力,提升算法设计、调试和分析的综合素养。
二,问题描述
编程实现二叉树的下列基本运算。
(1)创建一棵二叉树;
(2)求二叉树中结点的总数;
(3)统计二叉树的叶结点个数;
(4)求二叉树的深度;
(5)用按层次顺序遍历二叉树的方法,统计树中具有度为1的结点数目;
(6)交换二叉树每个结点的左孩子和右孩子;
(7)输出二叉树。
三,基本要求
(1)采用二叉链表作为二叉树结点的存储结构;
(2)设计实现上述各种运算的算法;
(3)设计主函数以完成对上述算法的调用,并输出结果;
(4)完善参考程序;
(5)设计测试数据,上机调试、测试完善后的参考程序,保存并打印测试结果,对算法性能进行分析。
四,实验操作
1,双击Visual Studio程序快捷图标,启动程序。

2,之前创建过项目的话,直接打开即可,这里选择【创建新项目】。

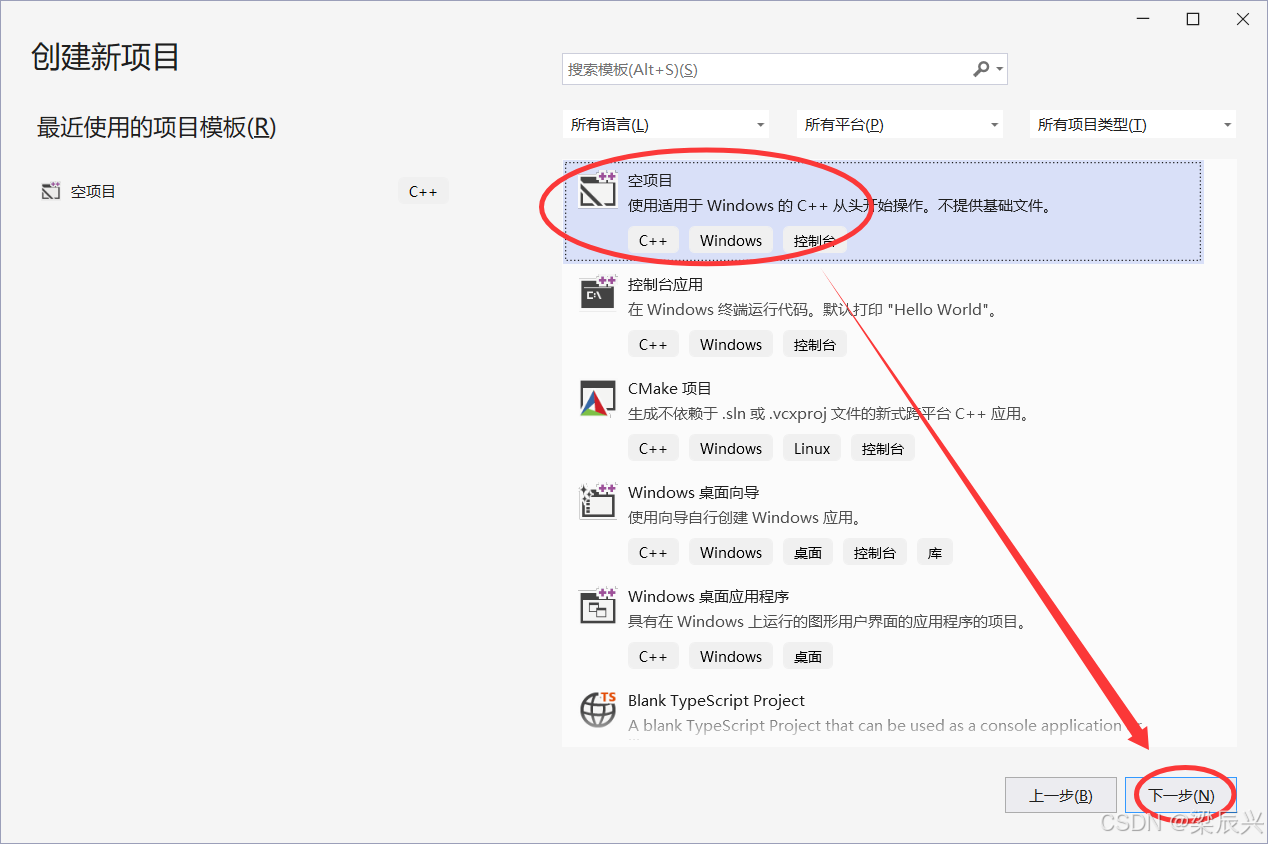
3,单击选择【空项目】——单击【下一步】按钮。
4,编辑好项目的名称和存放路径,然后单击【创建】按钮。

5,创建C++程序文件,右击【源文件】——选择【添加】——【新建项】。

6,输入项目名称,单击【添加】按钮。

7,编写代码,单击运行按钮,运行程序。

五,示例代码
#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>typedef struct BiTNode { // 定义二叉树的结点结构char data; // 假定树结点的元素类型为charstruct BiTNode* lchild; // 左指针struct BiTNode* rchild; // 右指针
} BiTNode, * BiTree;void CreateBiTree(BiTree& T)
{ // 先序递归遍历方式创建一棵二叉树char ch;scanf("\n%c", &ch); // 输入根结点的值if (ch == '#') // 终止项T = NULL;else{T = (BiTree)malloc(sizeof(BiTNode)); // 创建根结点if (!T)exit(-1);T->data = ch;printf("\n请输入%c结点的左子结点(#表无):", T->data); // 先序遍历创建左子树CreateBiTree(T->lchild);printf("\n请输入%c结点的右子结点(#表无):", T->data); // 先序遍历创建右子树CreateBiTree(T->rchild);}
}//统计二叉树的叶子结点个数。
int LeafNodeCount(BiTree T)
{if (T == NULL)return 0; //如果是空树,则叶子结点个数为0else if (T->lchild == NULL && T->rchild == NULL) // 判断该结点是否是叶子结点(左孩子右孩子都为空),若是则返回1return 1;elsereturn LeafNodeCount(T->lchild) + LeafNodeCount(T->rchild);
}//交换二叉树每个结点的左孩子和右孩子。
void ChangeLR(BiTree T)
{BiTree p;if (T == NULL || (T->lchild == NULL && T->rchild == NULL))return;else{p = T->lchild;T->lchild = T->rchild;T->rchild = p;}ChangeLR(T->lchild);ChangeLR(T->rchild); // 交换右子树上结点的左右孩子
}
// 统计二叉树中度为1的结点数
int D1_Nodes(BiTree T)
{int num1, num2;if (T == NULL || (!T->lchild && !T->rchild))return 0;num1 = D1_Nodes(T->lchild);num2 = D1_Nodes(T->rchild);if (T->lchild && !T->rchild) // 若结点T的左子树非空,右子树空,则返回左// 子树上度为1的结点数加1(当前结点度为1)return num1 + 1;else if (!T->lchild && T->rchild)return num2 + 1;elsereturn num1 + num2;
}//求二叉树结点数目
int Nodes(BiTree T)
{int num1, num2;if (T == NULL)return 0;else {num1 = Nodes(T->lchild); // 统计左子树的结点数num2 = Nodes(T->rchild); // 统计右子树的结点数return num1 + num2 + 1; // 左右子树结点总数加1(当前结点)}
}// 求二叉树的深度
int BiTreeDepth(BiTree T)
{int leftdep, rightdep;if (T == NULL) // 终止项return 0;else{leftdep = BiTreeDepth(T->lchild);rightdep = BiTreeDepth(T->rchild);return (leftdep > rightdep) ? (leftdep + 1) : (rightdep + 1);}
}
//以括号表示格式输出二叉树
void OutputBiTree(BiTree T)
{ // 先序递归遍历方式输出括号表示的二叉树if (T != NULL) // 终止项{printf("%c", T->data); // 访问根结点if (T->lchild != NULL || T->rchild != NULL){printf("("); // 根的孩子用圆括号对括OutputBiTree(T->lchild); // 先序遍历输出左子树if (T->rchild != NULL)printf(","); // 根的左右孩子以“,”分隔OutputBiTree(T->rchild); // 先序遍历输出右子树printf(")"); // 根的孩子用圆括号对括}}
}void main()
{int n;BiTNode* proot; // 定义树proot = NULL; // 初始化为空树printf("请输入根结点元素(#表无):"); // 创建二叉树CreateBiTree(proot);printf("\n(1)二叉树创建成功!其括号表示格式输出:\n\t");OutputBiTree(proot);printf("\n");n = Nodes(proot);printf("(2)二叉树结点总数是:%d\n", n);n = LeafNodeCount(proot);printf("(3)二叉树的叶子结点数为:%d\n", n);n = BiTreeDepth(proot);printf("(4)二叉树的深度是:%d\n", n);n = D1_Nodes(proot);printf("(5)二叉树中度为1的结点数是:%d\n", n);ChangeLR(proot);printf("(6)交换所有结点的左右孩子后二叉树括号表示法输出:\n\t");OutputBiTree(proot);printf("\n");
}
六,运行效果
1,实验测试效果。

2,编写代码运行后的效果。

