当前位置：首页 > news >正文

人工智能-机器学习其他技术(决策树，异常检测，主成分分析)

news 来源：原创 2025/4/21 6:33:22

决策树

一种对实例进行分类的树形结构，通过多层判断区分目标所属类别
本质：通过多层判断，从训练数据集中归纳出一组分类规则
优点：
计算量校，运算速度快
易于理解
缺点：
忽略属性间的相关性
样本分布不均时，影响模型表现
问题核心：特征选择，每个节点应该选用哪个特征

决策树求解

三种求解方法：
ID3, C4.5, CART
ID3:
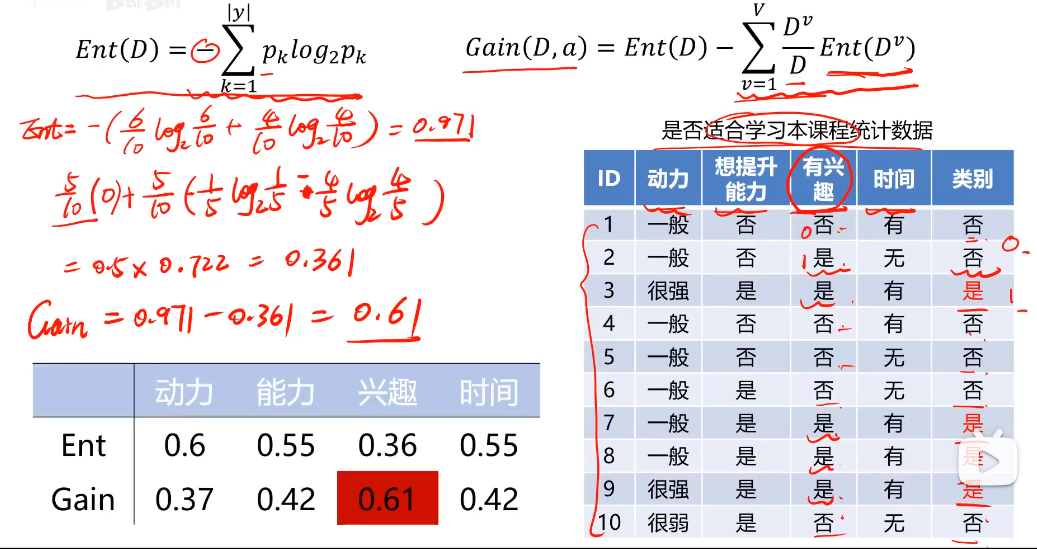
利用信息熵原理选择信息增益最大的属性作为分类属性，递归地拓展决策树的分支，完成决策树的构造。
信息熵(entropy)：度量随机变量不确定性的指标，熵越大，变量的不确定性越大。
在这里插入图片描述
注:
Pk=1，Ent(D)=0.
Pk=0, Ent(D)=0.

异常检测

根据输入数据，对不符合与预期模式的数据进行识别
核心：寻找低概率数据（事件）
在这里插入图片描述
概率密度：
描述随机变量在某个确定的取值点附近的可能性的函数

高斯分布说明西格玛越小，数据越集中。

主成分分析

数据降维

案例：通过美国192901938年各年经济数据，预测国民收入与支出。
数据包括：雇主补贴，消费资料，生产资料，公共支出，股息，利息等17个指标
通过主成分分析将17个指标降维成3个指标。
数据降维：是指在某些限定条件下，降低随机变量个数，得到一组“不相关”主变量的过程。
作用：
减少模型分析数据量，提升处理效率，降低计算难度；
实现数据可视化。

数据降维的实现：主成分分析（PCA）

PAC(principal components analysis):数据降维技术中，应用最多的方法
目标：寻找k(k<n)维新数据，使他们反映事物的主要特征
核心：在信息损失尽可能少的情况下，降低数据维度
3D到2D：
投影到u1,u2形成的平面
n维到k维：
投影到u1,u2…uk形成的空间
如何保留主要信息：投影后的不同特征数据尽可能分得开（即不相关）
如何实现？
使投影后的方差最大，因为方差越大数据也越分散
计算过程：
原始数据预处理（标准化：μ=0,σ=1)
计算协方差矩阵特征向量，及数据在各特征向量投影后的方差
根据需要（任务指定或方差比例）确定降维维度k
选取k维特征向量，计算数据在其形成空间的投影

实战

Iris数据集

Iris鸢尾花数据集是一个经典数据集，在统计学习和机器学习领域都经常被用作示例
3类共150条记录，每类各50个数据
每条记录都有4项特征：
花萼长度(Sepal Length)，花萼宽度，花瓣长度(Petal Length)，花瓣宽度
在这里插入图片描述

1.决策树实现iris数据分类

1、基于irsi_data.csv数据，建立决策树模型，评估模型表现；
2、可视化决策树结构
3、修改min_samples_leaf参数，对比模型结果

#load the data
import pandas as pd
import numpy as np
data = pd.read_csv('iris_data.csv')
data.head()

#define the X and y
X = data.drop(['target','label'],axis=1)
y = data.loc[:,'label']
print(X.shape, y.shape)

注: drop([‘target’,‘label’],axis=1)是去掉’target’,'label’这两列

#establish the decision tree model
from sklearn import tree
dc_tree = tree.DecisionTreeClassifier(criterion='entropy',min_samples_leaf=5)
dc_tree.fir(X, y)

注:min_samples_leaf表示在决策树的叶子节点（即最终的分类节点）中，每个叶子节点所包含的最小样本数量.偏差衡量模型对训练数据的拟合程度，方差衡量模型对新数据的泛化能力。较小的 min_samples_leaf 值会使模型更复杂，偏差更小，但方差更大；较大的 min_samples_leaf 值会使模型更简单，偏差更大，但方差更小。

#evaluate the model
y_predict = dc_tree.predict(X)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)

#visualize the tree
%matplotlib inline
from matplotlib import pyplot as plt
fig = plt.figure(figsize(20,10))
tree.plot_tree(dc_tree, filled='True',feature_names=['SepalLength','SepalWidth','PetaLength','PetalWidth'],class_names=['setosa','versicolor','virginica'])

决策树实战总结：
1、通过建立决策树，可实现对标签数据的有效分类
2、通过修改叶子节点最少样本数量对应参数min_samples_leaf，可调控树的分支深度

2.异常数据检测

1、基于anomaly_data.csv数据，可视化数据分布情况、及其对应高斯分布的概率密度函数
2、建立模型，实现异常数据点预测
3、可视化异常检测处理结果
4、修改概率分布阈值EllipticEnvelope(contamination=0.1)中的contamination,查看阈值改变对结果的影响

#load the data
import pandas as pd
import numpy as np
data = pd.read_csv('anomaly_data.csv')
data.head()

#visualize the data
%matplotlib inline
from matplotlib import pyplot as plt
fig1 = plt.figure(figsize(10,5))
plt.scatter(data.loc[:,'x1'],data.loc[:,'x2'])
plt.title('data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()

#define the x1 and x2
x1 = data.loc[:,'x1']
x2 = data.loc[:,'x2']

#visual the data
fig2 = plt.figure(figsize=(10,5))
plt.subplot(121)
plt.hist(x1, bins=100)
plt.title('x1 distribution')
plt.xlabel('x1')
plt.ylabel('counts')
plt.subplot(122)
plt.hist(x2, bins=100)
plt.title('x2 distribution')
plt.xlabel('x2')
plt.ylabel('counts')
plt.show()

#calculate the mean and sigma of x1 and x2
x1_mean = x1.mean()
x1_sigma = x1.std()
x2_mean = x2.mean()
x2_sigma = x2.std()
print(x1_mean,x1_sigma,x2_mean,x2_sigma)

#calculate the gaussion distribution p(x)
from scipy.stats import norm
x1_range = np.linspace(0,20,300)
x1_normal = norm.pdf(x1_range,x1_mean,x1_sigma)
x2_range = np.linspace(0,20,300)
x2_normal = norm.pdf(x2_range,x2_mean,x2_sigma)
#print(x1_range)
#print(x1_normal)

 #visual the p(x)fig2 = plt.figure(figsize=(10,5))plt.subplot(121)plt.plot(x1_range,x1_normal)plt.title('normal p(x1)')plt.subplot(122)plt.plot(x2_range,x2_normal)plt.title('normal p(x2)')plt.show()

#establish the model and predict
from sklearn.coariance import EllipticEnvelope
ad_model = EllipticEnvelope()
ad_model.fit(data)

#make prediction
y_predict = ad_model.predict(data)
#print(y_predict)
print(pd.value_counts(y_predict))

#visualize the result
fig4 = plt.figure(figsize=(10,5))
plt.scatter(data.loc[:,'x1'],data.loc[:,'x2'],maker='x')
plt.scatter(data.loc[:,'x1'][y_predict==-1],data.loc[:,'x2'][y_predict==-1],maker='o',facecolor='none',edgecolor='red',s=150)
plt.title('anomaly detection result')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend((original_data,anomaly_data),('original_data','anomaly_data'))
plt.show()

ad_model = EllipticEnvelope(contamination=0.02)
ad_model.fit(data)
y_predict = ad_model.predict(data)
#visualize the result
fig5 = plt.figure(figsize=(20,10))
plt.scatter(data.loc[:,'x1'],data.loc[:,'x2'],maker='x')
plt.scatter(data.loc[:,'x1'][y_predict==-1],data.loc[:,'x2'][y_predict==-1],maker='o',facecolor='none',edgecolor='red',s=150)
plt.title('anomaly detection result')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend((original_data,anomaly_data),('original_data','anomaly_data'))
plt.show()

PCA(iris数据降维后分类)

1、基于iris_data.csv数据，建立KNN模型实现数据分类(n_neighbors=3)
2、对数据进行标准化处理，选取一个维度可视化处理后的效果
3、进行与原数据等维度PCA，查看各主成分的方差比例
4、保留合适的主成分，可视化降维后的数据
5、基于降维后数据建立KNN模型，与原数据表现进行对比

#load data
import pandas as pd
import numpy as np
data = pd.read_csv('iris_data.csv')
data.head()

#defube X and y
X = data.drop(['target','label'],axis=1)
y = data.loc[:,'label']

#establish knn model and calculate the accuracy
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X,y)
y_predict = KNN.predict(X)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)

进行数据的标准化

from sklearn.preprocessing import StandardScaler
X_norm = StandardScaler().fit_transform(X)
print(X_norm)

#calculate the mean and sigma
x1_mean = X.loc[:,'sepal length'].mean()
x1_norm_mean = X_norm[:,0].mean()
x1_std = X.loc[:,'sepal length'].std()
x1_norm_std = X_norm[:,0].std()
print(x1_mean,x1_norm_mean,x1_std,x1_norm_std)

%matplotlib inline
from matplotlib import pyplot as plt
fig1 = plt.figure(figsize(20,5))
plt.subplot(121)
plt.hist(X.loc[:,'sepal length'],bins=100)
plt.subplot(122)
plt.hist(X_norm[:,0],bins=100)
plt.show()

print(X.shape)

#pca analysis
from sklearn.decomposition import PCA
pca = PCA(n_components=4)
X_pca = pca.fit_transform(X_norm)
#calculate the variance ratio of each principle components
var_ratio = pca.explained_variance_ratio_ #计算各个成分的方差
print(var_ratio)

fig2 = plt.figure(figsize=(20,5))
plt.bar([1,2,3,4],var_ratio)
plt.xticks()
plt.ylabel('variance ratio of each PC')
plt.show()

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_norm)
print(X_pca.shape)

#visualize the PCA result
fig3 = plt.figure(figsize=(10,10))
setosa=plt.scatter(X_pca[:,0][y==0],X_pca[:,1][y==0])
versicolor=plt.scatter(X_pca[:,0][y==1],X_pca[:,1][y==1])
virginica=plt.scatter(X_pca[:,0][y==2],X_pca[:,1][y==2])
plt.legend((setosa,versicolor,virginica),('setosa','versicolor','virginica'))
plt.show()

KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X_pca,y)
y_predict = KNN.predict(X_pca)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)