【计量地理学】实验七 多种地统计方法的插值比较

一、实验目的

1. 熟悉并掌握常见的空间插值方法：通过实际操作，了解普通克里格法、回归克里格法、反距离加权法和全局多项式回归等常用的空间插值方法；
2. 探究不同插值方法的原理与适用场景：通过实际操作深入理解每种插值方法的工作原理、结果精度以及适用范围，以便在实际问题中选择合适的方法；
3. 比较不同插值方法的预测精度：通过对比各插值方法生成的预测结果，分析它们的相关系数、平均误差和均方根误差等指标，评价其预测精度；
4. 分析空间波动性：重点学习理解并计算空间波动性指标，并学会利用空间波动性指标比较不同插值方法生成的预测结果在空间上的变化程度，从而更深入了解各方法的原理以及其对于空间波动性的反映能力。

 二、实验内容

1. 数据处理
2. 普通克里格法
3. 回归克里格法
4. 反距离加权法
5. 全局多项式回归

 三、实验过程

（一）数据处理

首先利用ArcGIS中的子集提取工具，将数据集分为训练集与检验集：

（二）普通克里格法

1.插值结果：

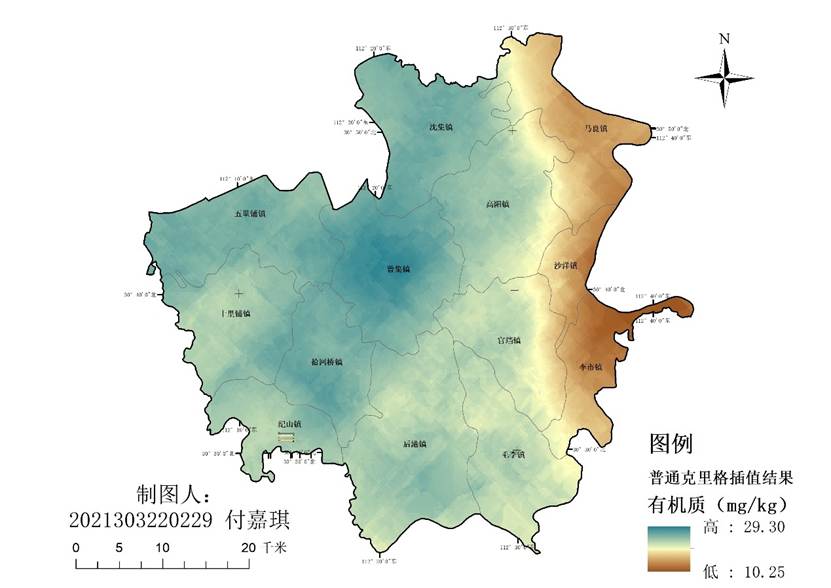
图 1 普通克里格插值结果图

2.精度检验：

我们利用MATLAB软件中的相关函数对插值结果进行精度评价，评价指标包括相关系数，平均误差和均方根误差，详细代码如下所示：

而对插值结果的定量化空间波动性评价，我选择利用的是ArcGIS软件中的【焦点统计】，谈及数据的波动性评价，方差与标准差即非常典型的数据波动性指标，但这类指标往往只适用于属性数据，难以体现我们空间数据的波动性。

但处于此根本原理，我想到可以利用ArcGIS中的【焦点统计】工具，该工具可以帮助我们计算得到栅格图像中每个像素与其邻域范围内的标准差，在得到的图像结果中直接查看计算的标准差的平均值，即可作为我们一幅栅格图像的定量化空间波动性指标：

最终得到结果如下表格所示，后续插值方法中不再赘述预测结果图与精度检验结果表格的获得方法：

表1普通克里格精度检验结果

相关系数	平均误差	均方根误差	值域范围	空间波动性
0.69134	-0.011632	3.6687	16.359	0.163

（三）回归克里格法

1.插值结果：

首先利用SPSS软件对有机质与13个环境变量进行回归分析，得到公式后在ArcGIS中计算得到回归结果，将数据利用【多值提取至点】与【表转Excel】工具将回归结果导入至Excel，并计算得到残差，再将残差数据连接至ArcGIS中：

随后在ArcGIS中对残差数据进行普通克里格插值，将残差的克里格插值结果与我们之前所得的回归结果利用【栅格计算器】工具相加，即可得到插值结果：

图 2 回归克里格插值结果图

2.精度检验：

表2回归克里格精度检验结果

相关系数	平均误差	均方根误差	值域范围	空间波动性
0.7701	-0.077655	3.414	24.467	1.336

（四）反距离加权法

1.插值结果：

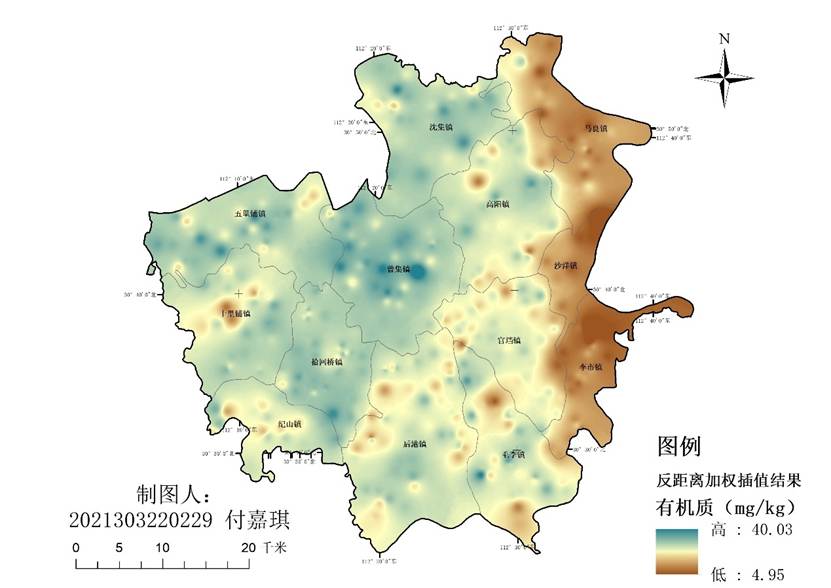
图 3 反距离加权插值结果图

2.精度检验：

表3反距离加权精度检验结果

相关系数	平均误差	均方根误差	值域范围	空间波动性
0.63804	0.04531	4.015	17.485	0.276

0.63804

0.04531

4.015

17.485

0.276

（五）全局多项式回归

1.插值结果：

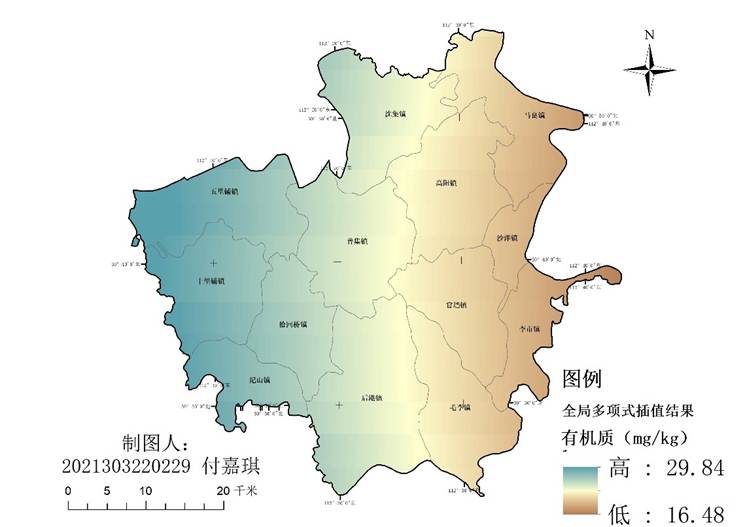
图 4 全局多项式插值结果图

2.精度检验：

表4全局多项式精度检验结果

相关系数	平均误差	均方根误差	值域范围	空间波动性
0.51536	0.26034	4.3462	10.492	0.035

四、实验结果分析

表5多种插值方法结果精度比较

	相关系数	平均误差	均方根误差	值域范围	空间波动性
普通克里格	0.69134	-0.0116	3.6687	16.359	0.163
回归克里格	0.7701	-0.0776	3.414	24.467	1.336
反距离加权	0.63804	0.04531	4.015	17.485	0.276
全局多项式回归	0.51536	0.26034	4.3462	10.492	0.035

1. 总体空间趋势：通过比较四种插值方法结果图可以看出，四种不同插值方法得到有机质的预测结果在空间分布趋势上具有一致性，都呈现出西高东低的空间分布趋势，因此我们可以初步粗略地判断我们的插值方法与结果在大体方向上没有错误；
2. 插值结果精度：通过观察表5可得，回归克里格法的相关系数最大，均方根误差最小，全局多项式回归法的相关系数最小，均方根误差最大，这也在一定程度上对应符合了我们各个插值方法的原理，回归克里格法结合了环境变量的回归分析结果，能够更准确地预测有机质的空间分布，得到更好的预测结果，而全局多项式回归法因为假设数据间的关系是全局的，当数据的空间特征较为复杂或非线性时，可能无法捕捉到数据的细节趋势，因此预测精度较低，最终我们得到结果，插值结果精度从高到低为：回归克里格法、普通克里格法、反距离加权法、全局多项式回归法；
3. 空间波动性：空间波动性衡量的是空间数据在空间范围内的变化程度，较高的空间波动性意味着数据在连续空间上变化较大。通过观察表5可得，回归克里格法的空间波动性最高，为1.336，其次是反距离加权法为0.276，普通克里格法和全局多项式回归法的空间波动性较低，分别为0.163和0.035，空间波动性在我们得到的四幅结果图中也有体现，回归克里格法得到的结果图最为“破碎”，全局多项式回归法得到的结果最为“平滑”，对应了它们的空间波动性，这也与我们上述所谈到的它们的插值原理相符。

五、实验心得与不足

本次实验中，我们重点学习并结合具体数据利用普通克里格法、回归克里格法、反距离加权法以及全局多项式回归法等四种常见的空间插值方法进行数据预测，并通过对比不同方法的插值结果及其精度评价，深入了解学习了各个插值方法的基本原理、适用范围以及结果精度，其中重点学习与了解了定量化空间波动性这一概念并尝试进行了相关的计算。

但本次实验依然存在一些不足之处，例如在进行插值处理时未对异常值进行详细处理与分析，因此存在插值结果精度未能达到较好效果的情况，除此之外，对于空间波动性的相关计算：我采用的是利用【焦点统计】工具计算每个像素与周围8个像素的标准差，最后取研究区域内的平均值作为定量化的空间波动性指标，为达到更好的效果，本还可以对该数据进行平方标准化等处理使其更为规范，但由于时间与能力限制并未进行优化，有待后续的学习与完善。