数据结构第六章（五）-拓扑排序、关键路径

---

图的应用（二）

---

一、有向无环图

首先我们得知道什么是有向无环图，它其实就是字面意思，一个有向没环的图。

有向无环图：若一个有向图中不存在环，则成为有向无环图，简称DAG图（DAG，Directed Acyclic Graph）。

没环的不就是树吗，我感觉这就是个有向树。

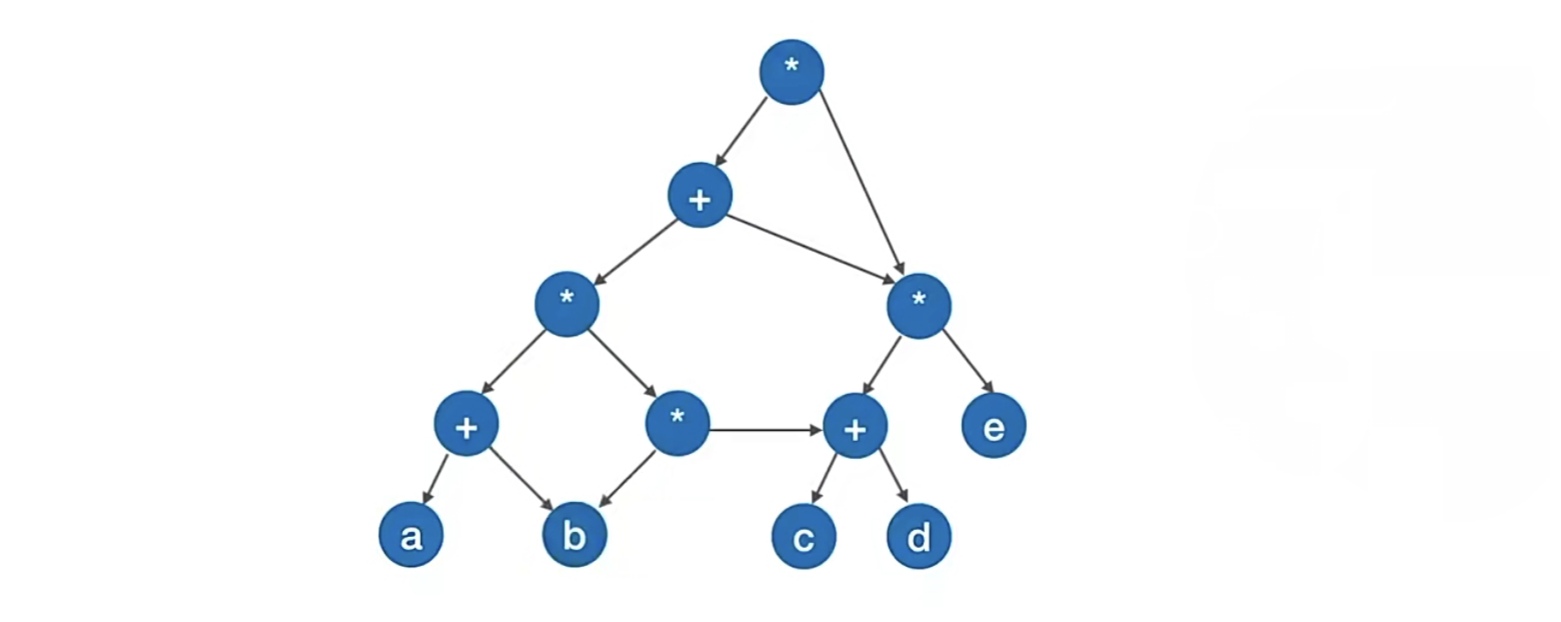
来看下面的一个DAG图：

最上面的中缀表达式显然就是先根遍历这个树。那么看这个树能发现什么？发现其实有很多重复的是不，比如下面深蓝色和绿色部分，长得一毛一样：

所以可以把它俩合并，这样可以省很多空间。但是合并后发现还有可以合并的，比如下面的绿色和红色部分：

所以再次合并。合并完之后我们发现没有能合并的了，这就是我们刚刚那个表达式的终极缩减形态：

有个真题就是这么出的(2019年)，它问你用有向无环图描述表达式 ((x+y)(x+y)/x) ，需要的顶点个数至少是多少个，额。先来画这个图：

然后我们找可以合并的地方，发现左下角那一小坨可以合并，合并后两个x也可以合并，最终形态就是这样：

所以需要5个顶点。

但是！！！我们又怎么知道到底需要多少个顶点？万一找错了找漏了又怎么办？所以我们需要一些步骤，按步骤来就能确保不会找错了：

步骤如下：

1. 把各个操作数不重复地排成一排；
2. 标出各个运算符的生效顺序（先后顺序有点出入无所谓）
3. 按顺序加入运算符，注意“分层”

分层是怎么分的？就是看这个运算要不要基于下面一层运算的结果来进行，要的话就在上一层。

比如下面这个表达式，我们发现操作数只有a,b,c,d,e，排成一排，再标出运算符生效顺序如下：

然后再根据上面的步骤分层加入运算符：

接着我们再看每一层有没有可以合并的运算符，记住，只看当前层，从下往上一层一层合并，不可以跨层！

我们发现要合并的其实只有从下往上数的第二层和第三层，这两层分别每层合并如下：

这就是我们刚刚那个表达式的终极形态。

二、拓扑排序

1. AOV网

AOV网（Activity On Vertex Network），其实是用顶点表示活动的网。

用DAG图（有向无环图）表示一个工程，顶点表示活动，有向边<v_i，v_j>表示活动v_i必须先于活动v_j进行。

其实就是一个有向图，必须得按箭头走，不能跨箭头先走后面的，除了这个就没啥了，下面我们讲拓扑排序：

2. 拓扑排序

所谓拓扑排序，就是找到做事的先后顺序。

比如下面这个图，你怎么找到这个图的做事的先后顺序？

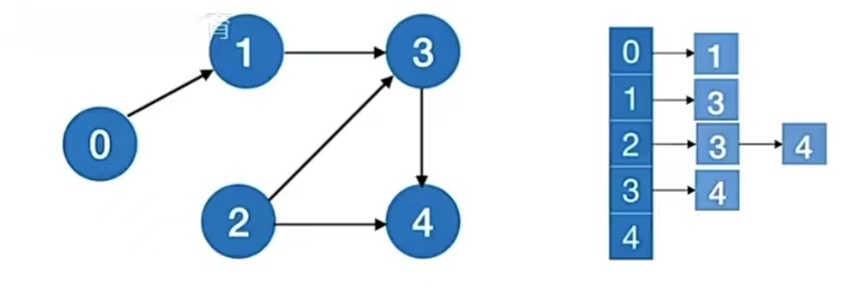
按照肉眼看，肯定是知道首先0和2是没有限制的，可以直接做；但是1和3和4不一样，1只有等0做完了才能做（因为它有一条来自0的入边），3只有等1和2做完了才能做（因为它有两条入边，一条来自1，一条来自2），4只有等2和3做完了才能做（同理，它有一条来自1的入边，有一条来自3的入边）。

所以我们的拓扑排序关键点就在于不能有错误的顺序（当然一个图的拓扑排序不止一个，只要是对的就可以）

那么什么是拓扑排序呢？

拓扑排序：在图论中，由一个有向无环图的顶点组成的序列，当且仅当满足下列条件时，称为该图一个拓扑排序：

• 每个顶点出现且只出现一次；
• 若顶点A在序列中排在顶点B的前面，则在途中不存在从顶点B到顶点A的路径。

或定义为：拓扑排序是对有向无环图的顶点的一种排序，它使得若存在一条从顶点A到顶点B的路径，则在排序中顶点B出现在顶点A的后面。每个AOV网都有一个或多个拓扑排序序列。

注意！！是对顶点进行排序哈。

又回到我们一开始说的，现在我们更加理解了“拓扑排序就是找做事的先后顺序”这一点，那我们接下来就要准备用代码实现了。

首先当然是考虑步骤，找没有入边的顶点，输出后再删除顶点和它的出边，完了再循环找没有入边的顶点……用队列或者栈都ok的

拓扑排序的实现：

1. 从AOV网中选择一个没有前驱（入度为0）的顶点并输出；
2. 从网中删除该顶点和所有以它为起点的有向边；
3. 重复1和2直到当前的AOV网为空或当前网中不存在无前驱的顶点为止。

看这个第3条，重复1和2直到当前的AOV网为空就可以了，为什么还要当前网中不存在无前驱的顶点？因为如果图中存在，说明既有顶点，我们又找不到没有入边的顶点，那就说明有回路，就是有环，查找拓扑排序序列失败。

看看代码更加清晰：

#define MaxVertexNum 10  //顶点数目的最大值//“边/弧”
typedef struct ArcNode{int adjvex;     //边/弧指向哪个结点struct ArcNode *next;  //指向下一条弧的指针int weight;     //边权值
}ArcNode;//“顶点” 
typedef struct VNode{char data;      //顶点信息，类型自定义ArcNode *first; //第一条边/弧
}VNode, AdjList[MaxVertexNum];//用邻接表存储的图
typedef struct{AdjList verticles;int vexNum, arcNum; //图的当前顶点数和边数/弧数
}Graph;//拓扑排序的实现
bool TopologicalSort(Grapic G){InitialStack(S);    //初始化栈，存储入度为0的顶点for(int i = 0; i < G.vexNum; i++){if(indegree[i] == 0){Push(s, i);     //将所有入度为0的顶点进栈}}int count = 0;      //计数，记录当前已经输出的顶点数while(!IsEmpty(S)){ //栈不空，则存在入度为0的顶点Pop(S, i);      //栈顶元素出栈print[count++] = i;   //输出顶点ifor(p = G.vericles[i].firstarc; p; p=p->nextarc){//将所有i指向的顶点入度-1，并且将入度减为0的顶点压入栈Sv = p->adjvex;if(!(--indegree[v])){Push(S, v); //入度为0，则入栈}}}//whileif(count < G.vexnum){return false;   //排序失败，有向图中有回路}else{return true;    //拓扑排序成功}
}

当然里面出现了 indegree数组、print数组，这两个数组一个记录当前顶点的入度，一个记录拓扑序列：

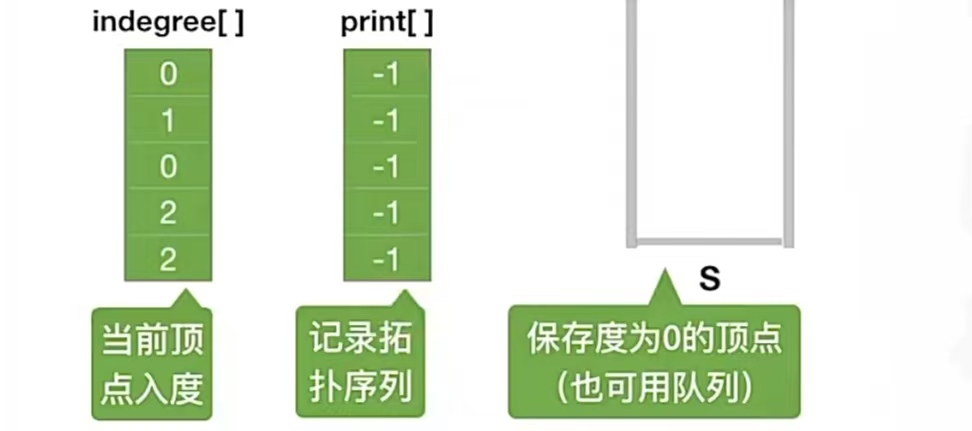
当前顶点的入度数组就是初始入度，拓扑序列数组初始都是 -1。

现在我们已经知道了拓扑排序的代码实现，那么随之而来的还是要分析一下它的时间复杂度和空间复杂度。根据上面的代码我们知道，主要时间消耗是在顶点出入栈和找顶点的邻接边，所以如果是按照上述邻接表存储图的话时间复杂度就是O(|V|+|E|)。

如果采用邻接矩阵，那显然时间复杂度就是O(|V|²)。

3. 逆拓扑排序

它就和它的名字一样，逆拓扑排序就是逆着的拓扑排序，也就是倒过来的拓扑排序。

所以就是找入度变成找出度，再删除这个点和它的入边，倒过来就行了。

对一个AOV网，如果采用下列步骤进行排序，则称之为逆拓扑排序：

1. 从AOV网中选择一个没有后继（出度为0）的顶点并输出；
2. 从网中删除该顶点和所有以它为终点的有向边；
3. 重复1和2直到当前的AOV网为空。

当然这个逆拓扑排序，如果还是用之前的邻接表存储的话找入边会非常麻烦。所以我们可以换存储的结构，就是换一个“逆邻接表”，之前不是存各个节点的下一个顶点吗，现在存各个结点的上一个顶点，就会容易许多。

我们用深度优先（DFS）实现：

void DFSTraverse(Graphic G){        //对图G进行深度优先遍历for(int i = 0; i < G.vexNum; i++){visited[v] = FALSE;          //初始化已访问标记数据}for(int i = 0; i < G.vexNum; i++){ //从0号结点开始遍历if(!visited[i]){            DFS(G,i);               //vi未访问过，从vi开始DFS}}
}//深度优先遍历
void DFS(Graphic G, int V){ //从顶点v出发，深度优先遍历图G// visit(v);           //访问初始顶点vvisited[v] = TRUE;  //对v做已访问标记for(w = FirstNeighbor(G,v) ; w >= 0; w = NextNeighbor(G,v,w)){//检测v所有的邻接点if(!visited[w]){    //w为v的尚未访问的邻接顶点DFS(G,w);}//if}//forprintf("%d",v); //输出顶点//注意：DFS实现逆拓扑排序，在顶点退栈前输出
}

为什么深度优先可以用来求逆拓扑序列呢？还记得吗，我们的深度优先其实是栈进行递归求的。什么时候开始弹出栈顶元素？那就是无法再往下递的时候，也就是没有下一个顶点的时候。但是！！！恰恰是这个时候，代表我们找到了可以输出的逆拓扑序列的顶点（因为逆拓扑序列没有出边就输出），所以逆拓扑序列可以用深度优先搜索（DFS）求。

DFS实现逆拓扑排序，在顶点退栈前输出。

小总结一下：拓扑排序可以计算一个图中有没有环。 拓扑排序、逆拓扑排序序列可能不唯一；如果图中有环，则不存在拓扑排序序列/逆拓扑排序序列。

三、关键路径

1.AOE网

在带权有向图中，以顶点表示事件，以有向边表示活动，以边上的权值表示完成该活动的开销（如完成活动所需的时间），称之为用边表示活动的网络，简称AOE网（Activity On Edge NetWork）

下面是一个水灵灵的AOE网：

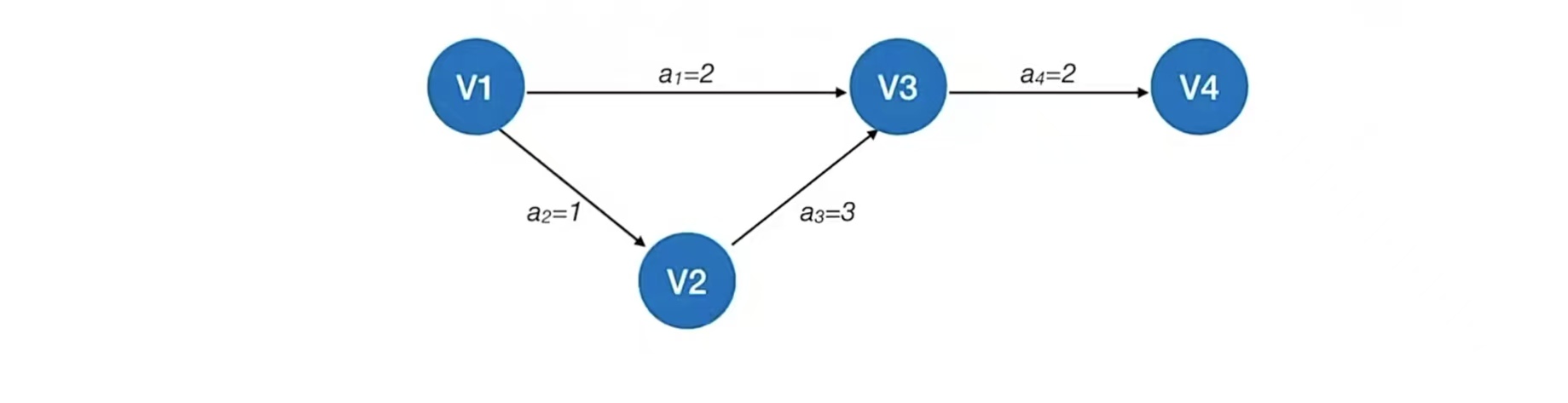
但是“事件”和“活动”仍然觉得很抽象，所以应该怎么理解呢？大概就是我们写完代码提交git，写代码是一个过程，提交是一个动作，那么写代码就是一个活动，commit and push就是一个事件，这么想就可以了。写代码不理解也没关系，也可以理解为是一个小学生，每次都需要举手才能回答问题，回答完问题就放下手，举手、放下就是事件，回答问题就是活动，这样也方便我们理解为什么要区分顶点和活动以及什么是AOE网。

AOE网具有以下两个性质：

1. 只有当某顶点所代表的事件发生后，从该顶点出发的各有向边所代表的活动才能开始；
2. 只有在进入某顶点的各有向边所代表的活动都已经结束时，该顶点所代表的事件才能发生。

另外，有些活动是可以并行进行的。

什么意思呢？就看我们上面那个图，只有v₁ 代表的事件发生后，a₁ 和a₂ 代表的活动才能开始；只有当a₃ 和a₃ 代表的活动都已经结束时，v₃ 顶点代表的时间才能发生

a₁ 活动和a₂ 活动是可以并行进行的，它们没有先后顺序。

在AOE网中仅有一个入度为0的顶点，称为开始顶点（源点），它标示整个工程的开始；
也仅有一个出度为0的顶点，称为结束顶点（汇点），它表示整个工程的结束。

2.关键路径

2.1 介绍

从源点到汇点的有向路径可能有多条，所有路径中，具有最大路径长度的路径称为关键路径，而把关键路径上的活动称为关键活动。

比如上面这个图，从源点到汇点的有向路径有多条，v₁——>v₃——>v₄，还有v₁——>v₂——>v₃——>v₄，这两条中最大的是v₁——>v₂——>v₃——>v₄，它的路径长度是6，是最大长度的路径，所以这条路上的就是关键路径，这条关键路径上的活动a₁、a₃、a₄就是关键活动。

完成整个工程的最短时间就是关键路径的长度，若关键活动不能按时完成，则整个工程的完成时间就会延长。

因为你要想完成整个工程，那就得每个活动都完成，所以最长的那条也得完成，它就是你需要完成这个工程的时间，它影响了你的工程的工期。

事件 v_k 的最早发生时间 ve(k) ——决定了所有从 v_k 开始的活动能够开工的最早时间
活动 a_k 的最早发生时间 e(k) ——指该活动弧的起点所表示的事件的最早发生时间

比如上面那个图，v₁的最早发生时间就是0，因为它前面没有指向它的需要发生的东西，v₂的最早发生时间是1，v₃的最早发生时间是2。v₃的最早发生时间，一个是要a₂执行完，一个是要a₃执行完，所以v₃的最早发生时间就是4，那么v₄的最早发生时间就是6

活动a₁的最早发生时间是0，a₂的最早发生时间是0，a₃的最早发生时间是1，a₄的最早发生时间是4。

事件 v_k 的最迟发生时间 vl(k) ——它是指在不推迟整个工程完成的前提下，该事件最迟必须发生的时间
活动 a_k 的最迟发生时间 l(k) ——它是指该活动弧的终点所表示事件的最迟发生时间与该活动所需时间之差

再比如上面那个图，如果我们要在6这个时间完成这个工程，那么从后往前推，v₃的最迟发生时间就是4，v₂的最迟发生时间就是1，v₁的最迟发生时间就是0。

活动a₄的最迟发生时间是4，a₁的最迟发生时间是2，a₃的最迟发生时间是1，a₂的最迟发生时间是0。

那么一个活动的最早发生时间和最迟发生时间，在关键路径上是一样的，在非关键路径上可能不一样，所以会有个概念叫活动a_i的时间余量d(i)=l(i)-e(i)，表示在不增加完成整个工程所需总时间的情况下，活动a(i)可以拖延的时间

若一个活动的时间余量为0，则说明该活动必须要如期完成，d(i)=0即l(i)=e(i)的活动a_i是关键活动

比如我们上面的那个图中，a₂，a₃，a₄就是关键活动。a₁不是关键活动，a₁从时间0或者时间2开始都可以，都不会影响工期。

2.2 关键路径的求法

求关键路径的步骤如下：

1. 求所有事件的最早发生时间 ve（）
2. 求所有事件的最迟发生时间 vl（）
3. 求所有活动的最早发生时间 e（）
4. 求所有活动的最迟发生时间 l（）
5. 求所有活动的时间余量 d（）

d(i)=0 的活动就是关键活动，由关键活动可得关键路径

比如下面这个AOE网：

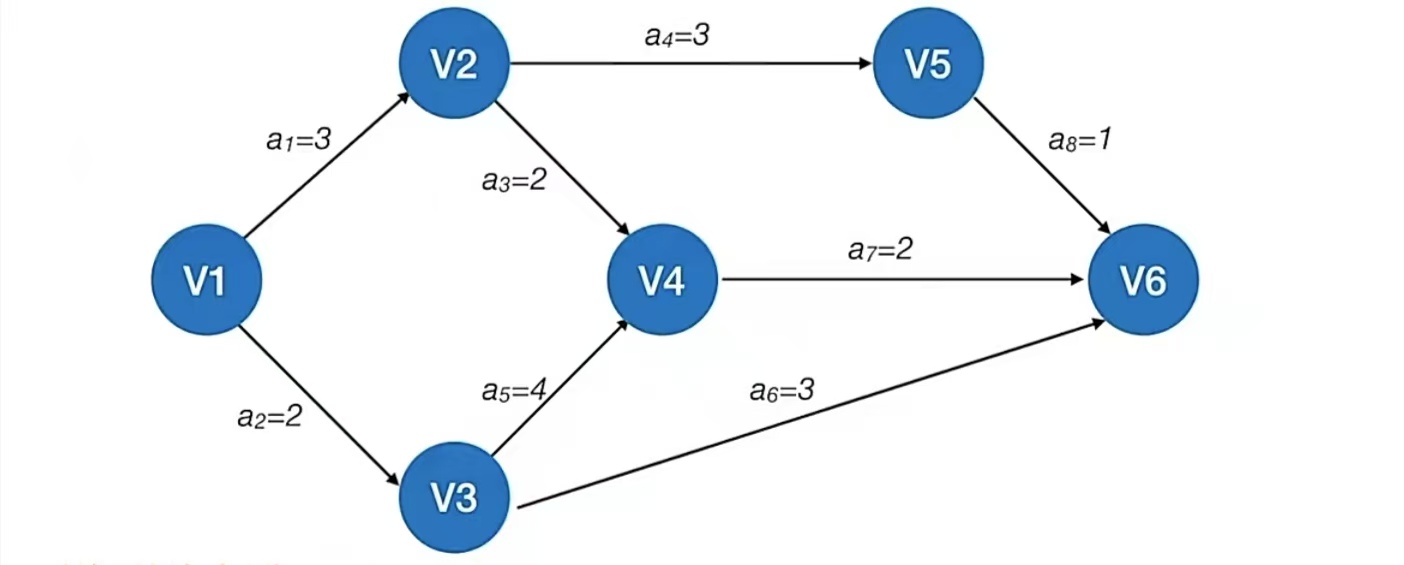
按照上述步骤求关键路径：

① 求所有事件的最早发生时间 ve（）

按照拓扑排序序列，依次求各个顶点的ve(k)：
ve(源点)=0
ve(k) = Max{ve(j) + Weight(v_j，v_k)}，v_j为v_k的任意前驱

拓扑序列： v₁， v₃， v₂， v₅， v₄， v₆
ve(1) = 0
ve(3) = 2
ve(2) = 3
ve(5) = 6
ve(4) = max{ ve(2) + 2 ，ve(3) + 4 } = 6
ve(6) = max{ ve(5) + 1 ，ve(4) + 2 ，ve(3) + 3 } = 8

	v1	v2	v3	v4	v5	v6
ve(k)	0	3	2	6	6	8

② 求所有事件的最早发生时间 vl（）

按照逆拓扑排序序列，依次求各个顶点的vl(k)：
vl(汇点)=ve(汇点)
vl(k) = Min{vl(j) + Weight(v_k，v_j)}，v_j为v_k的任意后继

逆拓扑序列： v₆， v₅， v₄， v₂， v₃， v₁
ve(6) = 8
ve(5) = 7
ve(4) = 6
ve(2) = min{ vl(5) - 1 ，vl(4) - 2 } = 4
ve(3) = min{ vl(4) - 4 ，vl(6) - 3 } = 2
ve(1) = 0

	v1	v2	v3	v4	v5	v6
ve(k)	0	3	2	6	6	8
vl(k)	0	4	2	6	7	8

③ 求所有活动的最早发生时间 e（）
若边<v_i ， v_j > 表示活动a_i ，则有 e(i) = ve(k)

意思就是，活动（边）的最早发生时间就是它的顶端的最发生时间。

所以：

	a1	a2	a3	a4	a5	a6	a7	a8
e(k)	0	0	3	3	2	2	6	6

④求所有活动的最迟发生时间 l（）
若边<v_i ， v_j > 表示活动a_i ，则有 l(i) = vl(k) - weight(v_k，v_j )

意思就是，活动（边）的最早发生时间就是它的顶端的最发生时间。

所以：

	a1	a2	a3	a4	a5	a6	a7	a8
e(k)	0	0	3	3	2	2	6	6
l(k)	1	0	4	4	2	5	6	7

⑤求所有活动的时间余量 d（）

d(i)=0 的活动就是关键活动，由关键活动可得关键路径

	a1	a2	a3	a4	a5	a6	a7	a8
e(k)	0	0	3	3	2	2	6	6
l(k)	1	0	4	4	2	5	6	7
d(k)	1	0	1	1	0	3	0	1

关键活动：a₂，a₅，a₇

关键路径： v₁，v₃，v₄，v₆

*关键路径的特性：（这个我们之前也说过）

• 若关键活动耗时增加，则整个工程的工期将增长；
• 缩短关键活动的时间，可以缩短整个工程的工期；
• 当缩短到一定程度时，关键活动可能会变成非关键活动

可能有多条关键路径，只提高一条关键路径上的关键活动速度并不能缩短整个工程的工期，只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。

---

总结

讲了拓扑排序和关键路径，主要就是关键路径的怎么求以及关键路径的性质，主要是得细心，不要算错就可以了。