BSTREE(二叉搜索树)的介绍与模拟实现
二叉搜索树的介绍
1.概念介绍
当学完了vector和list等容器和封装继承多态等特性后,接下来学习的就是BS树了,它的特性是:
1.所有的左子树小于根结点的值。
2.所有的右子树大于根结点的值。
3.它的左右子树也为二叉搜索树。
2.性能分析
当它接近满二叉树时,它的性能接近log2N,这得益于它的结构,由于它的左子树小于根节点,右子树大于根节点,每次比较就干掉一半的值,效率非常高。

相反当它的结构到达极端情况时,搜索效率会降低到O(n),退化成链表的结构。

3.二叉搜索树的插入
1.树为空,直接赋值给_root节点
2.树不为空,按照二叉搜索树的性质来,比根节点大,再去和右子树比较,比根节点小,再去和左子树比较,直到找到空位置。
注意:这个特性表示了它的插入顺序很可能影响搜索效率,比如在下面的二叉树中,如果我一开始就插入100这样的大值,那么根结点的右边就会不再插入值,会去左节点插入。

4.二叉树的查找
二叉树的查找是根据特性,当要查找的值比根节点大,向右子树走,比根节点小,向左子树走,直到找到与要查找的值相等的节点。
5.二叉树的删除
二叉树的删除我们分成几种情况来讨论:
1.要删除的节点左右子树都为空,由于左右子树都为空,所以删除它不影响其它节点,所以直接删除它即可。
2.删除的节点左子树为空但右子树不为空,这个时候把它的左子树托付给它的父节点即可,这时需要注意是向父节点的哪边插入。
3.删除的节点右子树为空但左子树不为空,这个时候和上述类似,思路就是把它的子节点托付给它的父节点,注意插入的方向即可。
4.删除的节点左右子树均不为空,这个时候我们要去查找该节点的右子树的最小值或者左子树的最大值来替代这个节点。这是由于二叉搜索树的特性导致的,该节点的右子树的所以节点大于该节点,这时需要找一个大于该节点的所以值中找一个最小的值,保证它比左子树的所有值大,比右子树的所有值小。类似的,左子树的所以节点的值都小于该节点,这时就需要在左子树中找一个最大的值来替代它,保证该值比左子树的所以值大,比右子树的所以值小。
当然,也可以这么说,找到它们左右子树中最特殊的来替代它就可以了。

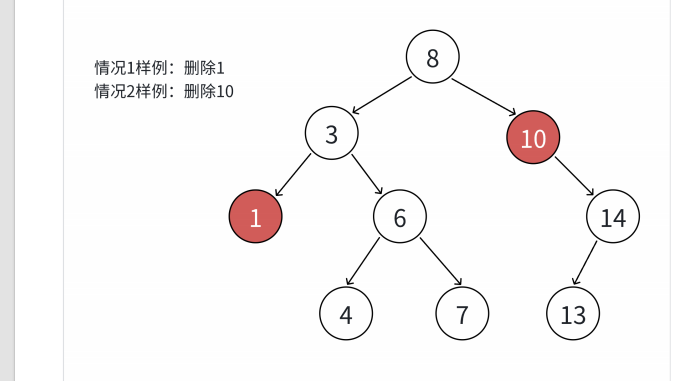
这里可以结合图片来理解一下:


2.二叉搜索树的模拟实现
接下来进入到我们的模拟实现环节,通过模拟实现二叉搜索树我们可以更好的理解它的特性,我们通过前面的知识了解到,当它的结构趋近于满二叉树时,它的搜索效率是非常高的,一下干掉一半的值,每进入到下一个节点时就会让数减半,试想,一亿个数按近似于满二叉树存入,我们每次进入下一个节点时就干掉一半的值,举个例子,一亿个数查找一个数,每次进入下一个节点时我们直接就令查找的数目减半。大大提高我们的搜索效率!!!
1.创建节点
二叉搜索树的数据是存储在节点中的,我们先实现一个节点。这里使用了类模板来实现了泛型编程,可以传int,string等。
template<class T>
struct node
{node(const T& data ){_left = _right = nullptr;_val = data;}node<T>* _left;node<T>* _right;T _val = 0;
};2.构造函数
构造函数我们不写,因为下面的私有变量中我们给了nullptr的缺省值,直接按缺省值进行初始化。
BSTREE()
{}3.二叉搜索树的成员变量
我们给一个跟节点即可,因为我们根节点存储的地址可以让操作者访问所有的二叉搜索树。
private:node<T>* _root = nullptr;4.插入操作
插入操作在上面介绍过了,在这里再简单说一下,根节点为空,直接new一个节点赋值给根节点,不为空根据二叉搜索树的特性,要插入的值比根节点小,向左走,大向右走,直到找到空位置进行插入。
bool Insert(const T& key)
{if (_root == nullptr){auto root = new node<T>(key);_root = root;return true;}node<T>* parent = _root;node<T>* cur = _root;while (cur != nullptr){if (cur->_val > key){parent = cur;cur = cur->_left;}else if (cur->_val < key){parent = cur;cur = cur->_right;}else{return false;}}/*cur->_val = key;*///理解一下这里为什么不对。。。原因是cur是空指针,对空指针赋值我简直太聪明了cur = new node<T>(key);if (parent->_val > key){parent->_left = cur;}else{parent->_right = cur;}return true;
}5.查找操作
查找的操作和插入的操作有异曲同工之妙,只不过把插入的目的变成了判断相等。
比跟节点大,向右走,小,向左走,相等返回,若找到nullptr还未找到要查找的值返回false表示未找到。
node<T>* Find(const T& key){if (_root==nullptr){return nullptr;}else{auto cur = _root;while (cur!=nullptr){if (cur->_val > key){cur = cur->_left;}else if (cur->_val < key){cur = cur->_right;}else{return cur;}}}return nullptr;}6.中序遍历
由于外部无法访问二叉搜索树的根节点,所以遍历我们写成私有,类的内部可以访问私有值,让接口来调用这个私有即可。
接下来介绍写法的重点:递归
核心思想是把一个问题分成若干个小问题,当满足某个条件时返回作为终止条件。
中序遍历是左根右,假如我们先简化,先访问左节点的值,然后打印,再去访问右节点的值,打印。终止条件为传的地址为nullptr。然后再推广,当它们的节点还有很多时,人脑是无法很快反应过来的,我们要从总体去看一下,就是将问题分解为相似的子问题,依赖终止条件回溯结果。

void InOrder()
{_InOrder(_root);cout << endl;
}
private:
void _InOrder(node<T>* root)//中序遍历
{if (root==nullptr){return ;}_InOrder(root->_left);cout << root->_val<<" ";_InOrder(root->_right);
}7.删除节点
删除节点上述我们介绍过,这里强调一下特殊情况,
1.当cur==_root时,特殊处理一下,直接删掉根节点置空。
2.当_minright==_pminright时,这表明要删除的节点的右节点没有左孩子节点了,特殊处理,这这交换之后直接删掉有节点置空。
3.当cur==parent说明要删除的节点为头节点并且minright==pminright,特殊处理,交换值之后进行直接指向minright的右节点即可。
bool Erase(const T&key){if (_root==nullptr){return false;}else{node<T>* cur = _root;node<T>* parent = _root;while (cur){if (cur->_val > key){parent = cur;cur = cur->_left;}else if (cur->_val < key){parent = cur;cur = cur->_right;}else{break;}}if (cur == nullptr)return false;if (cur == _root && cur->_left == nullptr && cur->_right == nullptr){delete _root;_root = nullptr;}else if(cur->_left==nullptr&&cur->_right==nullptr)//左右孩子都为空{//不确定哪边孩子if (parent->_val > key)//左孩子{parent->_left = nullptr;delete cur;}else{parent->_right = nullptr;delete cur;cur = nullptr;}return true;}else if (cur->_left == nullptr)//左孩子为空{if (parent->_val > key)//左孩子{parent->_left = cur->_right;delete cur;cur = nullptr;}else{parent->_right = cur->_right;delete cur;cur = nullptr;}return true;}else if (cur->_right == nullptr){if (parent->_val > key)//左孩子{parent->_left = cur->_left;delete cur;cur = nullptr;}else{parent->_right = cur->_left;delete cur;cur = nullptr;}return true;}else{//找到右孩子的最小auto pminright = cur->_right;auto minright = cur->_right;while (minright->_left != nullptr){pminright = minright;minright = minright->_left;}swap(minright->_val, cur->_val);if (cur == parent && pminright == minright){cur->_right = minright->_right;delete minright;minright = nullptr;}else if (pminright == minright){delete minright;minright = nullptr;}else{delete pminright->_left;pminright->_left = nullptr;}}}return true;}8.析构函数
析构函数应该是后续析构,不然删除根节点无法找到子节点,我们类似的简单想,应该先去左子树或者右子树去删除,假设只有三个节点,先去左子树,然后删除左子树,再去右子树,删除右子树,最后析构根节点。所以递归的结构就能写出来
void shanchu(node<T>* root){if (root == nullptr)return;shanchu(root->_left);shanchu(root->_right);delete root;}9.拷贝构造函数
拷贝构造是先序构造,先构造一个值相等的根节点,再去构造左子树,最后构造右子树,递归结构也可以这样写出:
node<T>* copy(node<T>* root){if (root == nullptr){return nullptr;}node<T>* nroot = new node<T>(root->_val);//构造根节点。nroot->_left=copy(root->_left);//构造左节点nroot->_right=copy(root->_right);//构造右节点。return nroot;}10.赋值运算符的重载
在进行重载时,要特别注意浅拷贝。去复用拷贝构造即可。
BSTREE operator=(BSTREE<T>& t){*this(t);return *this;}下面给出整个的二叉搜索树key的实现代码方便查阅:
#pragma once
#include<iostream>
using namespace std;
namespace zb
{template<class T>struct node{node(const T& data ){_left = _right = nullptr;_val = data;}node<T>* _left;node<T>* _right;T _val = 0;};template<class T>class BSTREE{public:BSTREE(){}BSTREE(const BSTREE<T>& t){_root=copy(t._root);}~BSTREE()//左右根{shanchu(_root);_root = nullptr;}BSTREE operator=(BSTREE<T>& t){*this(t);return *this;}bool Insert(const T& key){if (_root == nullptr){auto root = new node<T>(key);_root = root;return true;}node<T>* parent = _root;node<T>* cur = _root;while (cur != nullptr){if (cur->_val > key){parent = cur;cur = cur->_left;}else if (cur->_val < key){parent = cur;cur = cur->_right;}else{return false;}}/*cur->_val = key;*///理解一下这里为什么不对。。。原因是cur是空指针,对空指针赋值我简直太聪明了cur = new node<T>(key);if (parent->_val > key){parent->_left = cur;}else{parent->_right = cur;}return true;}node<T>* Find(const T& key){if (_root==nullptr){return nullptr;}else{auto cur = _root;while (cur!=nullptr){if (cur->_val > key){cur = cur->_left;}else if (cur->_val < key){cur = cur->_right;}else{return cur;}}}return nullptr;}void InOrder(){_InOrder(_root);cout << endl;}bool Erase(const T&key){if (_root==nullptr){return false;}else{node<T>* cur = _root;node<T>* parent = _root;while (cur){if (cur->_val > key){parent = cur;cur = cur->_left;}else if (cur->_val < key){parent = cur;cur = cur->_right;}else{break;}}if (cur == nullptr)return false;if (cur == _root && cur->_left == nullptr && cur->_right == nullptr){delete _root;_root = nullptr;}else if(cur->_left==nullptr&&cur->_right==nullptr)//左右孩子都为空{//不确定哪边孩子if (parent->_val > key)//左孩子{parent->_left = nullptr;delete cur;}else{parent->_right = nullptr;delete cur;cur = nullptr;}return true;}else if (cur->_left == nullptr)//左孩子为空{if (parent->_val > key)//左孩子{parent->_left = cur->_right;delete cur;cur = nullptr;}else{parent->_right = cur->_right;delete cur;cur = nullptr;}return true;}else if (cur->_right == nullptr){if (parent->_val > key)//左孩子{parent->_left = cur->_left;delete cur;cur = nullptr;}else{parent->_right = cur->_left;delete cur;cur = nullptr;}return true;}else{//找到右孩子的最小auto pminright = cur->_right;auto minright = cur->_right;while (minright->_left != nullptr){pminright = minright;minright = minright->_left;}swap(minright->_val, cur->_val);if (cur == parent && pminright == minright){cur->_right = minright->_right;delete minright;minright = nullptr;}else if (pminright == minright){delete minright;minright = nullptr;}else{delete pminright->_left;pminright->_left = nullptr;}}}return true;}private:void _InOrder(node<T>* root)//中序遍历{if (root==nullptr){return ;}_InOrder(root->_left);cout << root->_val<<" ";_InOrder(root->_right);}void shanchu(node<T>* root){if (root == nullptr)return;shanchu(root->_left);shanchu(root->_right);delete root;}node<T>* copy(node<T>* root){if (root == nullptr){return nullptr;}node<T>* nroot = new node<T>(root->_val);//构造根节点。nroot->_left=copy(root->_left);//构造左节点nroot->_right=copy(root->_right);//构造右节点。return nroot;}private:node<T>* _root = nullptr;};
}3.⼆叉搜索树key和key/value使⽤场景
最后再介绍一下key/value的使用场景,这个本质是多存储一个value值。可以实现以下诸多操作:
