当前位置：首页 > news >正文

卡方检验（Chi-square test）

news 来源：原创 2025/4/24 10:08:13

卡方检验的发明者为英国数学家卡尔·皮尔逊，他认为需要一种方法来描述统计样本的实际观测值与理论推断值之间的吻合程度，即用以测定观察值与预期值之间的差异显著性，遂于1900年发布了著名的统计量，卡方检验提出后得到了广泛的应用，在现代统计理论中占有重要地位.

1 什么是卡方检验？

卡方检验（Chi-Square Test）是一类基于卡方分布的假设检验方法，常用于检验两个离散变量是否存在关联（独立性检验）、理论分布与观测分布是否一致（适配度检验）

在卡方检验中，最常见的有以下两种场景：

1. 卡方独立性检验（Chi-Square Test of Independence）：

检验两个分类变量（离散型变量）之间是否存在统计学上的关联。
常见于列联表分析（Contingency Table），又称卡方列联表分析。
例如，研究“性别”与“是否违约”之间是否有显著关系。

2. 卡方适配度检验（Chi-Square Goodness-of-Fit Test）：

检验一组观测值与某一理论分布（或期望比率）是否匹配。
例如，某金融机构认为借款人违约率应当符合“某理论比例”，但实际统计发现违约率存在偏差，需要验证差异是否显著。

卡方分布简介

定义：若随机变量 $Z_{i}\sim N(0,1)$ （独立同分布的标准正态分布），则

服从自由度为 k 的卡方分布，记作 $\chi^2(k)$ 。

其均值为k，方差为2k。

性质：卡方分布是一种偏度较大的分布，随自由度增加，它逐渐变得更接近正态分布。

2 卡方独立性检验

2.1 适用场景

用于判定两个离散型变量是否存在统计学上的显著关联；
数据通常以 “ 列联表（Contingency Table）” 表示，例如：

这里 n 11 , n 12 , n 21 , n 22 表示观测频数。

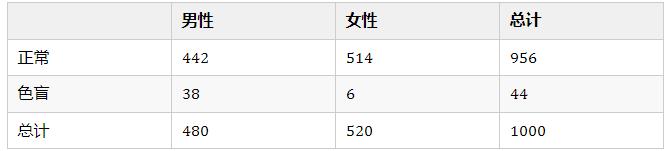
比如说，我们要研究色盲与性别这两个分类变量是否有关，就可以对人群进行抽样，得到如下列联表:

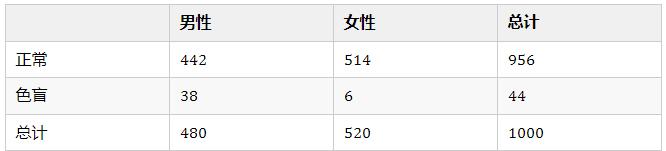
我们可以从表中直观地观察出这样一个事实：男性人群的色盲比例明显高于女性，这似乎可以支持我们提出一个合理的猜想:色盲与性别是有关的。

2.2 假设什么？- 原假设与备择假设

所谓“假设检验”首先就必须先提出假设，这里就涉及到一个问题：我们应该提出怎样的假设？这里提出原假设（null hypothesis，也称为零假设）和备择假设的概念：原假设是备择假设的对立面，同时遵循如下原则：

原假设通常是研究者想收集证据予以推翻的假设，而备择假设则是研究者想收集证据予以支持的假设.所以一般是先假设两个随机变量无关，即相互独立.

原假设H0：两个变量相互独立，即无显著关联；
备择假设H1：两个变量存在依赖关系，即存在显著关联。

相似的思想在法律中也有应用，法律的“疑罪从无”原则指的是如果没有证据就不能判一个人有罪.因此我们一般会提出原假设：这个人无罪，要说明他有罪，控方就必须提供充足的证据来推翻原假设。

根据这个原则，在上述“色盲与性别的关系”案例中，我们提出的原假设就应该是：

H₀ ：色盲与性别无关.

2.3 如何检验？- 检验统计量

卡方独立性检验的统计量通常构造如下：

1. 计算列联表中每个单元格的观测频数 $O_{_{ij}}$ 和 期望频数 $E_{ij}$

期望频数常用“独立性假设”下的估计：

2. 卡方统计量：

3. 自由度（degree of freedom, df）：

其中 r 是行数、c 是列数。

4. 根据卡方分布表或 p 值进行决策。

2.4 决策原则

给定显著性水平 $\alpha$ （常见取 0.05），若计算的 $\chi ^{^{2}}$ 统计量对应的 p 值 < $\alpha$ ，则拒绝原假设（认为两变量有关联）。

2.5 例子

已经提出假设（H₀ ：色盲与性别无关），接下来便是研究该如何“检验”。还是以色盲与性别的关系为例，由于检验的基本原理是基于原假设收集数据，从而测定观察值与预期值之间的差异显著性.因此我们的预期值应当是基于“色盲”与“性别”相互独立得到的，即：两个分类的交叉项的概率可以根据独立事件的概率乘法公式

得到：

具体而言，在这1000个人中，有：

那么想要计算出预期值，只要把上面这四个概率分别乘以样本总数1000就可以了，于是我们得到了理论频数表（括号内为观察值）：

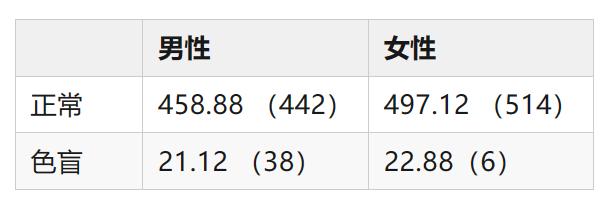
显然，四个单元格中的数据和括号内的数据有一定差距。如果原假设成立，它们应该相差不远。这个“相差不远”该如何用数据去衡量呢？容易想到用每一栏中观察值与期望值差的平方和来描述。

但是这样会产生一个问题：这个指标与每一栏自身的样本容量有关，不同的样本其基数是不一样的。换言之，这里需要的是一个相对量而不是绝对量。因此我们还要将求和公式中的每一个平方项除以这一栏的预期值：

这里构造的就是皮尔逊发布的著名统计量，也即列联表的卡方检验公式。

根据这个公式，我们可以计算出上述案例的值：

那么，这个值该怎么用呢？

在这里，我们需要简单了解一下卡方分布，其中对其严格的数学推导还需同学们深入学习。

如图给出了卡方分布的概率密度函数图，其中 n 称为自由度，其值与独立变量的个数有关。在我们本文中研究的列联表中，n 的取值为1。与正态分布类似，卡方分布的概率密度曲线下的面积都是1。

注：显著性水平是：估计总体参数落在某一区间内，可能犯错误的概率，用α表示。

显著性水平是研究者设定的阈值，用于判断卡方检验结果是否拒绝原假设。通常设定为0.05，即当p值小于0.05时，认为检验结果具有统计学意义，可以拒绝原假设。

当α和n给定时，可查表得到 $X_{n}^{2}(\alpha )$ 的值。如 $X_{5}^{2}(0.05) = 11.0705$ 等。

这个临界值的含义是：在成立时，值大于临界值的概率只有0.05，而我们刚刚计算出的数值，这说明在一次试验中发生了小概率事件，这与小概率原理矛盾.也就是说，我们可以推断“:色盲与性别无关”成立的可能性小于5%.或者说，我们可以拒绝，同时有95%的把握认为“色盲与性别有关”.

4 似曾相识的逻辑

聪明的同学可能已经发现了，卡方检验的方法其实就类似于反证法.

实际上，这两者既有联系也有区别.卡方检验先假设两变量独立，然后构造一个事件（具体来说该事件指的是皮尔逊检验统计量大于给定显著性水平下的临界值），它在我们的假设之下发生的概率极小（即为）.如果它在实际情况中发生了，就与小概率原理矛盾，因此我们便可以拒绝原假设.这个过程和反证法的步骤是类似的.

需要注意的是，小概率事件确实在一次试验中几乎不可能发生，但这并不代表着在一次试验中它一定不发生，所以我们作出“拒绝原假设”的结论是有一定的犯错误概率的.而我们知道数学中的反证法只要逻辑正确是一定可以否定初始假设的命题的.因此，卡方检验并不完全是反证法，它是一种“基于概率性质的反证法”.

3. 卡方适配度检验

3.1 适用场景

用于检验某个观测频数分布是否与理论分布或期望比例一致；
例如：
- 骰子投掷6种结果的观测比率是否与“均匀分布”匹配；
- 某金融风控模型预测客户违约率为 5%，但实际观测违约率不同，需要检验差异是否显著。

3.2 原假设与备择假设

原假设 $H_0$ ：观测分布与理论分布无显著差异，或者说观测数据符合理论分布；
备择假设 $H_1$ ：观测分布与理论分布存在显著差异。

3.3 检验统计量

1. 设有 k 种类型的结果， $O_i$ 表示观测频数， $E_i$ 表示理论频数。

2.卡方统计量：

$\chi^2 = \sum_{i=1}^{k} \frac{(O_i - E_i)^2}{E_i}$

3. 自由度：

d f = k − 1 − (被估计的分布参数数目)

如果理论分布中参数（如均值、方差等）是由数据估计得到的，需要相应地减少自由度。
4. 与卡方分布进行比较或计算 p 值，做出决策：若 $\chi^2$ 较大或 p 值 < $\alpha$ ，拒绝原假设。

4 python实现

Python 的 scipy 库中为卡方检验提供了常用的函数，如：

scipy.stats.chi2_contingency：适用于独立性检验和R×C 列联表的分析；
scipy.stats.chisquare：适用于适配度检验（一维频数对比），也可用于单行或单列的列联分析。

4.1 独立性检验示例（chi2_contingency）

import numpy as np
from scipy.stats import chi2_contingency# 1. 构造列联表数据
# 假设我们想研究“是否逾期”与“性别”之间是否相关
# 行：性别 (Male / Female)
# 列：是否逾期 (Overdue / NotOverdue)
contingency_table = np.array([[30, 70],  # 男性: 逾期=30, 未逾期=70[20, 80]   # 女性: 逾期=20, 未逾期=80
])# 2. 进行卡方独立性检验
chi2, p_value, dof, expected = chi2_contingency(contingency_table)print("Chi-square statistic:", chi2)
print("p-value:", p_value)
print("Degrees of freedom:", dof)
print("Expected frequencies:\n", expected)

输入：contingency_table 是 2×2 的列联表。
输出：
- chi2：卡方检验统计量；
- p_value：显著性水平下的 p 值；
- dof：自由度；
- expected：理论频数（若变量独立的话）。

如果 p_value < 0.05（例如），可拒绝原假设，认为性别与逾期存在显著关联。

4.2 适配度检测实例（chisquare）

import numpy as np
from scipy.stats import chisquare# 1. 观测频数
observed = np.array([50, 30, 20])  # 某三类情况的观测频数# 2. 理论频数（期望频数）
expected = np.array([45, 35, 20])  # 理论上或经验上预估的频数# 3. 卡方适配度检验
chi2_stat, p_value = chisquare(f_obs=observed, f_exp=expected)print("Chi-square statistic:", chi2_stat)
print("p-value:", p_value)