当前位置：首页 > news >正文

LeetCode-417. 太平洋大西洋水流问题

news 来源：原创 2025/4/24 12:14:16

1、题目描述

有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回网格坐标 result 的 2D 列表 ，其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

示例 1：

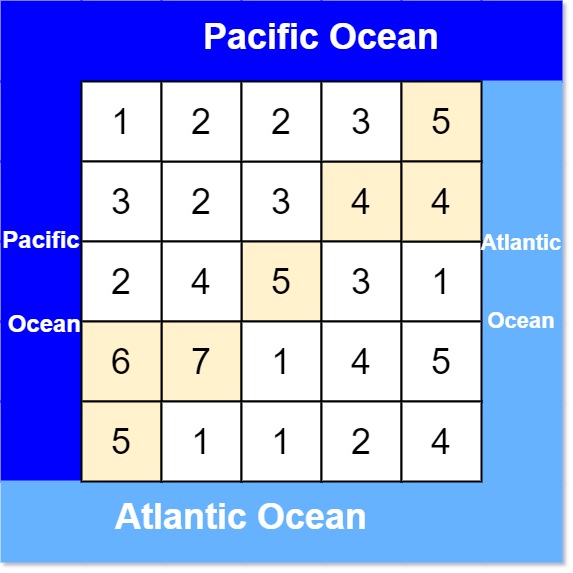
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

示例 2：

输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]

提示：

m == heights.length
n == heights[r].length
1 <= m, n <= 200
0 <= heights[r][c] <= 105

2、代码：

#include <queue>
#include <vector>using namespace std;class Solution
{
public:// 主函数，找出既能流向太平洋又能流向大西洋的坐标vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights){vector<vector<int>> result;int m = heights.size();if (m <= 0)return result;int n = heights[0].size();if (n <= 0)return result;// 初始化访问标记数组，分别记录能到达太平洋和大西洋的点vector<vector<bool>> pacific(m, vector<bool>(n, false));vector<vector<bool>> atlantic(m, vector<bool>(n, false));queue<pair<int, int>> q; // BFS队列// 处理太平洋的边界：上边缘和左边缘// 上边缘（第一行）for (int i = 0; i < n; ++i) {pacific[0][i] = true;q.push({0, i});}// 左边缘（第一列）for (int j = 0; j < m; ++j) {pacific[j][0] = true;q.push({j, 0});}// BFS扩展，标记所有能流入太平洋的点bfs(pacific, heights, q);// 处理大西洋的边界：下边缘和右边缘// 下边缘（最后一行）for (int i = 0; i < n; ++i) {atlantic[m - 1][i] = true;q.push({m - 1, i});}// 右边缘（最后一列）for (int j = 0; j < m; ++j) {atlantic[j][n - 1] = true;q.push({j, n - 1});}// BFS扩展，标记所有能流入大西洋的点bfs(atlantic, heights, q);// 遍历所有点，找出同时能到达太平洋和大西洋的点for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {if (pacific[i][j] && atlantic[i][j]) {result.push_back({i, j});}}}return result;}private:// 广度优先搜索，从队列中的点出发，扩展标记所有可达的高点// visited: 引用传递的访问标记数组，记录能流入某个海洋的点// heights: 输入的地形高度数组// q: 队列，初始时包含边界点，处理过程中存储待扩展的点void bfs(vector<vector<bool>>& visited, vector<vector<int>>& heights,queue<pair<int, int>>& q){// 四个方向的偏移量：上、下、左、右int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};int m = heights.size();int n = heights[0].size();while (!q.empty()) {auto [row, col] = q.front();q.pop();// 遍历四个方向for (auto& dir : dirs) {int nr = row + dir[0]; // 新的行坐标int nc = col + dir[1]; // 新的列坐标// 检查新坐标是否在矩阵范围内// 且未被访问过// 且新坐标的高度 >= 当前点的高度（保证水流可以逆流而上）if (nr >= 0 && nr < m && nc >= 0 && nc < n &&!visited[nr][nc] && heights[nr][nc] >= heights[row][col]) {visited[nr][nc] = true; // 标记为可到达q.push({nr, nc});       // 加入队列继续扩展}}}}
};