动态规划dp专题-（下）

🎯四、区间DP

（1）石子合并-模版题

（2） 2806. 涂色 - AcWing题库

（3）遥远的雪国列车

🎯五、买卖股票系列 ※

（1）121. 买卖股票的最佳时机 - 力扣 --，股票只能买卖一次，问最大利润

（2）122. 买卖股票的最佳时机 II - 力扣 --可以多次买卖股票，问最大收益

（3）123. 买卖股票的最佳时机 III -  --最多买卖两次，问最大收益

（4）188. 买卖股票的最佳时机 IV - 力扣 --最多买卖k笔交易，问最大收益--- 123的进阶版

（5）309. 买卖股票的最佳时机含冷冻期 - 力扣 --可以多次买卖但每次卖出有冷冻期1天。

（6）714. 买卖股票的最佳时机含手续费 - 力扣可以多次买卖，但每次有手续费

---

🎯四、区间DP

什么是区间dp?

dp的定义及转移方程？

dp[i][j]，其中i和j分别表示区间的起点和终点

推导状态转移方程：

      1、  分析问题的划分方式：思考如何将大区间划分为更小的区间。这需要根据问题的特点来确定，常见的划分方式是在区间内选择一个分割点k，将区间[i, j]分成[i, k]和[k + 1, j]两个子区间。

      2、构建状态转移关系：根据问题的要求，结合划分后的子区间状态，构建状态转移方程。

遍历顺序？如何枚举区间？？模版？

 所以正确的枚举方法应该为：

for (int len = 2; len <= n; len++) {         // 先枚举区间长度for (int i = 1; i + len - 1 <= n; i++) { // 枚举左点int j = i + len - 1;                 // 区间右端点for (int k = i; k <= j; k++) {        // 枚举分割点，构造状态转移方程//dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + w[i][j]);}}
}

---

（1）石子合并-模版题

【acwing】动态规划系列_acwing memset dp-CSDN博客  -----blog中最后一道题

#include<bits/stdc++.h>
using namespace std;
const int N=210;
int dp[N][N];
int a[N];
int sum[N];//存储前缀和
int main()
{int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];sum[i]=sum[i-1]+a[i];}//枚举区间for(int len=2;len<=n;len++){for(int i=1;i+len-1<=n;i++) //枚举左端点{int l=i;//左端点int r=i+len-1;//区间右端点dp[l][r]=INT_MAX; //初始化一个很大的值，方便后续取最小值操作for(int j=l;j<=r;j++) //枚举区间分割点{dp[l][r]=min(dp[l][r],dp[l][j]+dp[j+1][r]+sum[r]-sum[l-1]);}}}cout<<dp[1][n];return 0;
}

纯模版题，区间dp的入门题，自己写的时候忘了初始化dp[l][r] 为一个很大的值了

dp[l][r] 表示将区间 [l,r] 内的石子合并成一堆的最小代价

（2） 2806. 涂色 - AcWing题库

 ①定义dp：dp[l][r]:表示将区间 [l,r]染成目标颜色最少需要的染色次数

②状态转移：

比较难以理解的是端点颜色相同的情况：

#include <bits/stdc++.h>
using namespace std;
const int N = 60;
int dp[N][N];
char s[N];int main() {cin>>s+1;int n=strlen(s+1);for (int i = 1; i <= n; i++) {dp[i][i] =1; }// 动态规划for (int len = 2; len <= n; len++) { for (int l = 1; l + len - 1 <= n; l++) { int r = l + len - 1; dp[l][r] = INT_MAX; if (s[l] == s[r]) {dp[l][r] = min(dp[l+1][r],dp[l][r-1]);}for (int k = l; k < r; k++) { // 遍历分割点dp[l][r] = min(dp[l][r], dp[l][k] + dp[k + 1][r] );}}}cout << dp[1][n]; return 0;
}

（3）遥远的雪国列车

    ​​​​​

题目好有趣，自己分析的话其实也能想到转移方程怎么写

看这张图：

 

#include <bits/stdc++.h>
using namespace std;int main() {ios::sync_with_stdio(0);cin.tie(0);int n, m, q;cin >> n >> m >> q;vector<vector<int>> dp(n + 1, vector<int>(n + 1, 0)); // 使用1-based索引// 读取m条边并初始化dpfor (int i = 0; i < m; i++) {int x, y;cin >> x >> y;dp[x][y] += 1; // 注意！！！同一区间可以停多个}// 动态规划预处理区间和for (int len = 2; len <= n; len++) {        // 区间长度从2到nfor (int l = 1; l + len - 1 <= n; l++) { // 左端点lint r = l + len - 1;               // 右端点r// 合并子区间并减去重叠部分，累加到当前区间dp[l][r] += dp[l][r - 1] + dp[l + 1][r] - dp[l + 1][r - 1];}}// 处理查询while (q--) {int l, r;cin >> l >> r;cout << dp[l][r] << endl;}return 0;
}

🎯五、买卖股票系列 ※

（1）121. 买卖股票的最佳时机 - 力扣 --，股票只能买卖一次，问最大利润

 方法一：暴力找最大间距（n*n）

方法二：贪心（n）:取最左最小值，取最右最大值，那么得到的差值就是最大利润。

class Solution {
public:int maxProfit(vector<int>& prices) {int low = INT_MAX;int result = 0;for (int i = 0; i < prices.size(); i++) {low = min(low, prices[i]);  // 取最左最小价格result = max(result, prices[i] - low); // 直接取最大区间利润}return result;}
};

方法三：动态规划（n）

①定义数组：dp[i][0] 表示第i天持有股票所得最多现金；dp[i][1] 表示第i天不持有股票所得最多现金。【“持有”，“持有”不代表就是当天“买入”！也有可能是昨天就买入了，今天保持持有的状态】

②递推方程：

③初始化; dp[0][0]表示第0天持有股票，此时的持有股票就一定是买入股票了，因为不可能有前一天推出来，所以dp[0][0] -= prices[0];

        p[0][1]表示第0天不持有股票，不持有股票那么现金就是0，所以dp[0][1] = 0;

④遍历顺序：dp[i]都是由dp[i - 1]推导出来的，那么一定是从前向后遍历

⑤举例：

dp[5][1]就是最终结果（卖出之后的，一定不持有股票），注意0_based索引

class Solution {
public:int maxProfit(vector<int>& prices) {//定义dp数组vector<vector<int>> dp(prices.size(),vector<int>(2,0));//初始化dp[0][0]=-prices[0];dp[0][1]=0;//dpfor(int i=1;i<prices.size();i++){dp[i][0]=max(dp[i-1][0],-prices[i]);dp[i][1]=max(dp[i-1][0]+prices[i],dp[i-1][1]);}return dp[prices.size()-1][1];}
};

        感觉自己要是第一遍写肯定暴力，，，想不到这样的dp写法 

（2）122. 买卖股票的最佳时机 II - 力扣 --可以多次买卖股票，问最大收益

        本题和121. 买卖股票的最佳时机 (opens new window)的唯一区别是本题股票可以买卖多次了（注意只有一只股票，所以再次购买前要出售掉之前的股票）

① 这里重申一下dp数组的含义：

• dp[i][0] 表示第i天持有股票所得现金。
• dp[i][1] 表示第i天不持有股票所得最多现金

②递推方程：

class Solution {
public:int maxProfit(vector<int>& prices) {//定义dp数组vector<vector<int>> dp(prices.size(),vector<int>(2,0));//初始化dp[0][0]=-prices[0];dp[0][1]=0;//dpfor(int i=1;i<prices.size();i++){dp[i][0]=max(dp[i-1][0],dp[i-1][1]-prices[i]);//唯一不同的地方dp[i][1]=max(dp[i-1][0]+prices[i],dp[i-1][1]);}return dp[prices.size()-1][1];}
};

（3）123. 买卖股票的最佳时机 III - --最多买卖两次，问最大收益

 ①dp数组含义：

dp[i][j]中 i表示第i天，j为 [0 - 4] 五个状态，dp[i][j]表示第i天状态j所剩最大现金

②递推公式

③初始化：

④举例;

两次卖出的状态现金最大一定是最后一次卖出 dp[4][4]

class Solution {
public:int maxProfit(vector<int>& prices) {vector<vector<int>> dp(prices.size(), vector<int>(5, 0));dp[0][1] = -prices[0];dp[0][3] = -prices[0];for (int i = 1; i < prices.size(); i++) {dp[i][0] = dp[i - 1][0];dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);}return dp[prices.size() - 1][4];}
};

（4）188. 买卖股票的最佳时机 IV - 力扣 --最多买卖k笔交易，问最大收益--- 123的进阶版

 ①dp含义：dp[i][j] --第i天的状态为j，所剩下的最大现金是dp[i][j]

除了0以外，偶数就是卖出，奇数就是买入，至多K笔交易，那么 j 的范围就定义为 2 * k + 1 

②递推方程

③初始化

④ 举例：

class Solution {
public:int maxProfit(int k, vector<int>& prices) {vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));for (int j = 1; j < 2 * k; j += 2) {dp[0][j] = -prices[0];}for (int i = 1;i < prices.size(); i++) {for (int j = 0; j < 2 * k - 1; j += 2) {dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);}}return dp[prices.size() - 1][2 * k];}
};

（5）309. 买卖股票的最佳时机含冷冻期 - 力扣 --可以多次买卖但每次卖出有冷冻期1天。

dp[i][j]，第i天状态为j，所剩的最多现金为dp[i][j]。 

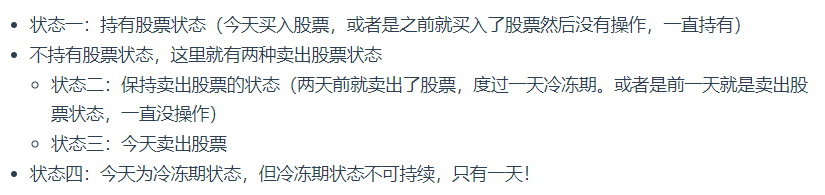
j有四种情况

②递推：

③初始化：

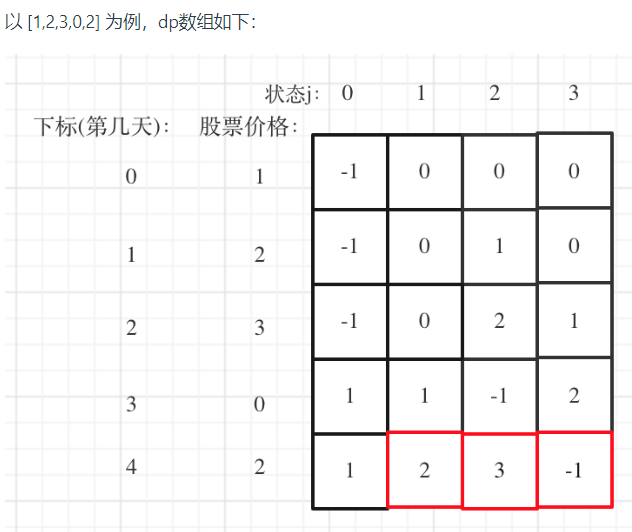
④举例

最后结果是取 状态二，状态三，和状态四的最大值，不少同学会把状态四忘了，状态四是冷冻期，最后一天如果是冷冻期也可能是最大值

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();if (n == 0) return 0;vector<vector<int>> dp(n, vector<int>(4, 0));dp[0][0] -= prices[0]; // 持股票for (int i = 1; i < n; i++) {dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]));dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);dp[i][2] = dp[i - 1][0] + prices[i];dp[i][3] = dp[i - 1][2];}return max(dp[n - 1][3], max(dp[n - 1][1], dp[n - 1][2]));}
};

（6）714. 买卖股票的最佳时机含手续费 - 力扣可以多次买卖，但每次有手续费

相对于动态规划：122.买卖股票的最佳时机II (opens new window)，本题只需要在计算卖出操作的时候减去手续费就可以了，代码是一样的

class Solution {
public:int maxProfit(vector<int>& prices,int fee) {//定义dp数组vector<vector<int>> dp(prices.size(),vector<int>(2,0));//初始化dp[0][0]=-prices[0];dp[0][1]=0;//dpfor(int i=1;i<prices.size();i++){dp[i][0]=max(dp[i-1][0],dp[i-1][1]-prices[i]);//唯一不同的地方dp[i][1]=max(dp[i-1][0]+prices[i]-fee,dp[i-1][1]);}return dp[prices.size()-1][1];}
};