当前位置：首页 > news >正文

从对数变换到深度框架：逻辑回归与交叉熵的数学原理及PyTorch实战

news 来源：原创 2025/4/25 9:58:51

前言
一、连乘变连加
二、最小化损失函数
2.1交叉熵
2.2 二分类交叉熵
2.3 多分类交叉熵
三、逻辑回归与二分类
3.1 逻辑回归与二分类算法理论讲解
3.1.1 散点输入
3.1.2 前向计算
3.1.3 Sigmoid函数引入
3.1.4 参数初始化
3.1.5 损失函数
3.1.6 开始迭代
3.1.7 梯度下降显示
四、基于框架的逻辑回归
4.1实验原理
4.1.1 数据输入
4.1.2 定义前向模型
4.1.3 定义损失函数和优化器
4.1.4 更新模型参数并显示
4.1.5 pytroch 实现 sigmoid +二元交叉熵代码
4.1.6 softmax+多元交叉熵代码
总结

前言

书接上文

深度学习激活函数与损失函数全解析：从Sigmoid到交叉熵的数学原理与实践应用-CSDN博客文章浏览阅读254次，点赞10次，收藏8次。本文系统探讨了Sigmoid、tanh、ReLU、Leaky ReLU、PReLU、ELU等激活函数的数学公式、导数特性、优劣势及适用场景，并通过Python代码实现可视化分析。同时深入对比了极大似然估计与交叉熵损失函数的差异，阐述其在分类任务中的核心作用，揭示MSE在分类问题中的局限性及交叉熵的理论优势。https://blog.csdn.net/qq_58364361/article/details/147440791?fromshare=blogdetail&sharetype=blogdetail&sharerId=147440791&sharerefer=PC&sharesource=qq_58364361&sharefrom=from_link

一、连乘变连加

通过取对数(log的底数为e)，将连乘变成连加，方便计算。

将xi带入得到如下公式：

对上面求导，然后通过求导数，令导数等于零来解方程，找到使得对数似然函数最大化的参数值p。

二、最小化损失函数

2.1交叉熵

交叉熵（Cross Entropy）是一种用于衡量两个概率分布之间差异的度量方法。在机器学习中，交叉熵常用于衡量模型的预测结果与真实标签之间的差异，交叉熵越小，两个概率分布就越接近，即拟合的更好。

交叉熵的计算公式

通过上面的讲解，发现对极大似然估计公式前面加上负号，使用负对数似然函数来定义损失函数和交叉熵公式一样（通常称为交叉熵损失函数），这样就将最大化似然函数转化为最小化损失函数的问题。这样，在求解优化问题时，可以使用梯度下降等优化算法来最小化负对数似然函数（或交叉熵损失函数），从而得到最大似然估计的参数值。

2.2 二分类交叉熵

在二分类情况下，模型最后需要预测的结果只有两种情况，对于每个类别我们的预测得到的概率为p和1-p,此时表示式为(log的底数为e):

N表示实验次数也相当于样本数

2.3 多分类交叉熵

多分类交叉熵就是对二分类的交叉熵的扩展，在计算公式中和二分类稍微有些区别，但是还是比较容易理解，具体公式如下所示：

补充：交叉熵怎么衡量损失的。

如果预测的概率值接近1 损失小，如果预测的概率值接近于0损失大，可以通过softmax(把数值转换成概率)再结合交叉熵就能做分类损失函数。

三、逻辑回归与二分类

从以下3个方面对逻辑回归与二分类进行介绍
1.逻辑回归与二分类算法理论讲解
2.编程实例与步骤
3.实验现象
上面这3方面的内容，让大家，掌握并理解逻辑回归与二分类。

3.1 逻辑回归与二分类算法理论讲解

这节学习逻辑回归和二分类问题，在前面课程学了如何使用交叉熵这个损失函数来实现分类问题理论。

节就用一下交叉熵损失函数，来实现逻辑回归的问题。

3.1.1 散点输入

在本实验中，给出了如下两类散点，其分布如下图所示：

输入两个值，一个是x1 ,x2 输出是两类一类是红色点，一个是蓝色点。

3.1.2 前向计算

本实验中的前向计算与前面的所有章节都不同，因为本实验的输入特征是两个，所以给出输出公式为：

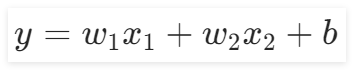
。在“前向计算”组件中，我们可以通过修改

的值来查看对应的直线。

3.1.3 Sigmoid函数引入

确定好线性函数公式之后，二分类的激活函数可以用Sigmoid和Softmax,这里使用Sigmoid函数作为它的输出。

如下图所示。

3.1.4 参数初始化

在“参数初始化”组件中，可以初始化两个输入特征、以及偏置b，还有学习率。由于输入特征的增加，并且使用了激活函数激活，这里的学习率会比较大一点。

3.1.5 损失函数

在本实验中，选用交叉熵损失函数作为损失函数。因为交叉熵比均方差更适合分类问题，而均方差比交叉熵更适合回归问题。

在上一章节中，得到了交叉熵的表达式为：

将其激活后的函数带入交叉熵中，得到：

wx+b能得到一个数值，这个数值经过Sigmoid就变成了概率，带入交叉熵损失就能计算了。

3.1.6 开始迭代

反向传播开始前，需要设置好迭代次数，本实验提供了“开始迭代”组件，用来设置迭代次数，次数越高，模型的效果就越好。

接下来就是反向传播的过程，其中参数的更新同样使用的是梯度下降，也就意味着要令损失函数对参数进行求导，其结果如下图所示：

推导一下

3.1.7 梯度下降显示

接着通过“梯度下降显示”组件显示迭代过程中返回的参数值和损失值，该组件的内容如下图所示：

代完成后，我们就可以通过这个模型来预测未知的数据属于哪一类了。

import numpy as np
import matplotlib.pyplot as plt# 1.散点输入
# 表示红色点
class1_points = np.array([[1.9, 1.2],[1.5, 2.1],[1.9, 0.5],[1.5, 0.9],[0.9, 1.2],[1.1, 1.7],[1.4, 1.1]])
# 表示是绿色点
class2_points = np.array([[3.2, 3.2],[3.7, 2.9],[3.2, 2.6],[1.7, 3.3],[3.4, 2.6],[4.1, 2.3],[3.0, 2.9]])
# 2提取两类特征输入维度为2
x1_data = np.concatenate((class1_points[:, 0], class2_points[:, 0]), axis=0)
x2_data = np.concatenate((class1_points[:, 1], class2_points[:, 1]), axis=0)
# 添加标签
label = np.concatenate((np.zeros(len(class1_points)), np.ones(len(class2_points))), axis=0)
# 3参数初始化
w1 = 0.1
w2 = 0.2
b = 0
#超参数 学习率
lr = 0.05# sigmoid函数
def sigmoid(x):return 1 / (1 + np.exp(-x))  # 定义sigmoid函数，用于将线性回归的输出映射到[0,1]之间# 4.前向计算
def forward_cal(w1, w2, b):z = w1 * x1_data + w2 * x2_data + b  # 计算线性组合y_pre = sigmoid(z)  # 应用sigmoid函数得到预测值return y_pre# 5.计算损失函数
def loss_func(y_pre):loss = -np.mean(label * np.log(y_pre) + (1 - label) * np.log(1 - y_pre))  # 计算交叉熵损失return loss# 画图
fig, (ax1, ax2) = plt.subplots(2, 1)  # 创建一个包含两个子图的图表
loss_list = []  # 用于存储每轮迭代的损失值
epoch_list = []  # 用于存储每轮迭代的epoch值
epochs = 1000  # 迭代总次数
for epoch in range(1, epochs + 1):  # 开始迭代y_pre = forward_cal(w1, w2, b)  # 前向传播计算预测值loss = loss_func(y_pre)  # 计算损失deda = (y_pre - label) / (y_pre * (1 - y_pre))  # 计算损失函数的梯度dadz = y_pre * (1 - y_pre)  # 计算损失函数的梯度dzdw1 = x1_data  # 计算w1的梯度dzdw2 = x2_data  # 计算w2的梯度dzdb = 1  # 计算b的梯度gradient_w1 = np.dot(dzdw1, deda * dadz) / (len(x1_data))  # 计算w1的梯度gradient_w2 = np.dot(dzdw2, deda * dadz) / (len(x2_data))  # 计算w2的梯度gradient_b = np.mean(deda * dadz)  # 计算b的梯度w1 = w1 - lr * gradient_w1  # 更新w1w2 = w2 - lr * gradient_w2  # 更新w2b = b - lr * gradient_b  # 更新bprint(f"epoch:{epoch},loss:{loss}")  # 打印当前epoch和损失值loss_list.append(loss)  # 将损失值添加到列表中epoch_list.append(epoch)  # 将epoch值添加到列表中if epoch % 50 == 0 or epoch == 1:  # 每50轮迭代或初始迭代绘制一次图形x1_min = x1_data.min()  # 计算x1数据的最小值x1_max = x1_data.max()  # 计算x1数据的最大值x2_min = -(w1 * x1_min + b) / w2  # 计算决策边界的x坐标最小值x2_max = -(w1 * x1_max + b) / w2  # 计算决策边界的x坐标最大值ax1.clear()  # 清空ax1ax1.scatter(x1_data[:len(class1_points)], x2_data[:len(class1_points)], color='r')  # 绘制红色点ax1.scatter(x1_data[len(class1_points):], x2_data[len(class1_points):], color='b')  # 绘制蓝色点ax1.plot([x1_min, x1_max], [x2_min, x2_max], color='r')  # 绘制决策边界ax2.clear()  # 清空ax2ax2.plot(epoch_list, loss_list)  # 绘制损失随epoch变化的曲线plt.pause(1)  # 暂停1秒

四、基于框架的逻辑回归

4.1实验原理

4.1.1 数据输入

本实验中，给出了如下两类散点，其分布如下图所示：

4.1.2 定义前向模型

准备好数据之后，接着就是定义前向过程，从上一章节可以知道，逻辑回归算法实现分类时，有两个输入特征，即公式为：

。因此在“定义前向模型”组件中，需要保证输入特征数量为2，输出1个特征，使用Sigmoid()函数分成两类，即

是一类，

是一类。

讲解一下逻辑回归+二元交叉熵和softmax+多分类交叉熵的区别？

逻辑回归神经网络示意图

对计算出的结果结合二分类交叉熵进行计算损失。

eg: 实际标签为 0，预测值a为0.1

计算方式：

eg: 实际标签为 1，预测值a为0.8

softmax+普通交叉熵

输出计算公式

将输出的o1,o2,o3转换成概率

使用softmax对输出进行计算概率

对计算出的结果结合多分类交叉熵进行计算损失。

多分类交叉熵

多分类交叉熵就是对二分类的交叉熵的扩展，在计算公式中和二分类稍微有些区别，但是还是比较容易理解，具体公式如下所示：

onehot编码

例子

比如分三类有猫、狗、牛三类，真实标签是狗的话，可以表示为[0,1,0] onehot编码。真实标签是猫的话，可以表示为[1,0，0] onehot编码，真实标签是牛的话可以表示为[0,0,1]

4.1.3 定义损失函数和优化器

在选择好前向模型后，需要接着选择使用哪种损失函数和优化器，在“定义损失函数和优化器”组件中，提供的损失函数是交叉熵，优化器是SGD（随机梯度下降），学习率有多个选项，比如0.5、0.1、0.05…，建议选择较大的学习率，可以很快获得分类结果。

在参数、损失函数、优化器以及学习率选择完毕后，就可以进行迭代了。模型的参数会随着不断迭代而改变，直至迭代完毕。本实验的“开始迭代”组件中提供了如下图所示的迭代次数：

4.1.4 更新模型参数并显示

选择好迭代次数后，就需要设置一个显示频率，用来观察迭代过程中参数和损失值的变化，如下图所示：

接着就是观察迭代过程中参数和损失值的变化，通过“决策边界绘制与输出”组件即可观察，其内容如下：

4.1.5 pytroch 实现 sigmoid +二元交叉熵代码

# 导入包
# pytroch 实现  sigmoid +二元交叉熵
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optimizer
import matplotlib.pyplot as plt
# 设置一下随机数种子确保每一次运行结果一致
seed=42
torch.manual_seed(seed)
# 1散点输入
class1_points = np.array([[1.9, 1.2],[1.5, 2.1],[1.9, 0.5],[1.5, 0.9],[0.9, 1.2],[1.1, 1.7],[1.4, 1.1]])
class2_points = np.array([[3.2, 3.2],[3.7, 2.9],[3.2, 2.6],[1.7, 3.3],[3.4, 2.6],[4.1, 2.3],[3.0, 2.9]])
# 不用单独提取x1_data 和x2_data
# 框架会根据输入特征自动提取
# 2.获得训练数据和标签
x_train = np.concatenate((class1_points, class2_points), axis=0)
y_train = np.concatenate((np.zeros(len(class1_points)), np.ones(len(class2_points))))
#3.转化成张量
x_train_tensor=torch.tensor(x_train,dtype=torch.float32)
y_train_tensor=torch.tensor(y_train,dtype=torch.float32)
#4.定义前向传播模型
class LogisticRegreModel(nn.Module):#__init__def __init__(self):#继承父类super(LogisticRegreModel, self).__init__()#自定义层self.fc=nn.Linear(2,1)#forward 层def forward(self,x):x = self.fc(x)#使用激活函数， 获得sigmoid 之后的tensor值x=torch.sigmoid(x)return x
# 网络模型初始化 申请个对象 实例化网络对象
model = LogisticRegreModel()
# 5.定义损失函数和优化器
# 定义损失函数 使用二元交叉熵
cri=nn.BCELoss()
# 需要输入模型参数和学习率
lr = 0.05
optimizer = optimizer.SGD(model.parameters(), lr=lr)# 最后画图
fig, (ax1, ax2) = plt.subplots(1, 2)
# 获得右边的损失和迭代次数
epoch_list = []
epoch_loss = []
# 最后画图
# 7.迭代训练
epochs = 1000
for epoch in range(1, epochs + 1):# 前向传播进行预测y_pre = model(x_train_tensor)# 损失函数将预测结果和真实结果计算损失loss = cri(y_pre, y_train_tensor.unsqueeze(1))# 反向传播与优化# 1.第一步清空梯度optimizer.zero_grad()# 2第二步反向传播计算梯度loss.backward()# 3.参数更新optimizer.step()#展示一下假设你模型训练好了然后进行实际预测怎么得到猫和狗的类别model.eval()with torch.no_grad():pre=model(torch.tensor([[1.9, 1.2]]))list_class=['猫','狗']#tensor中.detach表示从计算图分离出一个新的张量#.cpu()表示从gpu上转到cpu#.item()转为数值max_loc=int(np.round(pre.detach().cpu().item()))print(list_class[max_loc])if epoch % 50 == 0 or epoch == 1:print(f"epoch:{epoch},loss:{loss}")# 画左图# 从模型获得w1和w2 及b的参数w1, w2 = model.fc.weight.data[0]b = model.fc.bias.data[0]# w1*x1+w2*x2+b=0# 求出斜率和截距if w2 != 0:slope = -w1 / w2intercept = -b / w2# 绘制直线 开始结束位置x_min, x_max = 0, 5x = np.array([x_min, x_max])y = slope * x + interceptax1.clear()ax1.plot(x, y, 'r')# 画散点图ax1.scatter(x_train[:len(class1_points), 0], x_train[:len(class1_points), 1])ax1.scatter(x_train[len(class1_points):, 0], x_train[len(class1_points):, 1])# 画右图ax2.clear()epoch_list.append(epoch)epoch_loss.append(loss.item())ax2.plot(epoch_list, epoch_loss, 'b')plt.pause(1)

4.1.6 softmax+多元交叉熵代码

# 导入包
# pytroch 实现  sigmoid +二元交叉熵
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optimizer
import matplotlib.pyplot as plt
# 设置一下随机数种子确保每一次运行结果一致
seed=42
torch.manual_seed(seed)
# 1散点输入
class1_points = np.array([[1.9, 1.2],[1.5, 2.1],[1.9, 0.5],[1.5, 0.9],[0.9, 1.2],[1.1, 1.7],[1.4, 1.1]])
class2_points = np.array([[3.2, 3.2],[3.7, 2.9],[3.2, 2.6],[1.7, 3.3],[3.4, 2.6],[4.1, 2.3],[3.0, 2.9]])
# 不用单独提取x1_data 和x2_data
# 框架会根据输入特征自动提取
# 2.获得训练数据和标签
x_train = np.concatenate((class1_points, class2_points), axis=0)
y_train = np.concatenate((np.zeros(len(class1_points)), np.ones(len(class2_points))))
#3.转化成张量
x_train_tensor=torch.tensor(x_train,dtype=torch.float32)
#因为softmax需要转化成onehot编码所以类型是torch.long
y_train_tensor=torch.tensor(y_train,dtype=torch.long)
#4.定义前向传播模型
class LogisticRegreModel(nn.Module):#__init__def __init__(self):#继承父类super(LogisticRegreModel, self).__init__()#自定义层 #修改成输出为2类self.fc=nn.Linear(2,2)#forward 层def forward(self,x):x = self.fc(x)return x
# 网络模型初始化 申请个对象 实例化网络对象
model = LogisticRegreModel()
# 5.定义损失函数和优化器
# 定义损失函数 使用多元交叉熵 里面包括softmax
cri=nn.CrossEntropyLoss()
# 需要输入模型参数和学习率
lr = 0.05
optimizer = optimizer.SGD(model.parameters(), lr=lr)# 最后画图
fig, (ax1, ax2) = plt.subplots(1, 2)
# 获得右边的损失和迭代次数
epoch_list = []
epoch_loss = []
# 最后画图
# 7.迭代训练
epochs = 1000
for epoch in range(1, epochs + 1):# 前向传播进行预测y_pre = model(x_train_tensor)# 损失函数将预测结果和真实结果计算损失#y_train_tensor不需要扩维度，因为交叉熵会自动转换成onehot编码loss = cri(y_pre, y_train_tensor)# 反向传播与优化# 1.第一步清空梯度optimizer.zero_grad()# 2第二步反向传播计算梯度loss.backward()# 3.参数更新optimizer.step()#展示一下假设你模型训练好了然后进行实际预测怎么得到猫和狗的类别model.eval()with torch.no_grad():#模型输出后需要softmax转化成概率值pre=torch.softmax(model(torch.tensor([[1.9, 1.2]])),dim=1)list_class=['猫','狗']#tensor中.detach表示从计算图分离出一个新的张量#.cpu()表示从gpu上转到cpu#.numpy()转为数值max_loc=np.argmax(pre.detach().cpu().numpy())print(list_class[max_loc])if epoch % 50 == 0 or epoch == 1:print(f"epoch:{epoch},loss:{loss}")# 画左图# 从模型获得w1和w2 及b的参数w1, w2 = model.fc.weight.data[0]b = model.fc.bias.data[0]# w1*x1+w2*x2+b=0# 求出斜率和截距if w2 != 0:slope = -w1 / w2intercept = -b / w2# 绘制直线 开始结束位置x_min, x_max = 0, 5x = np.array([x_min, x_max])y = slope * x + interceptax1.clear()ax1.plot(x, y, 'r')# 画散点图ax1.scatter(x_train[:len(class1_points), 0], x_train[:len(class1_points), 1])ax1.scatter(x_train[len(class1_points):, 0], x_train[len(class1_points):, 1])# 画右图ax2.clear()epoch_list.append(epoch)epoch_loss.append(loss.item())ax2.plot(epoch_list, epoch_loss, 'b')ax2.set_xlabel('epoch')ax2.set_ylabel('loss')plt.pause(1)

总结

文章围绕逻辑回归的核心数学原理展开，首先通过取对数将连乘运算转化为连加形式，简化计算；随后深入分析交叉熵及其在分类任务中的应用，揭示其与负对数似然函数的等价性，并扩展至多分类场景。核心部分以二分类问题为案例，结合Sigmoid函数、梯度下降等工具实现逻辑回归模型，同时对比二元交叉熵与Softmax多分类交叉熵的差异。最后通过PyTorch框架代码实现两类任务的训练过程，动态展示参数更新与损失变化，帮助读者理解理论到实践的完整链路。