当前位置：首页 > news >正文

哈希表的实现

news 来源：原创 2025/4/25 11:51:54

1. 哈希概念

哈希(hash)⼜称散列，是⼀种组织数据的⽅式。从译名来看，有散乱排列的意思。本质就是通过希

函数把关键字Key跟存储位置建⽴⼀个映射关系，查找时通过这个哈希函数计算出Key存储的置进⾏快速查找.

1.2 哈希冲突

这⾥存在的⼀个问题就是，两个不同的key可能会映射到同⼀个位置去，这种问题我们叫做哈希冲突，或者哈希碰撞。理想情况是找出⼀个好的哈希函数避免冲突，但是实际场景中，冲突是不可免的，所以我们尽可能设计出优秀的哈希函数，减少冲突的次数，同时也要去设计出解决冲突的方案。

1.3 负载因⼦

假设哈希表中已经映射存储了N个值，哈希表的⼤⼩为M，那么，负载因⼦有些地⽅

也翻译为载荷因⼦/装载因⼦等，他的英⽂为load factor。负载因⼦越⼤，哈希冲突的概率越⾼，空间利⽤率越⾼；负载因⼦越⼩，哈希冲突的概率越低，空间利⽤率越低；

1.4 将关键字转为整数

我们将关键字映射到数组中位置，⼀般是整数好做映射计算，如果不是整数，我们要想办法转换整

数，这个细节我们后⾯代码实现中再进⾏细节展⽰。下⾯哈希函数部分我们讨论时，如果关键字不是整数，那么我们讨论的Key是关键字转换成的整数。

2.开放定址法

在开放定址法中所有的元素都放到哈希表⾥，当⼀个关键字key⽤哈希函数计算出的位置冲突了，则按照某种规则找到⼀个没有存储数据的位置进⾏存储，开放定址法中负载因⼦⼀定是⼩于的。这⾥的规则有三种：线性探测、⼆次探测、双重探测。

2.1开放定址法，即线性探测解决冲突

2.2 开放定址法的哈希表结构

enum State

{

EXIST,

EMPTY,

DELETE

};

template < class K , class V >

struct HashData

{

pair<K, V> _kv;

State _state = EMPTY;

};

template < class K , class V >

class HashTable

{

private :

vector<HashData<K, V>> _tables;

size_t _n = 0 ; // 表中存储数据个数

};

2.3key不能取模的问题

当key是string/Date等类型时，key不能取模，那么我们需要给HashTable增加⼀个仿函数，这个仿函数⽀持把key转换成⼀个可以取模的整形，如果key可以转换为整形并且不容易冲突，那么这个仿函数就⽤默认参数即可，如果这个Key不能转换为整形，我们就需要⾃⼰实现⼀个仿函数传给这个参数，实现这个仿函数的要求就是尽量key的每值都参与到计算中，让不同的key转换出的整形值不同。string做哈希表的key⾮常常⻅，所以我们可以考虑把string特化⼀下

template<class K>
struct HashFunc
{
   size_t operator()(const K& key)
   {
       return (size_t)key;
   }
};

// 哈希表中支持字符串的操作
template<>
struct HashFunc<string>
{
   size_t operator()(const string& key)
   {
       size_t hash = 0;
       for (auto e : key)
       {
           hash *= 31;
           hash += e;
       }

       return hash;
   }
};

2.4插入操作

插入的时候可能面临需要扩容的情况,所以需要判断负载因子后再进行插入,下面是插入的代码

bool Insert(const pair<K, V>& kv){if (Find(kv.first))//下面会实现查找功能return false;size_t size = _tables.size();if (_n * 10 / size >= 7)//判断当前储存的数据个数是否超过负载因子{size *= 2;HashTable<K,V> hs;hs._tables.resize(size);for (auto &e : _tables){if (e._state == EXIST)//存在才会从旧表迁移到新表hs.Insert(e._kv);}_tables.swap(hs._tables);}HashFunc<K> hf; size_t hashi = hf(kv.first) % size;while (_tables[hashi]._state == EXIST)//找到空或者被删除的地方{hashi++;}HashData<K, V> newdata;//插入节点并设置状态和增加数据个数newdata._kv = kv;newdata._state = EXIST;_tables[hashi] = newdata;_n++;return true;}

2.5查找操作

HashData<K, V>* Find(const K& key){HashFunc<K> hf;size_t size = _tables.size();size_t hashi = hf(key) % size;size_t hash0 = hashi;size_t i = 1;while (_tables[hashi]._state != EMPTY)//遍历哈希表{if (hf(_tables[hashi]._kv.first) == hf(key) && _tables[hashi]._state == EXIST)//数据存在且状态为存在return &_tables[hashi];hashi = (hash0 + i) % size;//超过size会从0继续遍历++i;}return nullptr;}

2.6删除操作

bool Erase(const K& key){HashData<K, V>* hd= Find(key);if (hd){hd->_state = DELETE;//将状态修改为删除--_n;return true;}return false;}

1.6.3 链地址法

解决冲突的思路

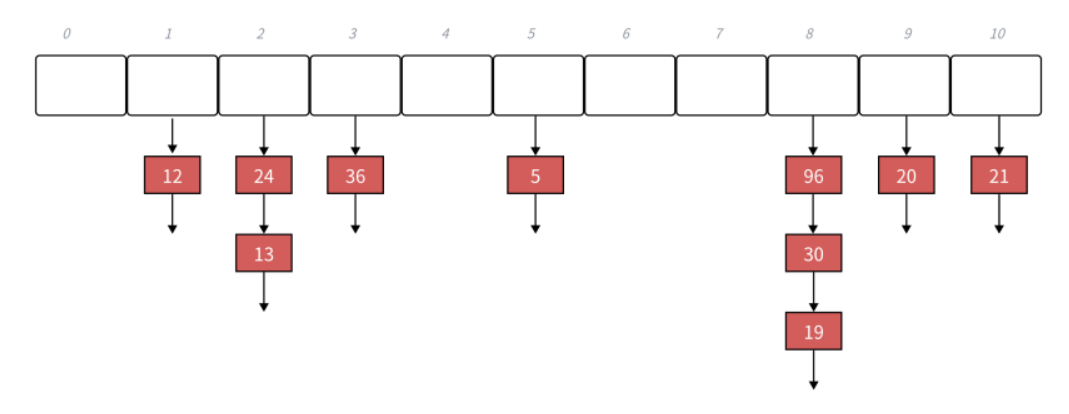
开放定址法中所有的元素都放到哈希表⾥，链地址法中所有的数据不再直接存储在哈希表中，哈希表中存储⼀个指针，没有数据映射这个位置时，这个指针为空，有多个数据映射到这个位置时，我们把这些冲突的数据链接成⼀个链表，挂在哈希表这个位置下⾯，链地址法也叫做拉链法或者哈希桶。

下⾯演⽰ {19,30,5,36,13,20,21,12,24,96} 等这⼀组值映射到M=11的表中。

3.1扩容

开放定址法负载因⼦必须⼩于1，链地址法的负载因⼦就没有限制了，可以⼤于1。负载因⼦越⼤，哈希冲突的概率越⾼，空间利⽤率越⾼；负载因⼦越⼩，哈希冲突的概率越低，空间利⽤率越低；stl中unordered_xxx的最⼤负载因⼦基本控制在1，⼤于1就扩容，我们下⾯实现也使⽤这个⽅式。

3.2代码实现

template<class T>struct HashNode{T _data;HashNode<T>* _next;HashNode(const T& data):_data(data), _next(nullptr){}};// K 为 T 中key的类型// T 可能是键值对，也可能是K// KeyOfT: 从T中提取key// Hash将key转化为整形，因为哈市函数使用除留余数法template<class K, class T, class KeyOfT, class Hash = HashFunc<K>>class HashTable{typedef HashNode<T> Node;public:HashTable(){_tables.resize(10, nullptr);}// 哈希桶的销毁/*~HashTable();*/// 插入值为data的元素，如果data存在则不插入bool Insert(const T& data){size_t size = _tables.size();KeyOfT kof;Hash hs;size_t key=kof(data);//将数据提取,如int 和pair<k,T>就需要使用不同的仿函数提取数据if (Find(key))return false;if (_n / size == 1){HashTable newHT;size_t newsize = 2 * size;newHT._tables.resize(newsize);for (int i = 0; i < size; i++){Node* cur = _tables[i];//遍历当前桶的数据while(cur){Node* next = cur->_next;cur->_next = nullptr;//旧表中节点，挪动新表重新映射的位置if (newHT._tables[hs(kof(cur->_data)) % newsize] == nullptr){newHT._tables[hs(kof(cur->_data)) % newsize] = cur;//如果是第一个映射的数据则直接插入}else{newHT._tables[hs(kof(cur->_data)) % newsize]->_next = cur;//不是第一个映射进行尾插}cur = next;}_tables[i] = nullptr;}_tables.swap(newHT._tables);//交换表}Node* newnode = new Node(data);//头插数据Node* prev = _tables[hs(kof(data) % size)];_tables[hs(kof(data) % size)] = newnode;newnode->_next = prev;_n++;return true;}// 在哈希桶中查找值为key的元素，存在返回true否则返回falsebool Find(const K& key){size_t size = _tables.size();KeyOfT kof;Hash hs;Node* node = _tables[hs(key) % size];//指定数据是哪一个桶while (node)//遍历当前桶{if (hs(kof(node->_data)) == hs(key)){return true;}node = node->_next;}return false;}// 哈希桶中删除key的元素，删除成功返回true，否则返回falsebool Erase(const K& key){size_t size = _tables.size();KeyOfT kof;Hash hs;Node* node = _tables[hs(key) % size];Node* prev = nullptr;while (node)//遍历数据所在桶{if (hs(kof(node->_data)) == hs(key))//找到改数据{if (prev){prev->_next = node->_next;delete node;--_n;return true;}else//如果是该桶第一个数据{if (node->_next)//后面有数据{_tables[hs(key) % size] = node->_next;}else//后面没有数据{_tables[hs(key) % size] = nullptr;}delete node;--_n;return true;}}prev = node;//保留前节点node = node->_next;//往下一个节点走}return false;}private:vector<Node*> _tables;  // 指针数组size_t _n = 0;			// 表中存储数据个数};

4.测试以上代码

void test1()
{open_address1::HashTable<int, int> h1;vector<pair<int, int>> v;v.push_back({ 1,1 });v.push_back({ 11,11 });v.push_back({ 2,2 });v.push_back({ 4,4 });v.push_back({ 6,6 });v.push_back({ 16,16 });v.push_back({ 8,8 });v.push_back({ 9,9 });for (auto e : v){h1.Insert(e);}h1.Insert({ 26,26 });h1.Insert({ 36,36 });if (h1.Find(1)){cout << "找到了" << endl;}elsecout << "没找到了" << endl;h1.Erase(1);if (h1.Find(1)){cout << "找到了" << endl;}elsecout << "没找到了" << endl;h1.Insert({ 41,41 });h1.Print();return;
}void test2()
{open_address1::HashTable<string, string> h2;h2.Insert({ "insert","插入" });h2.Insert({ "find","查找" });h2.Insert({ "aabb","aabb" });h2.Insert({ "bbaa","bbaa" });h2.Print();
}void test3()
{hash_bucket::HashTable<int,pair<int,int>, PairKeofT<int,int>> h1;vector<pair<int, int>> v;v.push_back({ 1,1 });v.push_back({ 11,11 });v.push_back({ 2,2 });v.push_back({ 4,4 });v.push_back({ 6,6 });v.push_back({ 16,16 });v.push_back({ 8,8 });v.push_back({ 9,9 });for (auto e : v){h1.Erase(e.first);}h1.Insert({ 26,26 });h1.Insert({ 36,36 });h1.Insert({ 46,46 });if(h1.Erase(46))cout<<"delete 46"<<endl;if (h1.Erase(36))cout << "delete 36"<<endl;if (h1.Erase(26))cout << "delete 26"<<endl;return;
}

4.1测试结果