当前位置：首页 > news >正文

交叉熵损失函数：从信息量、熵、KL散度出发的推导与理解

news 来源：原创 2025/4/26 11:53:56

哈喽，大家好我是我不是小upper。今天给大家从信息量、熵、KL散度出发的推导与理解方面去聊聊交叉熵损失函数。

本文将从单个事件的信息量定义出发，深入剖析系统熵、KL 散度（相对熵）以及交叉熵的关系和计算方法。

1 信息量

（1）信息量的基本思想

信息论的核心思想是，一个不太可能发生的事件一旦发生，其所提供的信息量要多于一个极有可能发生的事件。比如，“今天早上有日食” 相较于 “今天早上太阳升起了”，前者传达的信息量更为丰富。基于这样的基本思想，对信息进行量化需要满足以下三个重要性质：

非常可能发生的事件，其信息量相对较少。在极端情况下，必然会发生的事情，不具备任何信息量。
发生可能性较低的事件，具有更高的信息量。
独立事件的信息量具有可加性。举例来说，投掷硬币两次均正面向上所传递的信息量，应当是投掷一次硬币正面朝上信息量的两倍。

（2）信息量的定义与计算

为了满足上述三个性质，我们可以定义一个事件x的信息量为 $F(x)$ ，其具体的计算表达式为： $F(x) = - \log P(x)$ ，

其中 $P(x)$ 为事件x发生的概率。

信息量 $F(x)$ 的单位由对数函数的底数决定。当对数函数 $\log$ 的底数为e时，信息量 $F(x)$ 的单位是奈特（nats），一奈特是以 $1/e$ 的概率观测到一个事件时所获得的信息量。当对数函数 $\log$ 的底数为2时，信息量 $F(x)$ 的单位是比特（bit）或者香农（shannons）。

为何使用log函数？

首先，从对数函数的性质来看，当概率越小， $-\log P(x)$ 的值越大（因为对数前有负号）。这恰好与信息量的定义相契合，即越不可能发生的事件发生了，它所带来的信息量就越大。

其次，对数函数能够极大地简化多事件概率的乘法运算。在计算多个独立事件同时发生的概率时，对数函数可以将乘法运算转换为加法运算，从而显著降低计算的复杂度。例如，两个事件 $x_1$ 和 $x_2$ 同时发生的信息量为。

$F(x_1,x_2)=-\log(P(x_1)P(x_2)) = -\log P(x_1) -\log P(x_2)=F(x_1)+F(x_2)$

系数为何是 $-1$ ？

“一个发生概率很小的事件发生了” 相较于 “一个发生概率很大的事件发生了”，前者蕴含的信息量要更大。这清晰地表明，事件发生的概率与事件发生之后所带来的信息量成反比关系。然而，对数函数本身是单调递增的，为了使信息量满足 “概率越小，值越大” 这一特性，系数必须取-1，这样就能将对数函数转换为单调递减的形式。

（3）信息量的本质

简而言之，信息量可以被看作是一个事件从原来的不确定状态转变为确定状态时，难度究竟有多大。事件发生的概率越小，也就意味着其不确定性越高，事件发生的难度也就越高，那么事件发生之后所带来的信息量自然也就越大。

2 熵

（1）熵的概念

信息量主要衡量的是单个事件从原来的不确定变为确定的难度，而熵则是用来衡量整个系统从原来的不确定变为确定的难度。

（2）熵的计算方法探讨

假设存在两个系统（比如两场比赛的结果概率分布），如下所示。通过直观观察可以发现，系统 1 的不确定性明显大于系统 2（这里熵的单位与信息量一致，取决于对数底数，此处底数为 2）。

错误计算方式

如果直接计算系统中每个事件的信息量，然后将系统中所有事件的信息量相加作为系统整体的熵，最终得到的结果会与我们的预期明显相反（系统 1 中所有事件的信息量之和小于系统 2 中所有事件的信息量之和）。

正确计算方式

熵的正确计算方法应该是求系统中每个事件对系统贡献的信息量，也就是信息量的概率加权平均，这其实等同于求期望。

（3）熵的定义

根据上述分析，对于一个概率分布为P的系统，熵 $H(P)$ 可定义为： $H(P) = - \sum_{i = 1}^{m} P(x_i) \log P(x_i)$ 。该公式表示对系统中各个事件的信息量求期望，其中m为系统中事件的总数。

综上所述可以分析得出，对于一个概率分布为P的系统，熵H(P)可定义为：

（4）熵的意义

总的来说，熵能够有效地衡量系统整体的不确定程度（或者说混乱程度）。当系统的概率分布更接近确定性分布时，意味着系统的不确定性较低，此时熵的值也就越低；当系统的概率分布更接近均匀分布时，系统的不确定性较高，熵的值也就越高。

3 KL 散度（相对熵）

（1）KL 散度的定义与作用

KL 散度主要用于衡量两个系统（分布 / 概率模型）之间的差异。假设存在两个系统P和Q，两个系统中事件i的信息量可分别表示为 $-\log P(x_i)$ 和 $-\log Q(x_i)$ ，则 KL 散度可定义为：

$D_{KL}(P||Q) = \sum_{i = 1}^{m} P(x_i) [\log P(x_i) - \log Q(x_i)]$ 。

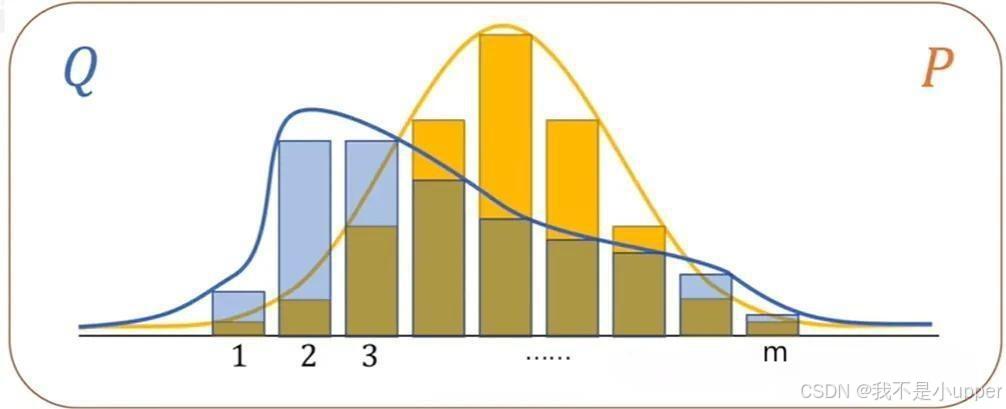
这个公式代表以P为基准，去计算P和Q的差异。具体来说， $\log P(x_i) - \log Q(x_i)$ 表示对于事件i，其在系统Q中的信息量减去在系统P中的信息量，最终对信息量的差异求整体的期望。

KL 散度的性质

KL 散度一定是大于等于0的，这一性质可以由吉布斯不等式证明。
根据上述公式推导结果可以看出，当事件i在两个系统中的发生概率 $P(x_i)$ 和 $Q(x_i)$ 相等时，最终结果为0。进一步地，当两个系统的分布完全一致时，KL 散度的结果为0，这表明两个系统之间不存在任何差异。反之，若结果不为0，则表示两个系统存在一定的差异。

（2）交叉熵的引出

从 KL 散度的推导结果中可以发现，公式第二项 $- \sum_{i = 1}^{m} P(x_i) \log P(x_i)$ 表示系统P的熵。由于系统P作为基准，其熵是恒定不变的。那么两个系统的差异是否趋近于0，仅仅取决于推导结果的第一项，该项即为交叉熵，可表示为

$H(P, Q) = - \sum_{i = 1}^{m} P(x_i) \log Q(x_i)$ 。

（3）KL 散度的非对称性

特别需要注意的是，KL 散度是非对称的，即对于P和Q， $D_{KL}(P||Q) \neq D_{KL}(Q||P)$ 。这意味着，选择P作为基准还是Q作为基准，对结果的影响是很大的。

在 $D_{KL}(P||Q)$ 中，以系统P作为基准，目标是衡量以分布Q近似真实分布P时所产生的信息损失。权重为 $P(x_i)$ 意味着， $P(x_i)$ 越大，对 KL 散度的贡献就越大，反之则越小。例如，若真实分布P为 $[0.7, 0.3]$ ，而近似分布Q为$[0.5, 0.5]$，则 KL 散度会更多地 “惩罚” 第一个事件的偏差，因为它在P中占比更高。

04 交叉熵

（1）交叉熵与系统分布的关系

根据上文的分析结果，如果要使两个系统（概率模型）的分布非常接近，那么就需要找到交叉熵的最小值（因为 KL 散度必定大于等于0，所以交叉熵越小，KL 散度就越趋近于0）。

（2）交叉熵在概率模型中的应用

在交叉熵 $H(P,Q)$ 中，系统P作为基准，可以将其理解为人脑模型（即标签），Q为概率模型。对于一个概率模型而言，我们便可以通过最小化交叉熵来衡量预测分布与真实分布之间的差异。

在 $H(P,Q)$ 的计算公式中， $P(x_i)$ 可代表真实标签， $Q(x_i)$ 可代表模型预测概率，m可表示样本数量。

接下来，我们可以将交叉熵推广到实际应用中的二分类问题和多分类问题中。

（3）二分类问题中的交叉熵损失函数

二分类问题中的交叉熵损失函数可定义为：

$L = - \frac{1}{N} \sum_{i = 1}^{N} [y_i \log p_i + (1 - y_i) \log (1 - p_i)]$ 。

在这个公式中， $y_i$ 代表样本i的标签， $p_i$ 代表模型预测结果（通过 sigmoid 函数输出），N为样本数量。

二分类问题的特点

在二分类问题中，输出层神经元数为1，直接输出正类概率p，负类概率为 $1-p$ 。输出层使用 sigmoid 函数，将输出压缩到 $(0,1)$ 区间，这样就能够表示正类概率。
对于每个样本，需要计算正类和负类的概率差异。例如，当真实标签为1时，仅计算正类预测误差（此时 $1 - y_i = 0$ ，第二项为0）；当真实标签为0时，仅计算负类预测误差（此时 $y_i = 0$ ，第一项为0）。

（4）多分类问题中的交叉熵损失函数

多分类问题中的交叉熵损失函数可定义为：

$L = - \frac{1}{N} \sum_{i = 1}^{N} \sum_{k = 1}^{K} y_{i,k} \log p_{i,k}$ 。

在这个公式中， $y_{i,k}$ 代表 one-hot 编码的标签， $p_{i,k}$ 代表模型预测结果，即样本属于第k类的概率（通过 softmax 函数输出），N为样本数量，K为类别数量。

多分类问题的特点

在多分类问题中，输出层神经元数量等于类别数K，每个神经元对应一个类别的概率。输出层使用 softmax 函数，确保所有类别概率之和为1。
仅计算真实类别对应的预测概率误差。例如，若真实类别为第k类，则只关注 $p_{i,k}$ ，其他类别的误差不计入损失（因为 $y_{i,k}$ 在真实类别处为1，其他位置为0）。