[计算机科学#3]：布尔逻辑 （计算机数学基础）
![[LOGO]:CoreKSets](https://i-blog.csdnimg.cn/direct/731088657ae348d4a1f679ad3008534a.png)
【核知坊】：释放青春想象，码动全新视野。
我们希望使用精简的信息传达知识的骨架，启发创造者开启创造之路！！！
内容摘要：本文详细介绍了计算机的核心数学基础-布尔逻辑学基础知识。详细说明了布尔逻辑基本三运算（AND,NOT,OR），以及使用电路图像展示了布尔逻辑在物理上的构造。
关键词：抽象 布尔逻辑
其他相关文章：
[计算机科学#1] 计算机的前世今生，从算盘到IBM的演变之路
https://blog.csdn.net/weixin_64094522/article/details/147463617
计算机科学#2]：从继电器到晶体管的电子计算机发展史（庞然大物的进化）https://blog.csdn.net/weixin_64094522/article/details/147538714
1.计算机抽象
计算机抽象是指通过隐藏底层复杂性，将复杂的系统分解为更简单、更易于理解和操作的层次的过程。每个抽象层次提供了一组简化的接口或功能，使得用户或开发者可以专注于当前层次的任务，而无需深入了解底层的具体实现细节。可以简单理解为将复杂事物简单化，将复杂逻辑包装起来一键调用，用户无需知道底层逻辑。
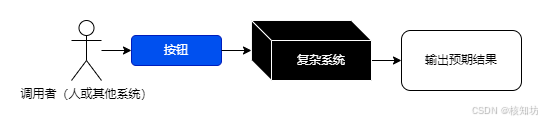
计算机系统通常可以分为多个抽象层次，每个层次都建立在下一层的基础上，同时为上一层提供服务。常见的抽象层次包括：
1.1 硬件层
-
晶体管和逻辑门：这是最底层的抽象，涉及物理硬件，如晶体管、逻辑门等。这些基本元件用于实现简单的逻辑操作（如AND、OR、NOT）。
-
电路和芯片：更高层次的硬件抽象，涉及集成电路和芯片设计。例如，CPU、内存等硬件组件。
1.2 操作系统层
-
系统调用和API：操作系统提供了系统调用和应用程序接口（API），隐藏了硬件的复杂性，使得程序可以更方便地访问硬件资源（如文件系统、内存管理、进程调度等）。
-
驱动程序：驱动程序是操作系统与硬件设备之间的桥梁，隐藏了硬件设备的具体操作细节。
1.3 编程语言层
-
高级编程语言：高级编程语言（如Python、Java、C++等）提供了更接近人类语言的语法和抽象，隐藏了底层的机器代码和硬件操作细节。
-
编译器和解释器：编译器和解释器将高级语言代码转换为机器代码，使得程序员可以使用高级语言编写程序，而无需直接编写机器代码。
1.4 软件应用层
-
库和框架：库和框架提供了更高级别的抽象，使得开发者可以更方便地实现复杂的任务，而无需从头开始编写所有代码。例如，Web开发框架（如Django、Flask）隐藏了底层的HTTP协议和网络操作细节。
-
用户界面：用户界面是最高层次的抽象，使得用户可以与计算机系统进行交互，而无需了解底层的实现细节。
1.5 抽象的意义
-
简化复杂性：通过隐藏底层细节，抽象使得系统更易于理解和管理。每个层次的用户只需要关注当前层次的功能，而无需了解底层的具体实现。
-
提高效率：抽象允许开发者和用户在更高的层次上工作，从而提高开发效率和系统的运行效率。
-
模块化和重用：抽象使得系统可以被分解为独立的模块，这些模块可以在不同的系统中重用，从而提高系统的可维护性和可扩展性。
-
降低错误率：通过隐藏底层的复杂性，抽象减少了出错的可能性，使得系统更加稳定和可靠。
2.计算机为什么使用二进制？
2.1 十进制（Decimal）
十进制是我们日常生活中最常用的数制，它基于10个数字（0到9）。每个数字的位置代表10的幂次。例如，数字123可以表示为：
1×10^2+2×10^1+3×10^0=100+20+3=123
-
个位：代表 10^0（即1）
-
十位：代表10^1（即10）
-
百位：代表 10^2（即100）
-
.......
2.2 二进制（Binary）
二进制是一种基于2的数制，它只有两个数字：0和1。每个数字的位置代表2的幂次。例如，二进制数101可以表示为：
1×2^2+0×2^1+1×2^0=4+0+1=5(十进制)
个位：代表 2^0（即1）
-
二位：代表 2^1（即2）
-
四位：代表 2^2（即4）
-
......
2.3 从十进制到二进制的转换
将十进制数转换为二进制数的过程是通过不断地除以2，并记录余数来完成的。例如，将十进制数13转换为二进制：
将余数从下到上依次排列，得到二进制数1101。
2.4 二进制的优势
二进制类似于太极中的阴阳，这种对立关系不仅清晰明了，而且在物理实现和逻辑处理中都具有显著的优势。二进制可以表示2个状态，10进制10个状态，在信号干扰的情况下，明显状态越多越难管理和控制，并且状态越多，计算机底层单元越复杂，越复杂的东西故障率往往越高，不可靠。
-
电子元件的两种状态：在电子电路中，很容易实现两种状态：有电流（1）和无电流（0）。这种简单的开/关状态非常适合用二进制表示。
-
稳定性和可靠性：二进制的两种状态之间有明显的区别，减少了信号干扰和错误的可能性。例如，如果电路中有噪声，只要信号强度足够，仍然可以准确区分0和1。
-
简单的存储单元：二进制的0和1可以用简单的存储单元（如晶体管）来存储，每个存储单元只需要区分两种状态。
-
高效的计算：二进制的加法、减法、乘法和除法等运算规则简单，计算机可以高效地实现这些运算。
3.什么是布尔逻辑？
布尔逻辑（Boolean Logic）是一种数学逻辑，由乔治·布尔（George Boole）在19世纪中叶提出。它基于布尔代数，使用二元值（0和1，或true和false）来表示和处理信息。布尔逻辑是现代计算机科学和数字电子学的基石，因为它为计算机处理和存储信息提供了一种简单而强大的方法。
布尔逻辑不仅是一种数学工具，它还反映了我们对世界的理解和描述。在哲学上，布尔逻辑的二元性（true和false）与对立统一的辩证法相呼应。它提供了一种简化复杂问题的方法，通过将问题分解为基本的二元选择，我们可以更清晰地分析和解决这些问题。
在现实世界中，布尔逻辑的应用无处不在。从简单的开关电路到复杂的计算机系统，布尔逻辑都是其设计和运行的基础。它使我们能够以一种精确和可预测的方式处理信息，这是现代科技和工业发展的关键。
4.布尔代数的基本操作
与（AND）、非（NOT）和或（OR）是基本的逻辑运算，它们可以组合起来实现任何复杂的逻辑运算。因此，它们被称为逻辑运算的“原子式”。true == 1; false == 0
4.1NOT(非)操作
NOT操作是一个单输入操作，它将输入值反转。如果输入是true，输出是false；如果输入是false，输出是true。
| 输入 (A) | 输出 (NOT A) |
|---|---|
| true | false |
| false | true |
4.2AND(与)操作
AND操作有两个输入和一个输出。只有当两个输入都是true时，输出才是true。否则，输出是false。
| 输入 A | 输入 B | 输出 (A AND B) |
|---|---|---|
| true | true | true |
| true | false | false |
| false | true | false |
| false | false | false |
4.3OR(或)操作
OR操作也有两个输入和一个输出。只要有一个输入是true，输出就是true。只有当两个输入都是false时，输出才是false。
| 输入 A | 输入 B | 输出 (A OR B) |
|---|---|---|
| true | true | true |
| true | false | true |
| false | true | true |
| false | false | false |
5.硬件如何实现逻辑门
晶体管可以作为开关，控制电流的流动。通过控制线的通电状态，可以决定电流是否通过晶体管。
5.1NOT门 
(!)
通过将输出线放在晶体管之前，实现NOT操作。当输入为true时，电流被引导到地，输出为false；当输入为false时，电流通过输出线，输出为true。
5.2AND门
( & )
通过串联两个晶体管实现AND操作。只有当两个晶体管都导通时，电流才能通过，输出为true。
5.3OR门
(|)
通过并联两个晶体管实现OR操作。只要有一个晶体管导通，电流就可以通过，输出为true。
6.XOR （异或操作）
XOR（异或）操作类似于OR操作，但当两个输入都为true时，输出为false。只有当一个输入为true而另一个为false时，输出才为true。XOR门可以通过组合NOT、AND和OR门来实现。它在计算机科学中非常有用，例如在数据校验和加密中。
| 输入 A | 输入 B | 输出 (A XOR B) |
|---|---|---|
| true | true | false |
| true | false | true |
| false | true | true |
| false | false | false |
7.生活中的布尔逻辑
（1）日常决策
-
如果天气好（
Weather）并且你有空闲时间（FreeTime），那么你去散步。 -
如果天气不好或者你没有空闲时间，那么你不去散步。
（2）购物决策
-
如果商品价格合理（
Price）并且你有需求（Need），那么你购买。 -
如果价格不合理或者你没有需求，那么你不购买。
（3）交通信号灯
-
如果是绿灯（
GreenLight），你可以通过路口。 -
如果是红灯（
RedLight），你必须停止。 -
如果是黄灯（
YellowLight），你可以减速通过。
（4）家庭自动化
-
如果是晚上（
Night）并且房间内有人（Presence），灯会打开。 -
如果是白天或者房间内没有人，灯会关闭。
（5）健康监测
-
如果体温正常（
NormalTemperature）并且没有咳嗽（NoCough），那么你认为自己健康。 -
如果体温异常或者有咳嗽，那么你认为自己可能生病了。
（6）时间管理
-
如果你有足够的时间（
EnoughTime）并且项目有趣（Interesting），那么你开始新的项目。 -
如果你没有足够的时间或者项目不有趣，那么你暂时搁置。
文章总结
本文通过介绍布尔逻辑和逻辑门，展示了计算机如何通过简单的二进制状态来实现复杂的逻辑功能。
感谢阅览，如果你喜欢该内容的话，可以点赞，收藏，转发。由于 Koro 能力有限，有任何问题请在评论区内提出，Koro 看到后第一时间回复您！！！