[论文梳理] 足式机器人规划控制流程 - 接触碰撞的控制 - 模型误差 - 自动驾驶车的安全合规(4个课堂讨论问题)
目录
问题 1:足式机器人运动规划 & 控制的典型流程 (pipline)
1.1 问题
1.2 目标
1.3 典型流程(Pipeline)
1.3.1 环境感知(Perception)
1.3.2 高层规划(High-Level Planning)
1.3.3 足迹规划(Footstep Planning)
1.3.4 身体轨迹生成(Body Trajectory Generation / Trajectory Optimization)
补充论文
1.3.5 全身控制(Whole-Body Control, WBC)
1.3.6 反馈闭环
问题 2:接触事件建模 & 混合系统控制
2.1 问题
2.2 背景
2.3 接触建模方法
2.4 混合系统控制方法
问题 3:处理模型误差
3.1 问题
3.2 背景
3.3 处理方法
问题 4:自动驾驶汽车的安全交互 & 驾驶模式差异
4.1 问题
4.2 意外交互中的安全 & 合规
4.3 普通驾驶 vs. 赛车 的区别
- 港科广 马老师 的机器人学 课堂讨论 (seminar) 记录
- 问题驱动的学习,有助于进一步提出有价值的问题
- 梳理机器人运动规划和控制领域的主流问题和技术
- 以问题为框架,梳理论文更高效
问题 1:足式机器人运动规划 & 控制的典型流程 (pipline)
1.1 问题
足式机器人 因其在复杂地形中的高机动性而备受关注。那么,足式机器人的 运动规划与控制 的 典型流程(pipeline)是怎样的?
1.2 目标
- 使足式机器人在复杂环境中稳定、高效地移动
1.3 典型流程(Pipeline)
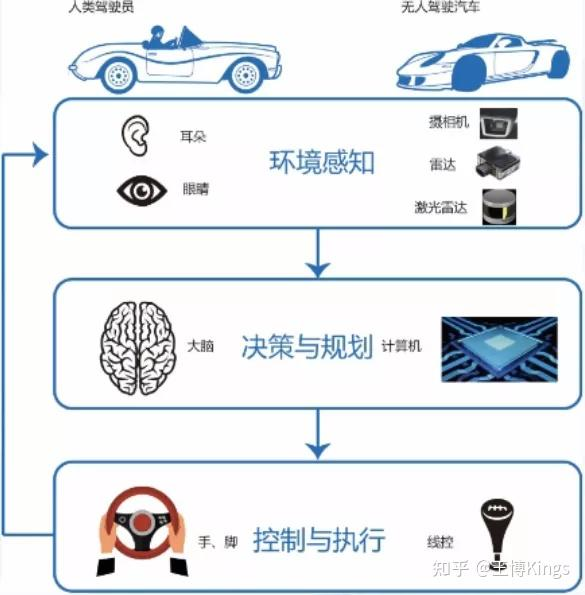
1.3.1 环境感知(Perception)
- 使用传感器(激光雷达 LiDAR、摄像头 Camera、惯性测量单元 IMU、关节编码器、足底力传感器等)获取环境信息(地形、障碍物)和机器人自身状态(位置、姿态、速度、接触状态)
- 生成环境地图(如点云图、栅格图、高程图)和估计机器人状态(State Estimation)。状态估计通常融合 IMU、运动学和接触信息

1.3.2 高层规划(High-Level Planning)
- 根据任务目标(如“到达 A 点”)和环境地图,规划出一条全局路径(通常是机器人身体中心 质心 (CoM) [质量中心] 的路径),避开大的障碍物。常用算法如图搜索(A*, RRT*)
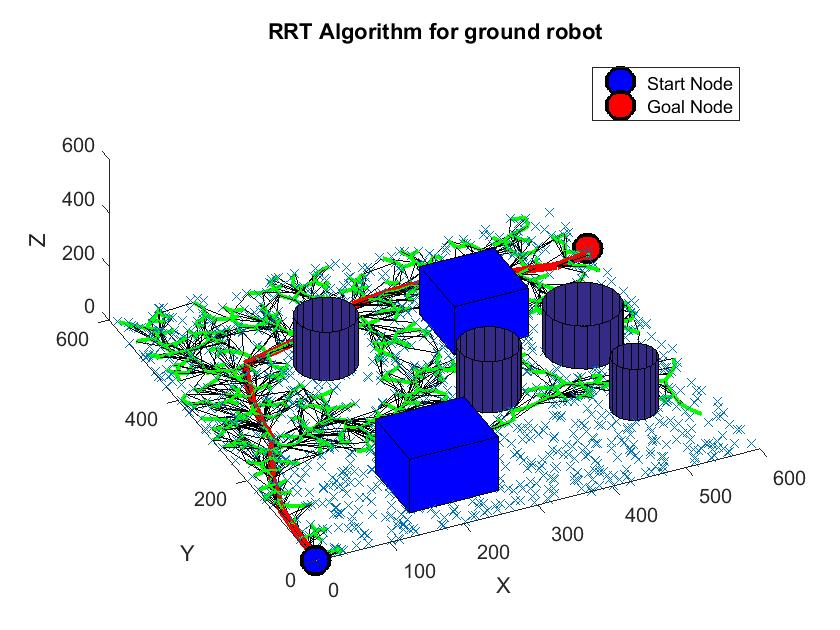

- 最新的接入LLM的高层规划导航方法有:

AAAI-2024 | 视觉语言导航-NavGPT: [2305.16986] NavGPT: Explicit Reasoning in Vision-and-Language Navigation with Large Language Models (arxiv.org)
1.3.3 足迹规划(Footstep Planning)
- 根据高层规划的路径和局部地形信息,规划出一系列离散的足底落点位置和时间。
- 需要考虑:运动学可达性(腿长限制)、运动稳定性(如基于 ZMP - Zero Moment Point、Capture Point 的判据)、地形适应性(寻找平坦、稳固的落脚点)、避免碰撞等

1.3.4 身体轨迹生成(Body Trajectory Generation / Trajectory Optimization)
- 根据规划好的足迹,生成机器人身体(CoM)和摆动腿(Swing Leg)的连续运动轨迹
- 通常是一个优化问题,目标是平滑、节能、稳定,同时满足动力学约束(如 ZMP 约束)、运动学约束和足迹约束
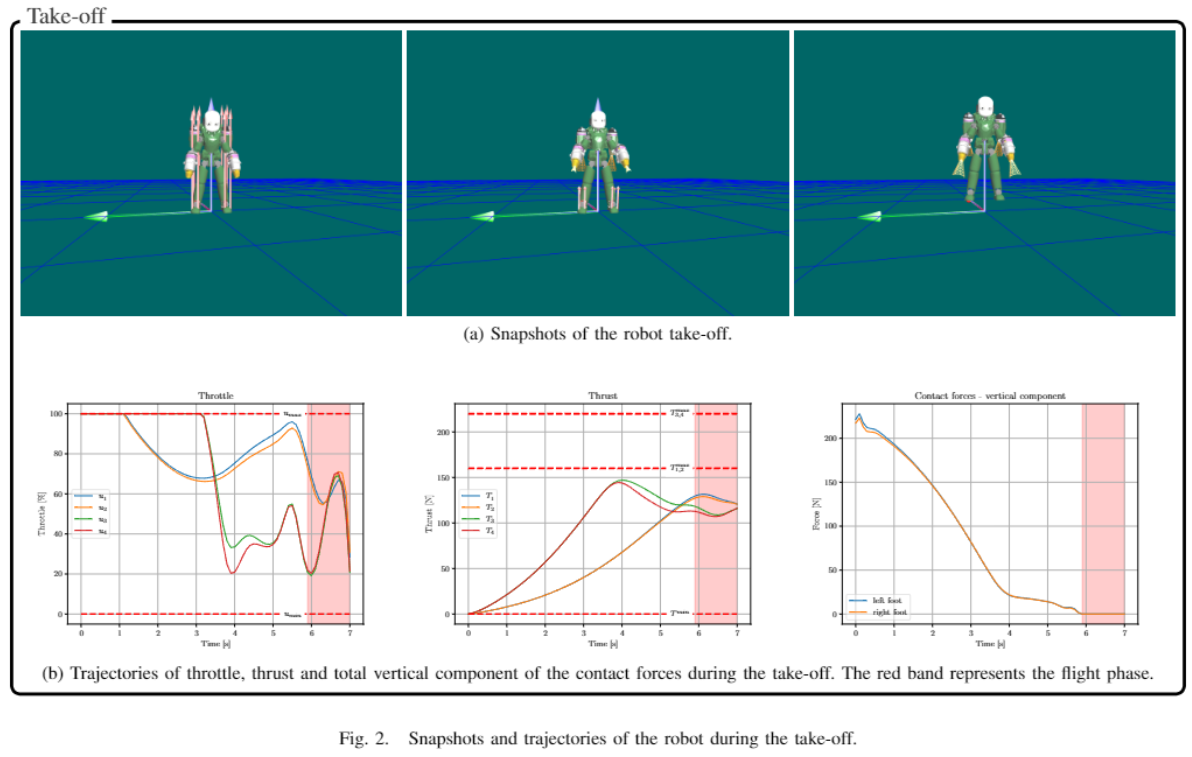
补充论文
- 其它的轨迹生成的工作(不是全身轨迹,只是手臂轨迹生成)

ICL伦敦帝国理工-2023年的工作: [2309.07550] Naturalistic Robot Arm Trajectory Generation via Representation Learning (arxiv.org)
- 最新的接入LLM的端到端视觉-语言-动作模型有:(直接从感知 -> 动作轨迹生成)

Google 2023年的 RT-2 的端到端训练:在机器人和公开数据上共同微调了一个预训练的视觉-语言模型(VLM)。得到的模型接收机器人摄像头图像,语言指令,当前动作,并直接预测机器人执行的动作 
类似于LLaVA用transformer做next token prediction;输入:视觉token+文本token+先前动作token;输出:动作token (做下一步的规划控制)
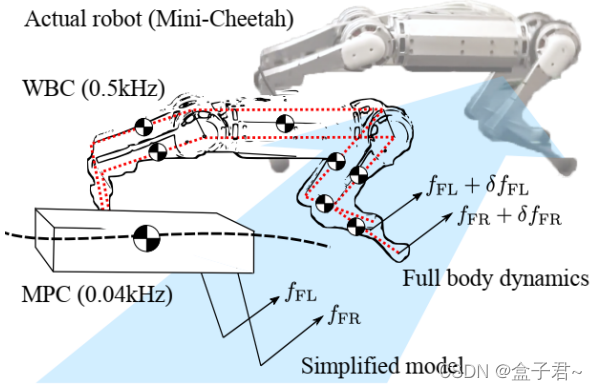
1.3.5 全身控制(Whole-Body Control, WBC)
- 这是最底层的控制。根据期望的身体轨迹、足部轨迹和接触状态,计算需要施加到每个关节的力矩(Torque)
- 通常也表述为一个优化问题(如二次规划 QP),目标是精确跟踪期望运动,同时满足多个任务和约束:
- 任务(优先级可能不同): 保持身体姿态、跟踪 CoM 轨迹、跟踪摆动腿轨迹、维持接触力等。
- 约束: 关节角度/速度/力矩限制、摩擦力约束(Friction Cone)、接触运动学约束(着地脚速度为零)
- 常用方法包括基于任务空间/操作空间(Task/Operational Space)的控制、基于逆动力学的控制等。
1.3.6 反馈闭环
- 整个流程是闭环的。感知到的实际状态会反馈给规划和控制层,用于纠正偏差
- 例如,如果实际落脚点与计划不符,或身体姿态发生倾斜,控制器会实时调整
问题 2:接触事件建模 & 混合系统控制
2.1 问题
接触事件 会导致系统状态发生不连续的跳变(例如速度突变)。我们如何有效地在 系统动力学 中为这种接触进行 建模?对于这类具有 非光滑动力学 特性的 混合系统(hybrid systems),我们又该如何进行 控制?
2.2 背景
- 接触(如机器人脚落地、物体碰撞)是许多物理系统中常见的现象。它会导致速度、加速度等状态量瞬间改变,使得系统的动力学模型在接触点变得不连续、非光滑。这类系统既包含连续变化的动态(如空中飞行),又包含离散的事件(接触瞬间),因此被称为“混合系统”
2.3 接触建模方法
- 刚体碰撞模型(Impact Maps): 这是最经典的方法之一。假设碰撞时间无限短,利用冲量-动量定理来计算碰撞后的速度。通常会引入“恢复系数”(Coefficient of Restitution, e)来描述碰撞的能量损失程度(e=1 为完全弹性碰撞, e=0 为完全非弹性碰撞)。对于多点接触或复杂几何体,需要考虑接触点的位置、法线方向以及摩擦(如库仑摩擦模型)
- 连续接触力模型(Penalty Methods / Regularization): 这种方法避免了不连续性。它将接触力模拟为非常“硬”的弹簧和阻尼器。当物体相互穿透时,会产生一个非常大的排斥力将它们推开。优点是模型是连续的,易于仿真和控制设计;缺点是需要选择合适的刚度和阻尼系数,可能导致数值计算上的“刚性问题”(stiffness),并且物理真实性可能不如碰撞模型
- 互补约束(Complementarity Constraints): 这是目前在机器人学和仿真中非常流行且物理意义明确的方法。它将接触条件(如:不穿透距离 d≥0、接触力 fn≥0、两者不能同时大于零 d⋅fn=0)以及摩擦力(如最大静摩擦力约束)表示为一组数学上的互补约束(通常是线性互补问题 LCP 或非线性互补问题 NCP)。这种方法能够精确地描述“接触/分离”的逻辑切换
- 事件驱动方法(Event-Driven): 精确地检测接触事件发生的时间点,然后在事件点切换动力学模型或应用冲击模型。这在仿真中很常用,但在实时控制中可能较难实现
2.4 混合系统控制方法
- 分段控制/切换系统理论(Switched Systems): 为系统的每种模态(接触/非接触)分别设计控制器,并设计切换逻辑来保证稳定性。挑战在于处理切换瞬间的状态跳变和保证切换过程的稳定性
- 模型预测控制(MPC): MPC 天然适合处理约束。可以将互补约束或接触力约束直接纳入优化问题中,预测未来一段时间的系统行为并计算最优控制输入。对于混合系统,需要使用混合整数规划(Mixed-Integer Programming)或专门处理互补约束的优化算法
- 能量/耗散理论(Passivity-Based Control): 利用系统的能量特性来设计控制器,特别是在处理接触时的能量交换和耗散
- 力/阻抗控制(Force/Impedance Control): 不直接控制位置,而是控制机器人与环境交互时的力或表现出的机械阻抗(力与位移/速度的关系)。这对于处理接触时的不确定性和保证柔顺性非常有效。
- 基于学习的控制: 利用强化学习等方法让系统自主学习如何在接触中稳定运动
问题 3:处理模型误差
3.1 问题
模型 总归是 近似 的。我们如何处理模型中存在的 误差?
3.2 背景
- 任何数学模型都是对现实世界的简化和近似。误差来源包括:参数不确定(质量、摩擦系数未知)、未建模的动态(如柔性、驱动器延迟)、传感器噪声、环境干扰等
3.3 处理方法
- 鲁棒控制(Robust Control): 设计控制器时就考虑模型不确定性的存在范围,目标是即使在最坏的模型误差情况下,系统依然能保持稳定并满足一定的性能指标。常用方法包括 H-infinity 控制、滑模控制(Sliding Mode Control)等。滑模控制对匹配不确定性(matching uncertainty)尤其鲁棒
- 自适应控制(Adaptive Control): 控制器能够在线估计模型参数或不确定性的大小,并根据估计结果调整自身的控制律,以适应模型变化
- 迭代学习控制(Iterative Learning Control, ILC): 适用于重复性任务。通过每次试验的误差来修正下一次试验的控制输入,逐步提高性能,对模型精度要求不高
- 基于观测器的控制: 设计状态观测器(如卡尔曼滤波器、扩展卡尔曼滤波器、无迹卡尔曼滤波器、粒子滤波器等)来估计系统内部状态和干扰,并将估计值用于反馈控制,以补偿模型误差和噪声的影响
- 数据驱动/学习方法:
- 系统辨识(System Identification): 在控制设计前,通过实验数据更精确地估计模型参数或建立数据驱动模型
- 残差建模(Residual Modeling): 用机器学习模型(如高斯过程、神经网络)来学习“标称模型”(nominal model)与实际系统之间的差异(残差),并将这个学习到的残差加入到控制设计中
- 强化学习(Reinforcement Learning): 直接从与环境的交互中学习最优控制策略,可以不依赖精确的模型
- 增加反馈增益: 在一定范围内,提高反馈控制器的增益可以增强系统抑制干扰和克服模型误差的能力,但过高的增益可能导致系统不稳定或放大噪声
问题 4:自动驾驶汽车的安全交互 & 驾驶模式差异
4.1 问题
自动驾驶汽车 有时需要进行 激进驾驶(aggressive driving)并与其它车辆进行复杂的 交互。在这种 意外交互 发生时,我们如何保证车辆行为的 安全 和 合规(compliant)?此外,普通驾驶 和 赛车(car racing)之间有什么 区别?
4.2 意外交互中的安全 & 合规
- 环境感知与预测: 精确感知周围车辆、行人、障碍物的位置、速度和意图。利用运动模型、交互模型甚至机器学习模型预测它们未来的行为轨迹
- 风险评估: 实时评估潜在的碰撞风险(如 Time-to-Collision, TTC)和其他危险情况
- 决策规划:
- 规则遵从: 严格遵守交通规则(如保持车道、安全距离、让行规则)。形式化方法(如 RSS - Responsibility-Sensitive Safety)可以提供可验证的安全保证
- 防御性驾驶策略: 预留足够的安全裕度,对其他道路使用者的不确定行为保持警惕,选择风险最低的策略
- 应急处理(Contingency Planning): 预先设计好应对突发危险情况(如前方急刹、鬼探头)的紧急避险策略(紧急制动、紧急变道),并能在极短时间内触发执行
- 运动控制: 精确、平稳地执行规划出的轨迹,同时具备快速响应能力以执行紧急操作
- 冗余与容错: 在传感器、计算单元、执行器等关键部件上采用冗余设计,确保单一故障不会导致灾难性后果
- V2X 通信(Vehicle-to-Everything): 与其他车辆、基础设施通信,提前获取危险警告或意图信息,有助于协同决策,但不能完全依赖
4.3 普通驾驶 vs. 赛车 的区别
- 目标(Objective):
- 普通驾驶:安全、舒适、高效(节能、省时)、遵守交通规则是首要目标
- 赛车:唯一目标是最小化单圈时间。在规则允许范围内,将车辆性能发挥到极限
- 运行环境(Environment):
- 普通驾驶:开放道路,环境复杂多变,充满不确定性(其他车辆、行人、信号灯、天气等)。需要遵守统一的交通法规
- 赛车:封闭赛道,环境相对可控,对手是专业的赛车手(行为更激进但也相对可预测),有特定的比赛规则
- 车辆极限(Vehicle Limits):
- 普通驾驶:通常在车辆的远低于极限的范围内运行,追求平稳和舒适
- 赛车:持续在车辆的物理极限(轮胎抓地力、发动机功率、刹车性能)边缘驾驶
- 驾驶策略(Strategy):
- 普通驾驶:保持车道、平稳加减速、保持安全距离
- 赛车:寻找最优“赛车线”(Racing Line),最大化利用赛道宽度,进行极限刹车、最大加速度出弯,容忍甚至利用轮胎的小幅滑移(Slip Angle)
- 风险容忍度(Risk Tolerance):
- 普通驾驶:极低,以避免任何事故为目标
- 赛车:较高,为了追求速度,可以接受一定的失控风险(如打滑、冲出赛道)
- 控制算法侧重:
- 普通驾驶:侧重安全性(碰撞避免)、平顺性、规则遵守、能耗优化
- 赛车:侧重极限性能下的轨迹跟踪、状态估计(如轮胎滑移率)、最优控制(如最小时间 MPC)
