leetcode--盛最多水的容器，接雨水

11.盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

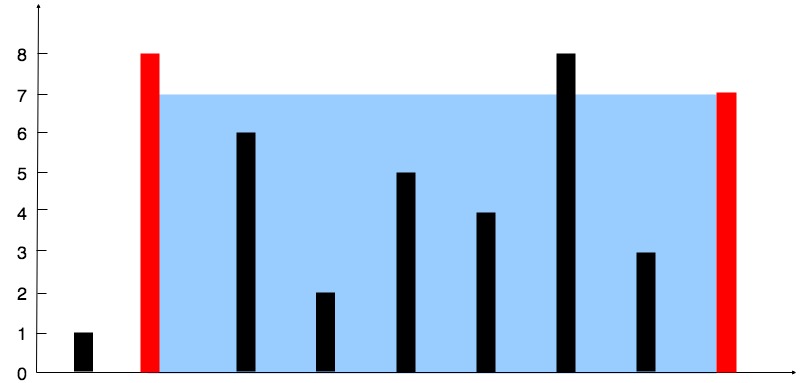
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1提示：

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

题解：

随便选择两条线，那么容纳的水量就是这块蓝色的面积。接着，看右边这条更短的线，它和中间的线构成容器的话，我们可以分类讨论一下：

（1）如果中间的线比它短，那么容纳的水宽度变短，高度变小，则这一部分的面积肯定比蓝色部分的面积小

（2）如果中间的线一样长，或者比它长，那么容纳水的高度不变，宽度变小，则这一部分的面积仍然比蓝色部分的面积小

因此中间的任何线都无法与它构成容量更大的容器了。换句话说，如果要找到一个容量比蓝色区域部分更大的容器，那么肯定不会包含这条线（如 ，右边这条红色的线），所以可以直接去掉，在剩下的线中继续去找

  既然这样，那我们可以初始化两个指针，left-0,right=n-1,哪条线短就移动哪条，如果一样长，移动两个的任意一个即可。在移动之前，先把所围成的面积算出来，如果比答案大，就更新答案

时间复杂度为O(N)

空间复杂度为O(1)

class Solution {
public:int maxArea(vector<int>& height) {int ans=0;int n=height.size();int area;//存储最大水量//相向双指针的用法int left=0;int right=n-1;while(left<right){area=min(height[right],height[left])*(right-left);ans=max(area,ans);if(height[left]<height[right])left+=1;elseright-=1;}return ans;}
};

42.接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[i] <= 105

题解：

       对于接雨水， 对于某一竖列i看它能接多少水， 就看它左侧的最大墙壁高度以及右侧的最大墙壁高度。

      如果所有左侧墙壁最大高度或者右侧墙壁最大高度都低于当前竖列i的情况下， 这一竖列不可能接到水， 因为会从它左侧或者右侧流出，只有当左侧出现有高于当前墙壁以及右侧也高于当前墙壁时，才可以接到水。

       竖列i接到的水=左右侧最低的那面墙-当前i墙壁的高度，然后对每一个竖列墙壁都这么计算

class Solution {
public:int trap(vector<int>& height) {int ans=0;int left=0;int right=height.size()-1;int pre_max=0;//前缀和int suf_max=0;//后缀和while(left<right){pre_max=max(pre_max,height[left]);suf_max=max(suf_max,height[right]);ans+=pre_max<suf_max?pre_max-height[left++]:suf_max-height[right--];}return ans;}
};