从线性回归到逻辑回归

逻辑回归简介

• 逻辑回归算法是基于多元线性回归的算法，逻辑回归是一个分类的算法，逻辑回归算法是基于多元线性回归的算法。
• 逻辑回归是线性的分类器。
• 拓展：基于决策树的一系列算法，基于神经网络的算法等那些是非线性的算法。SVM支持向量机的本质是线性的，但是也可以通过内部的核函数升维来变成非线性的算法。

sigmoid函数绘制

import mathimport matplotlib.pyplot as plt
import numpydef sigmoid(x):a=[]for item in x:a.append(1.0/(1.0+math.exp(-item)))return ax=numpy.arange(-10,10,0.1)
y=sigmoid(x)plt.title("sigmoid function achieve")
plt.plot(x,y)
plt.xlabel("x")
plt.ylabel("y")plt.show()

Sigmoid 作用

• 逻辑回归就是在多元线性回归基础上把结果缩放到0到1之间。$h_{\theta }(x)$越接近+1越是正例， $h_{\theta }(x)$越接近0越是负例，根据中间0.5分为二类。
  $$h_{\theta }(x)=g({\theta }^{T}x)=\frac{1}{1+e^{-{\theta }^{T}x}}$$
• 分类器的本质就是要找到分界，当把0.5作为分界时，即$z={\theta }^{T}x=0$的解
  

逻辑回归使用sigmoid函数的原因

Sigmoid函数天然满足：

1. 概率映射（输出∈(0,1)）
2. 对数几率线性化
3. 与伯努利分布完美结合
   因此成为逻辑回归的理想选择。

---

• 核心原因：
  Sigmoid函数能将线性模型的输出（任意实数）压缩到(0,1)区间，直接对应“属于正类的概率”，同时满足二分类中“正负类概率之和为1”的要求。

关键推导步骤

1. 建模概率比值：
   假设正类概率为$P(y=1)=p$，负类概率$P(y=0)=1-p$。定义**几率比（Odds Ratio）**为：
   $$\text{Odds}=\frac{p}{1-p}$$
   取对数后，用线性模型拟合：
   $$\log \left(\frac{p}{1-p}\right)=w^{T}x+b$$

2. 解出概率$p$
   通过指数运算反解：
   $$\frac{p}{1-p}=e^{w^{T}x+b}⟹p=\frac{e^{w^{T}x+b}}{1+e^{w^{T}x+b}}=\frac{1}{1+e^{-(w^{T}x+b)}}$$
   最终形式正是Sigmoid函数：
   $$P(y=1)=\sigma (w^{T}x+b)=\frac{1}{1+e^{-(w^{T}x+b)}}$$

伯努利分布关联

逻辑回归的标签 ( y ) 服从伯努利分布（ y ∈ { 0 , 1 } y \in \{0,1\} y∈{0,1}），其概率质量函数可统一写成：
$$P(y)=p^y(1-p{)}^{1-y},\text{其中}p=\sigma (w^{T}x+b)$$
最大化该分布的似然函数，即得到逻辑回归的优化目标。

广义线性模型和指数族分布

• 从伯努利分布到Sigmoid：广义线性模型的核心推导和线性回归的指数族统一视角：从高斯分布到最小二乘法

逻辑回归损失函数的推导

• 根据若干已知的X,y（训练集）找到一组W使得X作为已知条件下y发生的概率最大。逻辑回归中既然$g(w,x)$的输出含义为$P(y=1|w,x)$，那么$P(y=0|w,x)=1-g(w,x)$。
  
  $$p(y|x:\theta )=(h_{\theta }(x){)}^y(1-h_{\theta }(x){)}^{1-y}$$

$$\begin{array}{rl}L(\theta )& =p(\vec{y}|X;\theta )\\ & =\prod _{i=1}^{m}p(y^{(i)}|x^{(i)};\theta )\\ & =\prod _{i=1}^m{\left(h_{\theta }(x^{(i)})\right)}^{y^{(i)}}{\left(1-h_{\theta }(x^{(i)})\right)}^{1-y^{(i)}}\end{array}$$

1. 符号对齐：

   • $h_{\theta }(x^{(i)})$ 表示样本 $x^{(i)}$ 的预测概率 $\sigma ({\theta }^{T}x)$
   • 指数部分 $y^{(i)}$ 和 $1-y^{(i)}$ 构成伯努利分布的紧凑表达式

2. 推导逻辑：
   $$\begin{array}{rl}\text{当 }{y}^{(i)}=1& :h_{\theta }(x^{(i)}{)}^1\cdot (1-h_{\theta }(x^{(i)}){)}^0=h_{\theta }(x^{(i)})\\ \text{当 }{y}^{(i)}=0& :h_{\theta }(x^{(i)}{)}^0\cdot (1-h_{\theta }(x^{(i)}){)}^1=1-h_{\theta }(x^{(i)})\end{array}$$

3. 对数似然转换：
   $$\begin{array}{rl}\ell (\theta )& =\log L(\theta )\\ & =\sum _{i=1}^m\left[y^{(i)}\log h_{\theta }(x^{(i)})+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))\right]\end{array}$$

4. 最终形式：损失函数，往往是求最小，可以用梯度下降来求解。最终损失函数就是上面公式加负号的形式：
   $$\begin{array}{rl}\ell (\theta )& =-\sum _{i=1}^m\left[y^{(i)}\log h_{\theta }(x^{(i)})+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))\right]\end{array}$$

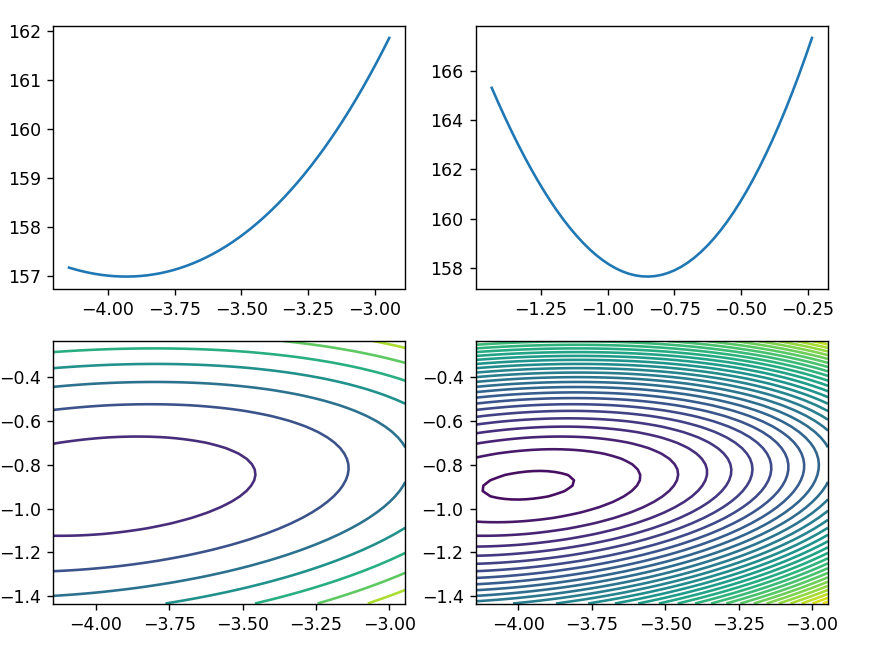
绘制损失函数

from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.preprocessing import scale# 加载数据集并进行归一化处理
data = load_breast_cancer()
# 提取数据集中前两个特征作为x，并将目标值作为y
x, y = scale(data['data'][:, :2]), data['target']
# 使用逻辑回归算法求解两个特征对应的最优参数
# 设置fit_intercept=False，因为逻辑回归模型本身已经包含了截距项，无需额外计算
lr = LogisticRegression(fit_intercept=False)
lr.fit(x, y)
# 提取逻辑回归模型中两个特征对应的权重参数W1和W2
theta1 = lr.coef_[0, 0]
theta2 = lr.coef_[0, 1]
# 打印提取的权重参数W1和W2
print(theta1, theta2)# 定义函数p_theta_function，用于计算给定特征和权重时的预测概率
def p_theta_function(features, w1, w2):# 计算线性组合z = w1 * x1 + w2 * x2z = w1 * features[0] + w2 * features[1]# 使用sigmoid函数将z转换为概率值return 1 / (1 + np.exp(-z))# 定义函数loss_function，用于计算给定权重W1和W2时的数据集损失
def loss_function(samples_features, samples_labels, w1, w2):result = 0# 遍历数据集中的每个样本，计算总体损失for features, label in zip(samples_features, samples_labels):# 调用p_theta_function计算当前样本的预测概率p_result = p_theta_function(features, w1, w2)# 根据交叉熵损失公式计算当前样本的损失loss_result = -1 * label * np.log(p_result) - (1 - label) * np.log(1 - p_result)result += loss_result# 返回结果（此处代码存在逻辑问题，应在遍历结束后统一返回）return result# 创建运维数组，平均取值50个点
theta1_space = np.linspace(theta1 - 0.6, theta1 + 0.6, 50)
theta2_space = np.linspace(theta2 - 0.6, theta2 + 0.6, 50)# 计算在不同theta1和theta2下的损失函数值
result1_ = np.array([loss_function(x, y, i, theta2) for i in theta1_space])
result2_ = np.array([loss_function(x, y, theta1, i) for i in theta2_space])# 创建一个新的图形对象
fig1 = plt.figure(figsize=(8, 6))
# 添加第一个子图，展示theta1变化时的损失函数值
plt.subplot(2, 2, 1)
plt.plot(theta1_space, result1_)# 添加第二个子图，展示theta2变化时的损失函数值
plt.subplot(2, 2, 2)
plt.plot(theta2_space, result2_)# 添加第三个子图，使用等高线图展示theta1和theta2的损失函数值
plt.subplot(2, 2, 3)
theta1_grid, theta2_grid = np.meshgrid(theta1_space, theta2_space)
loss_grid = loss_function(x, y, theta1_grid, theta2_grid)
plt.contour(theta1_grid, theta2_grid, loss_grid)# 添加第四个子图，使用更多等高线展示损失函数值的分布
plt.subplot(2, 2, 4)
plt.contour(theta1_grid, theta2_grid, loss_grid, 30)# 创建第二个图形对象，用于展示损失函数值的三维表面图
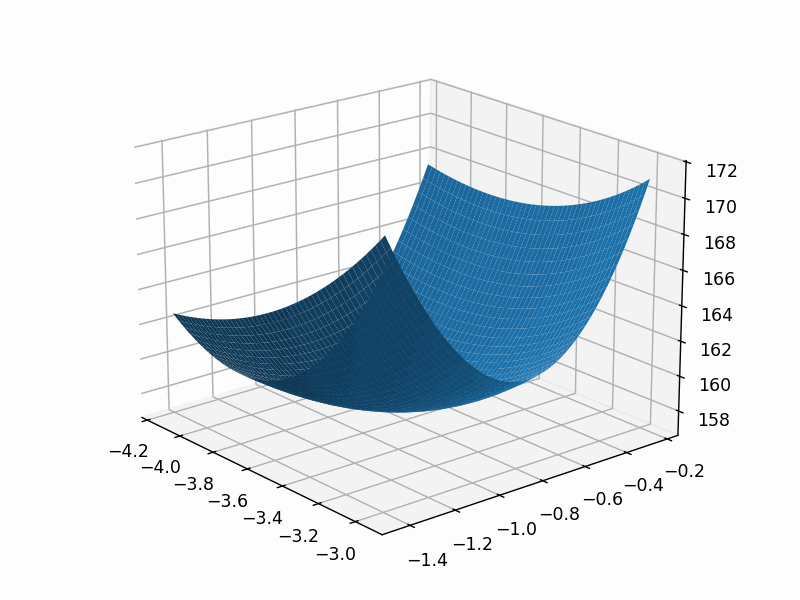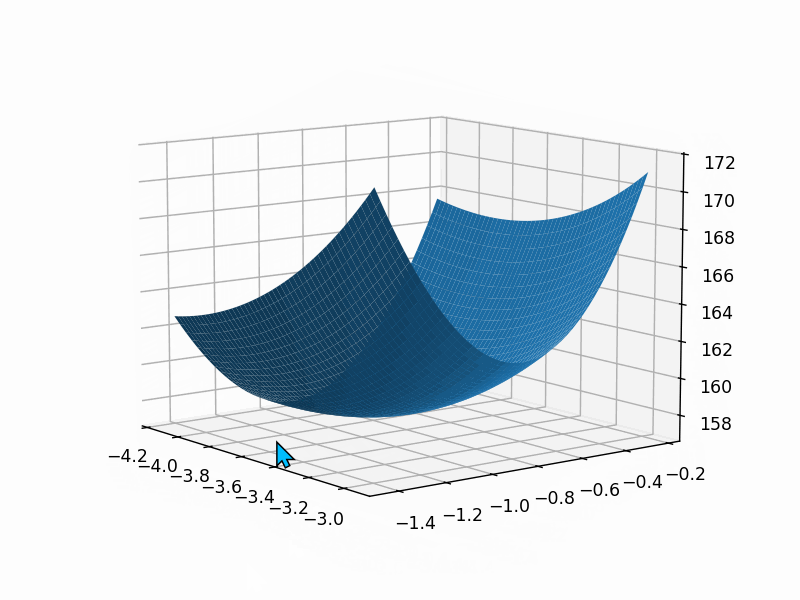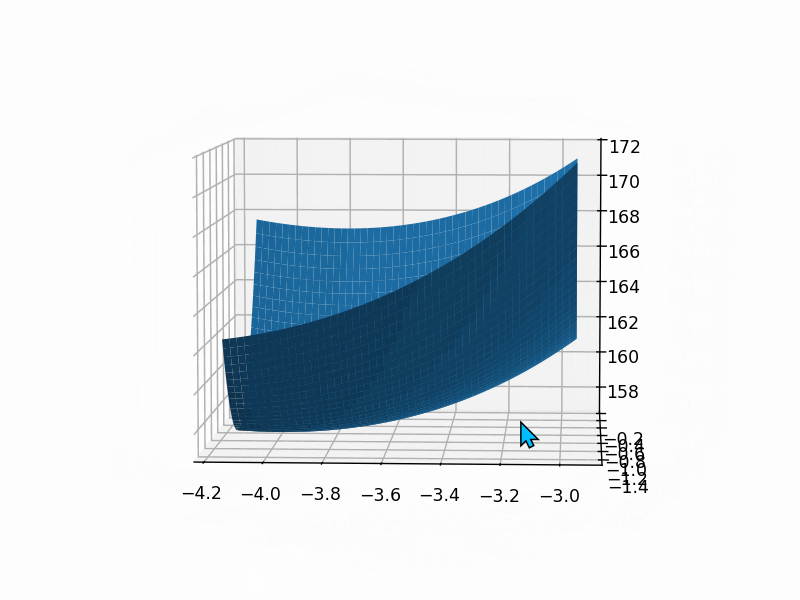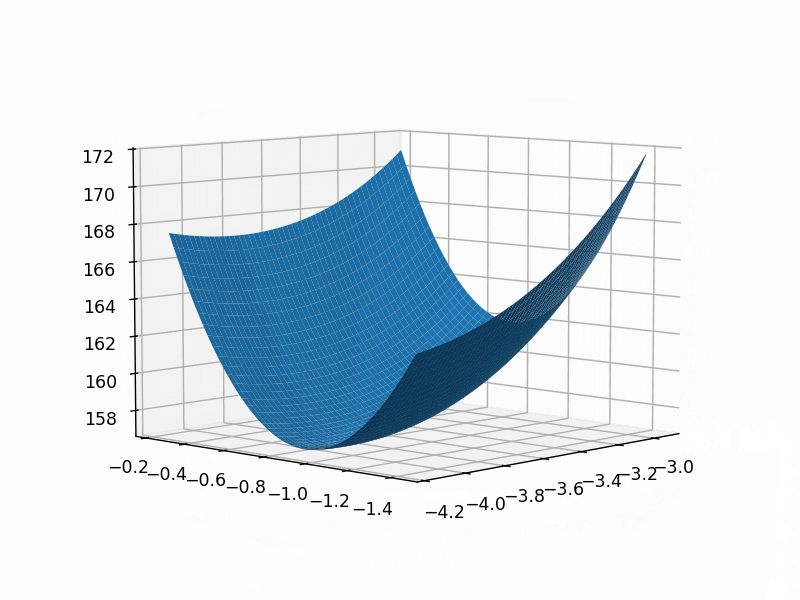
fig2 = plt.figure()
# ax = Axes3D(fig2)
ax=fig2.add_axes(Axes3D(fig2))
ax.plot_surface(theta1_grid, theta2_grid, loss_grid)plt.show()