当前位置：首页 > news >正文

DES密码系统的差分分析

news 来源：原创 2025/4/28 10:51:27

一、基本介绍

80年代末，Eli Biham与Adi Shamir提出的一种选择明文攻击方法，最初是针对DES，后来的分析表明他们对几乎所有的分组密码都适用。

设计者提出一个新的分组密码算法时，都要考虑该密码抵抗差分分析的能力。

很多基于差分分析的攻击方法：不可能差分，截断差分，高阶差分，飞去来器（Boomerang）攻击，矩形（Rectangle）攻击，仍然是现代密码算法最有效的攻击手段。

差分分析是什么？

差分分析方法是密码学近30年发展中最具意义的成果之一。不仅能用来攻击分组密码算法，对Hash函数同样适用。它是迄今已知的攻击迭代密码最有效的方法之一，其基本思想是：通过分析明文对的差分值对密文对的差分值的影响来恢复某些比特秘钥。本质上是研究差分在加解密中的概率传播特性。

差分密码分析属于选择明文攻击方法,它通过研究特定的明文差分值在加密过程中的概率传播特性,将分组密码与随机置换区分开,并在此基础上进行密钥恢复攻击。

差分值是什么？

这里的差分值主要是指异或差分。

设X和X’是密码算法F的两个输入明文，则ΔX = X⊕ X’是他们的输入差分。令Y=F（X）和Y’=F（X’）是密码算法的输出，则ΔY=Y⊕ Y’是他们的输出差分。

给一个论文：Biham, E., Shamir, A. Differential cryptanalysis of DES-like cryptosystems. J. Cryptology 4, 3–72 (1991).

二、DES算法-Feistel 结构

他基本的feistel结构其实可以看成：（这里简化成八轮）

（这里攻击者可以剥离IP置换和逆置换）

关于des相关算法的基本内容，我推荐大家去小破站看视频哈，有一些大佬讲得非常好，不开玩笑，有些视频我自己已经看过很多遍了。这里简单介绍des中间的16轮迭代：分为E扩展、轮密钥加、S盒代换和P置换四个模块。

E扩展将32bit扩展成48bit长度的串，将初始分成长度为4的字符串，前加上上一个的尾，位加上下一个的首完成扩展。

轮密钥加每轮将E(Ri-1)⊕Ki，得到结果，每轮的k会有固定的算法变换，这里不做详细讲解。

S盒就是查表，长度为6的bit串，首尾两位确定行的二进制表示，中间四位确定列的二进制表示。将48bit缩短成32bit。会使用8个S盒，每个S盒都是一个4*16的矩阵便于我们查表从而替代。

P置换大抵也可以理解成查表。

Biham和 Shamir在1990年国际密码年会上第一次提出了对DES 算法的差分攻击,从此掀起了密码分析的热潮。

鉴于此,密码学杂志Journal of Cryptology在1991年以专刊方式详细刊登了Biham和 Shamir 的这项创新工作.Springer 出版社也在1993年出版了Biham和Shamir的专著,介绍 DES类密码的差分分析方法及其应用。

des的迭代流程

谁是非线性的？

DES的轮函数F包含E扩展，P置换，S盒，子秘钥异或，异或几种操作。这其中除了S盒以外的部件都是线性部件。

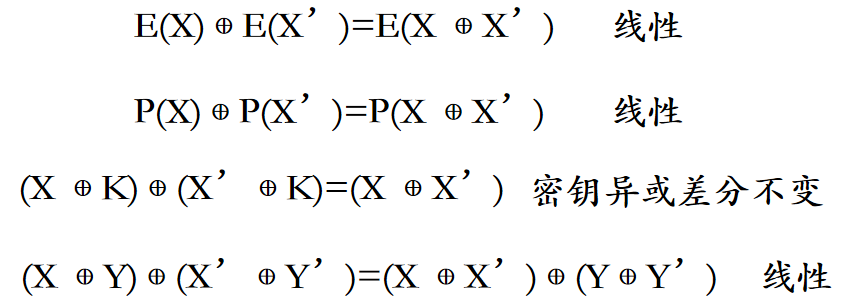
S盒是非线性的，输入对的异或差分不能确定输出对的异或差分。通常是输出差分有几个可能的值。

一个好的S盒应该保证对于一个确定的输入差分值，输出差分是均匀分布的。但是对于DES来讲，并不是所有的输出差分都会出现，而且分布也不是均匀的。

DES的设计在历史上有着争议，存在暗箱操作的可能性，而且在设计DES的时候学术界推测已经有差分分析存在。16轮的设计猜测是基于差分分析。

在分析之前的一些规定

nx ：十六进制数用下标 x 表示（即 10x=16）。一定要记住是16进制，后续很多换算以四字节为单位（16进制）而不是单个字节（二进制）。

X*、X'：在对消息对进行加密的任何中间点，X 和 X∗ 分别是该算法两次执行的相应中间值，并且 X′ 定义为 X′=X⊕X∗ 。

P(X) ：P 排列用 P(X) 表示。请注意，作为变量的 P 表示纯文本。

E(X) ：E 扩展用 E(X) 表示。

P：经过已知初始置换IP后的明文记为P。P∗是该对中的另一个明文，且P′=P⊕P∗是明文的异或结果。

T：相应明文 P 和P∗（在逆初始置换IP−1之前）的密文分别用 T 和T∗表示。T′=T⊕T∗ 是密文的异或。

(L,R) ：明文 P 的左半部分和右半部分分别用 L 和 R 表示。

(l,r) ：密文 T 的左半部分和右半部分分别用 I 和 r 表示。

a,...,j ：F 函数在各个回合中的 32 位输入。注意 a=R 。

A,...,J ：不同轮次中 F 函数的 32 位输出。Si ：S 盒 S1、S2 ..... S8。

SiEX ， SiKX ， SiIX ， Siox ：在第 X 轮中 Si 的输入用 SiIX 表示为 X∈ a,...,j。第 X 轮中 Si 的输出用 Siox 表示。进入 S 框 Si 的 6 个子键位的值用 SiKX 表示，扩展数据 (E(X)) 的 6 个输入位的值用 SiKX 进行异或运算形成

三、实际分析

我们从三轮des开始分析

S盒的差分性质：

首先我们明确一个概念叫做S盒的差分分布表：显示S盒的所有输入差分和输出差分分布的表格被称为S盒的差分分布表。

一个假设

举一个例子，假设4-bit的S如下定义：

遍历输入m的所有可能，并计算相应的m^′=m⨁f。

由上图可得：输入差分是f，输出差分是d，6,4，f。 不随机现象！ 如果是随机的，应该是均匀分布。

详细解释一下，输入差分是f，将该差分支拆解成可能的输入值为i、j所列举的。这是我们的输入，我们将输入的通过上面那个窄的s盒表格得到对应输入的输出。将这些对应的输出值进行差分异或运算。得到的值为上表的最后一列。通过穷举，我们能知道输入差分f的时候，输出差分只能是d64f。

（大家可以去试一下输入差分为1时，输出差分为？）

看真的

现在不假设，我们来看真的S盒，给定DES的第一个S盒如下：

遍历输入的所有可能输入差分，并计算相应的输出差分。输入6位，输出4位。

在这个表格中，每一行对应一个特定的输入差分，每一列对应一个特定的输出差分，表格中的数字代表具有这样输入差分和输出差分的可能对数。（就像刚刚假设当中输出差分f有两对，不信？自己翻回去数）

差分分布表的每行包含64个可能的配对，在16个不同的条目中。因此，在表中的每行，条目的平均值正好是4。（可以拿几个算一下，比如输入差分为0，这很好算了，避免特例我还是选择了34x的输入差分算了一下）

表格的第一行显示，对于零输入差分，输出差分也必须是零。此外，表中的不同行有不同的输出差分分布。

设X为一个六位值，Y为一个四位值。当存在某个输入异或值等于X且输出异或值等于Y的S盒配对时，我们称X可能通过该S盒导致Y。若存在此类配对则记为X→Y，若不存在则称X不可能通过该S盒导致Y并记为X（不导致）（就是箭头画一撇啦，不知道咋打出来）Y。

考虑输入异或值S1i '= 34x的情况。它仅有八种可能的输出异或值，而其他八种组合则不可能出现。可能的输出异或值S1O ’包括1x、2x、3x、4x、7x、8x、Dx和Fx。因此，输入异或值34x可能导致输出异或值1x（记作34x → 1x）。同理也存在34x → 2x和34x → Fx的对应关系。但34x →（不导致） 0x和34x →（不导致） 9x这两种情况则不会发生。

我们加入概率来看

对于一个固定的输入差分，可能的输出差分并不具有均匀分布。以下定义扩展了上述定义，加入了概率。

定义：我们称当S盒的输入异或值为X时，若其中输出异或值为Y的配对占比为p，则X可能以概率p引发Y。

示例：34x→2x放大结果来自S1的64对组合中的16对，即概率为1/4。34x→4x结果仅来自S1的64对组合中的2对，即概率为1/32。

表格的不同行中呈现出不同分布。总体而言，70%至80%的条目是可能的，20%至30%的条目是不可能的。每个S盒的具体百分比如下表所示。

我们估算可能条目占比约为80%。通过异或分布表对，可以根据给定的输入输出异或值找出配对可能的输入输出值。

示例：考虑S1异或分布表中34x→4x这个条目。由于该条目值为2，意味着仅有两组配对满足这些异或条件。这两组配对互为对偶——若第一组是S1I与S1*I，则另一组必为S1*I与S1I。通过查看表5（下表）可知，这两组输入必定是13x和27x，其对应输出分别为6x和2x。

或许你想问2x和6x咋来？看这个

一个例子

示例：考虑S1并假设输入对为S1E=1x、S1E*=35x，且对应六个关键位的值为S1K=23x。

计算实际输入和输出

那么S1的实际输入（在输入位与关键位进行异或运算后）为S1I=22x、S1I*=16x，输出分别为S1O=1x、S1O*=Cx。输出异或结果为SlO'=Dx。

我们详细来看，根据规则实际输入是将输入与密钥位进行异或，即：

S1I=S1E⊕S1K=1x⊕23x=22x， S1I∗=S1E∗⊕S1K=35x⊕23x=16x。

（S1I中的I是input的简写，为输入）

（举个例子：16x咋来？再解释一遍）

输出计算：通过查询 S1 盒的映射关系，得到输出分别为S1o=1x，S1o∗=Cx。（o为output的简写，为输出）

（你又要问输出咋来的？，再看）

寻找密钥值（往回推）

假设已知S1E = 1x、S1E*= 35x且SlO'=Dx，现需求解密钥值S1K。

无论S1K的实际值为何，输入异或值S1E'= S1I'=34x恒定（S1E′=S1I′=S1E⊕S1E∗=1x⊕35x=34x、输入异或值与S1K无关）。通过查证表5可知，S盒的输入存在八种可能情况。如表6所述，这八种输入可能性对应着八种密钥可能性。表中每行数据描述了两组具有相同输入但顺序相反的数据对。每组数据对可推导出一个密钥值，因此每行数据对应两个密钥值。正确的密钥值S1K必然存在于该表中。

为了进一步确定正确的密钥，使用额外的输入对，如S1E=21x，S1E∗=15x（选这一对是因为两个异或也为34x）（S1K仍假设为23x ）。重复上述计算过程，得到新的输出异或S1o'=3x ，以及对应的可能输入和密钥（如 Table 7 所示）。

可以理解成，通过使用额外的输入对，我们可以为S1K获得更多候选值。以输入对S1E=21x、S1E*=15x（保持相同S1K=23x）为例，S盒的输入为S1I=2x、S1I*=36x，输出为S1O=4x、S1O*=7x，此时输出异或值为S1O'=3x。表7列出了所有满足34x→3x的S盒可能输入值及其对应密钥。

正确的密钥必须同时出现在两个表格中，而表6与表7中仅有的共同密钥值为17x和23x——由于当前输入异或值的限制，这两个密钥值无法被区分。由于17x⊕23x=34x=S1E′，在当前输入异或值下这两个值无法区分，但使用不同输入异或值的对就可能将它们区分开，从而确定唯一的正确密钥。

（解释一下为什么17x⊕23x=34x=S1E′）

扩展到三轮des系统中

已知P=(PL,PR)和P*；C=(CL,CR)和C*。

要求：PR的33,34,35,36 比特差分是0

示例：假设我们有一个密文对，其明文异或值已知，且明文异或的第64、33、......、37位六个比特均为零（A的第一个S盒的输入）。第一轮输入异或中进入S1盒的所有比特均为零（S1Ea'= S1Ia' = 0），因此第一轮S1盒的输出异或必然为零（S1Oa' = 0）（A的第一个s盒对应的值）。

由图：密文的左半部分是通过将明文的左半部分、第一轮输出和第三轮输出进行异或运算得出的。（为啥？看图）CL=PL ⊕A ⊕C

由于已知明文异或(PL)与密文异或(CL)，且首轮S1盒的输出异或(A)亦为已知量，因此可计算出第三轮S1盒的输出异或(C)。第三轮的输入对（S1Ec, S1Ec*）能轻易从密文对中提取获得。

若第三轮中S1的输入对为S1Ec = 1x，Sl*Ec = 35x且输出异或值为S1Oc' = Dx，则可按示例7所示方法求出S1Kc的值，该值必出现于表6中。通过使用额外输入对，我们可以逐步排除部分可能值，直至获得S1Kc的唯一解。由于S1Ec'非常量，故该子密钥应不存在不可区分的情况。

一个题目（分析DES第三轮密钥的前六个bit）

这里为什么是前6个bit，因为S盒是每六个bit为一个，这样的话我们可以不用分析很多的S盒，前六个bit也就直接对应S1盒的输入密钥。

题目说，选择明文PR的64,33，……37比特差分为0，即P和P*的64,33……37比特相同，得到相应密文C，C*。

输入输出差分，根据差分分布表中的值，求异或得Ki。

密文CR由C已知，CR*由C*已知，即C'=C异或C*已知，输入差分确定。由这个公式CL=PL ⊕A ⊕C，（因为相互异或，此时C = PL ⊕A ⊕CL）输出差分为C'=C异或C*。所以推算的逻辑链条变成：A→C→K3。

通过这个图：

选PR的64,33，……37比特差分为0，（P,C),(P*,C*)输入差分为0，所以输出差分为0。则A = P（0*** ****),C = PL ⊕CL⊕A = PL ⊕CL⊕P(0*** ****)(这里加P是S盒之后要经过P置换）

（C) = (CL)⊕(PL) ⊕(0*** ****)(P逆置换把A前面的P消掉）

求出S1盒后的输出差分。

因为输入差分E（C)可知，根据查差分分析表得可能的输入，将这些值和E(C)异或，得到可能的密钥集。选取不同明密文对，重复差分分析操作，得到结果相交。得到确定的密钥集，即前六个bit。

（当时看这个很懵，现在我浅显的理解成，第三轮CL,CR已知，其实输入差分已知，我们要求输出差分，而因为公式，输出差分等于CL异或PL异或A，只有A不知道，我们要求A。输出差分要求固定，这个时候只有当A第一轮的输入输出都等于0时，才可能不变，所以我们将他们换成0。最后又一轮P的逆置换，得到输出差分，而因为前面那个小的EK得O的流程表，EO都已知，K只需要不断试验求交集即可。（像一个例子中的第二问））

n轮特征

定义：与任何一对加密相关联的是其两个明文的异或值、其密文的异或值、两次执行中每轮输入的异或值，以及两次执行中每轮输出的异或值。这些异或值构成一个n轮特征。特征具有概率性，即一个具有选定明文异或值的随机对，其轮次与密文异或值符合该特征的概率。我们用 ΩP 表示特征的明文异或，用 ΩT 表示其密文异或。

以下示例描述了一个概率为1的单轮特征。这是唯一一个概率大于1/4的单轮特征。该特征非常实用，可应用于任何类DES密码系统。

对于任意的L′ ，该特征可表示为ΩP=(L′,0)，意味着两个参与加密的明文，其右半部分的异或值为 0。在加密过程中，a′=0→A′=0始终成立，即 F 函数输入异或为 0 时，输出异或也为 0，概率为 1。经过 F 函数运算后，得到ΩT=(L,0)，表示密文的右半部分异或值也为0 。

在这种单轮特征中，除一个S盒外，所有S盒的输入异或值均为零（概率为1的图）。被选中的非零输入异或值S盒，其选择标准是最大化该输入异或导致特定输出异或的概率。由于经E扩展后存在多个输入比特会同时进入两个相邻S盒，我们必须确保这些比特的异或值为零。每个S盒仅有两个私有比特位，这些比特可以具有非零异或值。对于S1盒而言，最佳概率为14/64（即存在一个包含14对输入输出的条目，该条目不会导致相邻S2或S8盒的输入变为非零）。因此，很容易构建出概率为14/64的单轮特征。

具体表现为：S1盒：十六进制0C→E，概率14/64；

S2至S8盒：十六进制00→0，该转换始终成立。

以下示例描述了一个概率为14/64的简单单轮特征。

（ΩP表示明文对的差异（在差分密码分析语境下）。这里它由两部分组成，L′ 可以理解为明文对左半部分的差异（具体内容未明确给出），60000000x 是十六进制表示的右半部分差异值。这是进入加密流程前设定的明文对差异情况，是整个分析的起始点。

A′=00808200x ：这是 F 函数的一个输入值，在 DES 加密的 F 函数运算中，它是经过一些前期处理（如扩展置换等）得到的中间数据。这里00808200x 是十六进制形式。同时，A′=P(E0000000x) ，这里P可能代表某种置换操作，E可能是扩展操作，即A′是对E0000000x 经过P操作得到的结果。

a′=60000000x ：这是 F 函数的输出结果，是经过 F 函数内部一系列运算（如 S 盒替换、P 盒置换等）后得到的十六进制表示的数据。并且图中注明了这一输出结果出现的概率是6414 ，这意味着在特定的输入条件下（即前面提到的明文对差异等情况），F 函数输出为a′=60000000x 这种情况在所有可能情况中占比为6414 ，这个概率值是通过对 S 盒的 XOR 分布等特性分析得到的。

ΩT=(L′⊕00808200x,60000000x) ：ΩT表示密文对的差异。它的左半部分是L′（明文对左半部分差异）与00808200x（F 函数的一个输入值）进行异或运算的结果；右半部分就是 F 函数输出的a′=60000000x 。这就是经过一轮加密后，根据输入的明文对差异和 F 函数运算得到的密文对差异情况。）

在 S2或者S6 中使用非零输入异或可以产生概率为 1/4 的一轮特性。

以下示例描述了一个通过将上述两个概率图中所述的两个单轮特征串联起来而容易获得的双轮特征：

现在我们来给出n轮特征的定义。

定义 7.n 轮特征是一个元组 Ω=(ΩP,ΩΛ,ΩT)，其中 ΩP 和 ΩT 是 m 位数字，ΩΛ 是 n 个元素的列表，每个元素 ΩΛ=(Λ1,Λ2,...,Λn) .其中一对形式为 Λi=(λIi,λOi)，其中 λIi 和 λOi 是 (m/2) 位数，m 是加密系统的块大小。

特征满足以下条件： λI1 = ΩP 的右半部分， λI2 = ΩP 的左半部分⊕λo1 ， λIn = ΩT 的右半部分， λIn−1 = ΩT的左半部分⊕λOn 。

并且，对于每个 i，使得 2≤i≤n−1，。

对于一个 n 轮特征Ω=(ΩP,ΩΛ,ΩT)和一个独立密钥 K，一个正确对是指满足P′=ΩP，并且在使用独立密钥 K 对该对进行加密的前 n 轮中，第 i 轮的输入异或等于λIi，F 函数的输出异或等于λoi的一对。每一个相对于该特征和独立密钥而言不是正确对的对，都称为相对于该特征和独立密钥的错误对。

n轮特征 Ω1=(ΩP1,ΩΛ1,ΩT1) 与 m轮特征 Ω2=(ΩP2,ΩΛ2,ΩT2) 的连接，其中 ΩT1 等于 ΩP2 两半的交换值，为特征 Ω=(ΩP1,ΩΛ,ΩT2) ，其中 ΩΛ 是列表 ΩΛ1 和 ΩΛ2 的连接。

好，现在我们开始上公式了。（主播已经感觉快把自己差分了看不懂啊）（受不了了感觉这些公式好难打我要自己写...）

（我理解成分布和整体的连乘关系）

所以！每个 n 轮特征都可以描述为 n 个一轮特征与概率的串联，概率是一轮特征概率的乘积。

定义：特征Ω=(ΩP,ΩΛ,ΩT)的形式化定义概率，是指在使用随机独立密钥时，任何满足P′=ΩP的固定明文对为正确对的实际概率。

将上述一轮和二轮串联，可实现三轮特征的扩展。由此得到一个三轮特征，其概率为(14/64)²=0.05，该特征在第四轮满足d'=b'⊕C'=C'=A'的条件。

我们发现，当明文在五个特定位位置存在差异时，约有0.05的概率会导致第四轮输入处仅出现三位差异。经过位扩展后，五个S盒具有非零输入异或值，三个S盒具有零输入异或值（因而输出异或值也为零）。在此情况下，可通过公式e' = c' ⊕ D'推导出e'的12位信息。

这种中间轮次采用零输入异或的三轮结构极具实用价值，为三轮特征构建了最优概率条件。

类似结构可应用于五轮特征中。中间轮次的输入输出异或值为零，且存在对称性——即在第六轮中f' = d'⊕E' = b'⊕A' = L’。字符串b'→a'→A'的存在确保了此类五轮特征的成立。该特征概率极低，因为在b'→a'和a'→A'两轮中需有三个S盒输入同时产生差异，整个五轮特征中共需六个差异点。单个S盒的最佳差分概率为16/64=1/4，这使得五轮特征的总概率上限不超过(1/4)⁶=1/4096。实际上目前已知最佳五轮特征的概率约为1/10486。