Python----卷积神经网络(卷积为什么能识别图像)
一、卷积的概念
卷积是一种数学运算,通常用于信号处理和图像分析。在卷积神经网络中,卷积操作用于提取输入数据(如图像)中的特征。通过将输入数据与卷积核(滤波器)进行卷积运算,CNN能够识别图像中的边缘、纹理和其他重要特征。
二、卷积核的概念
卷积核(或称为滤波器)是一个小矩阵,通常比输入数据的尺寸小。卷积核在输入图像上滑动(即进行卷积运算),计算在其覆盖区域内的加权和,从而生成特征图(feature map)。卷积核的参数通常是可以学习的,训练过程中会自动调整以优化模型的性能。
卷积核其实是一个小矩阵,在定义时需要考虑以下几方面的内容:
卷积核的个数:卷积核的个数决定了其输出特征矩阵的通道数。
卷积核的值:卷积核的值是自定义的,根据想要提取的特征来进行设置的,后续 进行更新,就像全连接中的 一样,只是乘积运算变成卷积运算。
卷积核的大小:常见的卷积核有1x1、3x3、5x5等,注意一般都是奇数x奇数。
三、卷积的过程
卷积过程包括以下几个步骤:
-
选择卷积核:定义一个大小为 K×K 的卷积核。
-
滑动卷积核:将卷积核从输入图像的左上角开始,向右和向下滑动,逐步覆盖整个图像。
-
计算加权和:在卷积核覆盖的区域,按元素相乘并求和,生成输出特征图的相应位置的值。
-
重复:继续移动卷积核,直到覆盖完所有位置。
卷积的过程是将卷积核在图像上进行滑动计算,每次滑动到一个新的位置时,卷积核 和图像进行点对点的计算, 并将其求和得到一个新的值,然后将这个新的值加入到特征图中,最终得到一个新的 特征图。

第一次卷积就是从输入特征矩阵的左上角开始,通过点对点的计算,就是1x0、 0x0、0x1、0x0等计算,并将其乘积的结果加起来,得到一个新的值1,这就完成第 一次卷积操作。
接着卷积核就会在输入特征矩阵上不断的滑动卷积,先向右,到最右边之后,就会向 下移动一格,然后从最左边开始向右滑动。也就是说,卷积过程秉持着先左后右、先 上后下的移动规律进行卷积,直到右下角位置为止。
可以通过不断调整卷积核的大小、卷积核的值和卷积操作的步长,可以提取出不同尺 度和位置的特征。
可以看到,用一条右上到左下的卷积核去和输入特征做卷积,得到的结果 中,从右上到左下的值变的比其它地方的大。
根据分类算法中Softmax和交叉熵的理解,当一个地方的值变大之后,这个值会使得 整个概率分布更加偏向于这个地方, 也就是说,这个地方的概率会变得更高。
因此,从Softmax和交叉熵的角度来看,这 个位置的值变大是一个好的预测结果。 在交叉熵损失函数中,它衡量了模型输出的概率分布与实际标签的分布之间的差异。
具体来说,当某一类别的概率较大而实际标签对应的类别为1时,交叉熵损失较小; 反之,如果概率较小而实际标签对应的类别为1时,交叉熵损失较大。
因此,通过提高某一特定特征区域的值,模型更加关注这一特征,有助于提高对应类 别的概率得分,从而改善模型的性能。
四、步长
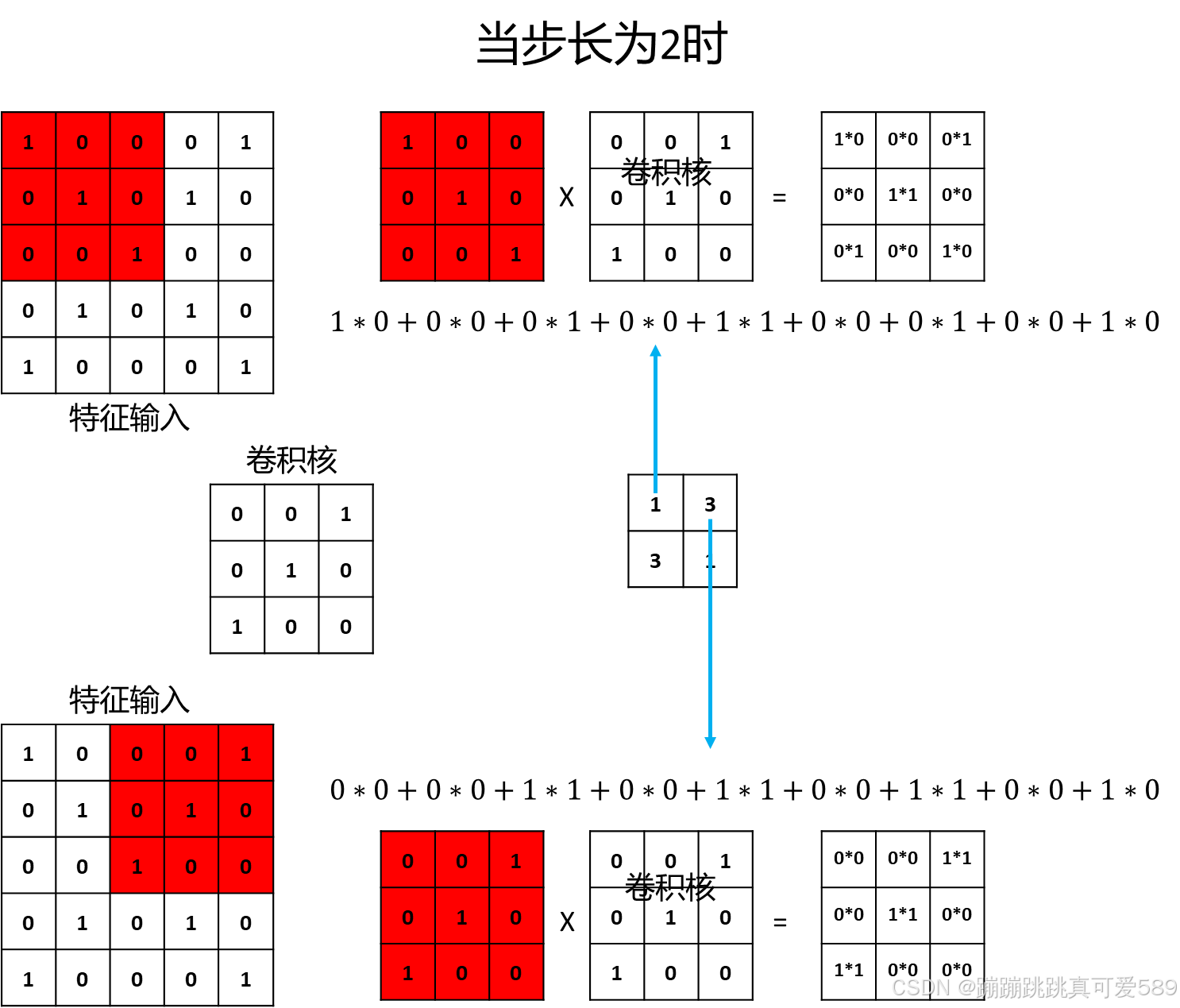
步长(stride)是指卷积核在输入数据上滑动的步幅。步长的大小影响输出特征图的尺寸。步长为1时,卷积核每次移动一个像素;步长为2时,卷积核每次移动两个像素。步长的选择对卷积层的计算量和特征图大小有直接影响。
五、Padding
Padding(填充值)是指在输入数据的边缘添加额外的像素,以控制输出特征图的大小。Padding 可以帮助在卷积过程保持空间信息,尤其是当卷积核在输入边缘时。通常使用填充(Padding)操作来增加图像的大小,以便在应用卷积操作时保持输出 特征图的大小与输入特征图相同或更接近。常用的 Padding 类型包括“VALID”和“SAME”。
5.1、VALID
VALID Padding(有效填充)意味着在进行卷积运算时,不在输入图像的边缘添加任何填充值。结果是输出特征图的尺寸会小于输入图像的尺寸,因为卷积核无法覆盖到所有输入数据的边缘。

5.2、SAME
SAME Padding(相同填充)意味着在进行卷积运算时,向输入图像的边缘添加填充值,以确保输出特征图的尺寸与输入图像相同(在步长为1的情况下)。这样可以保持特征图的空间结构,同时又允许卷积核充分利用输入数据。

六、 卷积核为什么总是选择奇数大小
在深度学习中,卷积核的大小一般选择奇数是为了方便处理和避免引入不必要的对称性。
当卷积核的大小是奇数时,它具有唯一的一个中心像素,这个中心像素点可以作为滑 动的默认参考点,即锚点。 这使得在进行卷积操作时,卷积核可以在输入图像的每个像素周围均匀地取样。这样 的好处是,在进行卷积操作时,可以保持对称地处理图像的每个位置,从而避免引入 额外的偏差和不对称性。
相反,如果卷积核的大小是偶数,那么在某些位置上,中心 像素会落在两个相邻的像素之间,这可能导致对称性问题。
此外,选择奇数大小的卷积核还有一个重要的优点是,在进行空间卷积时,可以确保 卷积核有一个明确的中心像素,这有助于处理图像的边缘和边界像素,避免模糊和信 息损失。 当然,并不是所有情况下都必须选择奇数大小的卷积核。
在某些特定情况下,偶数大 小的卷积核也可以使用,并且在某些特定任务中可能表现得更好。但是在大多数情况 下,奇数大小的卷积核是一种常见且推荐的选择,因为它可以简化卷积操作,并有助 于保持图像处理的对称性和一致性。
七、设计思路
import tensorflow as tf # 输入特征张量
# [batch_size, input_height, input_width, in_channels]
# 这里创建了一个形状为 (1, 5, 5, 1) 的输入张量,代表一个批次,大小为5x5的图像,1个通道
input = tf.constant([[ [[1], [0], [0], [0], [1]], [[0], [1], [0], [1], [0]], [[0], [0], [1], [0], [0]], [[0], [1], [0], [1], [0]], [[1], [0], [0], [0], [1]]
]], dtype=tf.float32) # 卷积核张量
# [kernel_height, kernel_width, in_channels, out_channels]
# 这里创建了一个形状为 (3, 3, 1, 1) 的卷积核,代表3x3的滤波器,1个输入通道,1个输出通道
wc1 = tf.constant([[ [[0]], [[0]], [[1]]], [[[0]], [[1]], [[0]]], [[[1]], [[0]], [[0]]]
], dtype=tf.float32) # 创建卷积层
# 使用 tf.nn.conv2d 进行卷积操作,strides=[1, 1, 1, 1] 表示在每个维度上移动1步,padding='SAME' 填充使输出与输入相同大小
conv_layer1 = tf.nn.conv2d(input, wc1, strides=[1, 1, 1, 1], padding='SAME') # 将卷积的输出转为 NumPy 数组
output1 = conv_layer1.numpy() # 获取卷积层输出特征图的形状
batch_size = output1.shape[0] # 批次大小
height = output1.shape[1] # 高度
width = output1.shape[2] # 宽度
channels = output1.shape[3] # 通道数 # 打印卷积后特征图的形状和值
print(f"卷积后的特征大小: [batch_size={batch_size}, height={height}, width={width}, channels={channels}]")
print("输出特征图:", output1.reshape(height, width)) # 以 (height, width) 的形状打印输出特征图 