空洞/膨胀卷积

1.简介

膨胀卷积又叫空洞卷积，最初的提出是为了解决图像分割的问题，常见的图像分割算法通常使用池化层和卷积层来增加感受野(Receptive Filed)，同时也缩小了特征图尺寸，然后再利用上采样来还原图像尺寸，特征图缩小再放大的过程造成了精度上的损失，因此需要一种操作可以再增加感受野的同时保持特征图的尺寸不变，从而代替下采样和上采样操作。

2.作用

• 增大感受野

• 保持原输入特征图W、H

• 在实际使用中，一般都会对padding进行设置（将padding设置为1），这样就能保证输入特征图的高度和宽度不变。

2.1 为什么要使用膨胀卷积

在语义分割中，通常会使用分类网络作为backbone。通过backbone之后会对特征图进行一系列的下采样，之后再进行一系列的上采样还原原图的大小。

在分类网络中，一般都会对图片的高度和宽度下采样 32 倍。由于后续需要通过上采样还原到原来的尺寸，所以如果下采样的倍率很大时，使用上采样还原回原来的尺寸，这个过程就是导致比较严重的信息丢失。

以 VGG16 为例，该网络通过 MaxPooling 层对特征图进行下采样：

通过 MaxPooling 会降低特征图的 shape
MaxPooling 会丢失特征图的一些细节信息（毕竟是用最大值代替局部值，丢失信息是肯定的）
丢失的信息和目标是无法通过上采样进行还原的
这就导致在语义分割任务的效果不理想。

• 1.空洞卷积可以在不改变输出图像的特征图的尺寸的情况下增大感受野(前提是需要进行合适的padding)
• 2.空洞卷积能够在不增加参数的前提下增加感受野的大小
• 3.通过连续的卷积，膨胀卷积的感受野呈指数增加

2.2简单堆叠膨胀卷积的问题

在膨胀卷积使用的过程中经常会遇到一个名叫 gridding effect 的问题。

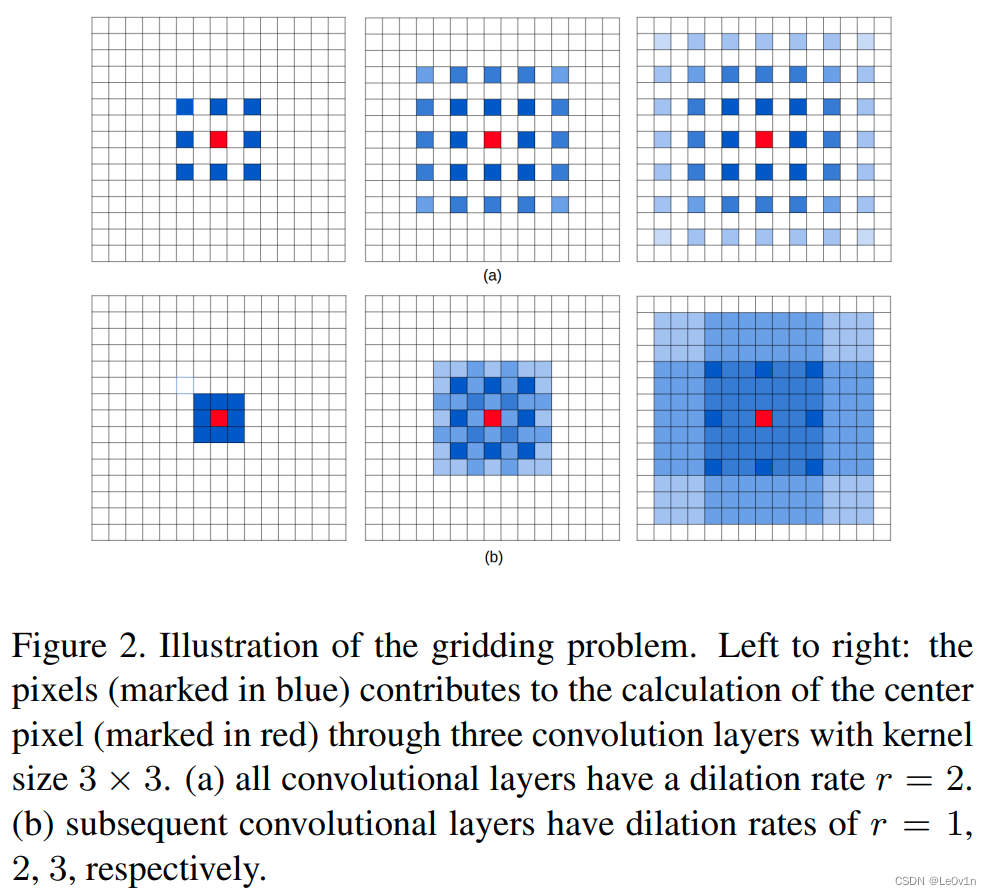
什么是gridding effect —— 连续使用几个膨胀系数相同的膨胀卷积

连续使用3个膨胀卷积层（卷积核大小都为3×3，膨胀系数均为2）

因为没有利用到所有的像素值，所以一定会丢失一部分细节信息 —— 和MaxPooling一样（但是比MaxPooling要轻微）

所以在使用膨胀卷积时要尽可能避免 gridding effect 问题（不要连续使用多个膨胀系数相同的膨胀卷积）。

2.3 连续使用几个膨胀系数不同的膨胀卷积

2.4 两种方法对比

• 两种方法的参数数量是一样的
• 仅仅是膨胀系数不同而已

对于 r=[2, 2, 2] 这样连续相同的膨胀卷积来说，Layer4的感受野是13×13，但在这个视野下有很多像素值是没有利用到的。我们更加倾向于使用 r=[1, 2, 3] 这样不相同连续的膨胀系数 —— 感受野下使用的区域是连续的。

2.5 普通卷积与空洞卷积对比

• 直接使用普通卷积Layer4的感受野和前面的两种膨胀卷积不同
  • 膨胀卷积的感受野为 13×13
  • 普通卷积的感受野为 7×7
• 这说明使用膨胀卷积可以大幅度增加感受野

3. 膨胀卷积使用方法 —— Hybird Dilated Convolution (HDC，混合膨胀卷积)

3.1 论文中建议一：M2 ≤ K

使用 r=[1, 2, 3] 的膨胀系数和使用 r=[2, 2, 2] 膨胀系数的感受野是相同的，但前者对于输入信息的利用率高 —— 理论效果更好。

3.2 论文中建议二：将膨胀系数设置为锯齿形状

3.3 论文中的建议三：r  的公约数 ≤ 1

在连续使用膨胀卷积时，我们应该参考 HDC 的设计准则以保证高层可以有效利用低层的信息。