算法分享——弗洛伊德算法暴力破解多源最短路问题
算法简介:
弗洛伊德算法是一种求解“多源最短路”问题的算法
在弗洛伊德算法中,图一般用邻接矩阵存储,边权可正可负,但是(不能出现负环),整体思路是采用动态规划的思想求解任意两点间的最短距离。
准备工作:
我们只需要准备一个二维动态,规划数组dp[i][j]表示考虑到当前情况从点i到点j的最短距离,然后给数组初始化为无穷再不断更新最短距离。
算法复杂度分析:
由于需要循环来遍历中转点,起点和终点所以需要使用三层循环,时间复杂都是O(n3),复杂度很高,所以通常用来处理n<=500即图中的点的数量小于500的情况,这也是使用弗洛伊德算法的一个提示。
算法模板:

其中最外层循环表示遍历所有的中转点,次外层循环表示遍历所有的起点,最内层循环表示遍历所有的终点,其中状态转移方程:
![]()
表示加入中转点K后与不加入K时比较更新最短路径,这样任意两点的最短路径就会存储在dp数组中,我们根据需要取出即可。
实战应用:


这道题我们需要注意以下几点:
1.题目中给出了400个点是在提示我们可以使用弗洛伊德算法
2.需要注意自己到自己的距离始终为0,初始化要注意dp[i][i]=0
3.要注意无法到达应该输出-1
4.注意无向图的初始化要双向初始化
代码实现:

#include<iostream>
using namespace std;
using ll = long long;
const int N = 405;
const ll inf = 2e18;//定义无穷
ll dp[N][N];
int main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);//加速输入速度
int n, m, q;
cin >> n >> m >> q;
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
dp[i][j] = inf;//初始化无穷
}
dp[i][i] = 0;//自己到自己的距离始终为0,易错点
}
while (m--)//处理m条边权
{
ll u, v, w;
cin >> u >> v >> w;
dp[u][v] = min(dp[u][v], w);
dp[v][u] = min(dp[v][u], w);//无向图的初始化,w为两点间的边权
}
for (int k = 1; k <= n; ++k)
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
{
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
}
while (q--)
{
int st, ed; cin >> st >> ed;
cout << (dp[st][ed] >= inf ? -1 : dp[st][ed]) << "\n";//处理q次询问取出最短距离,路径不存在输出-1
}
return 0;
}
运行结果:

对输入输出的图解:
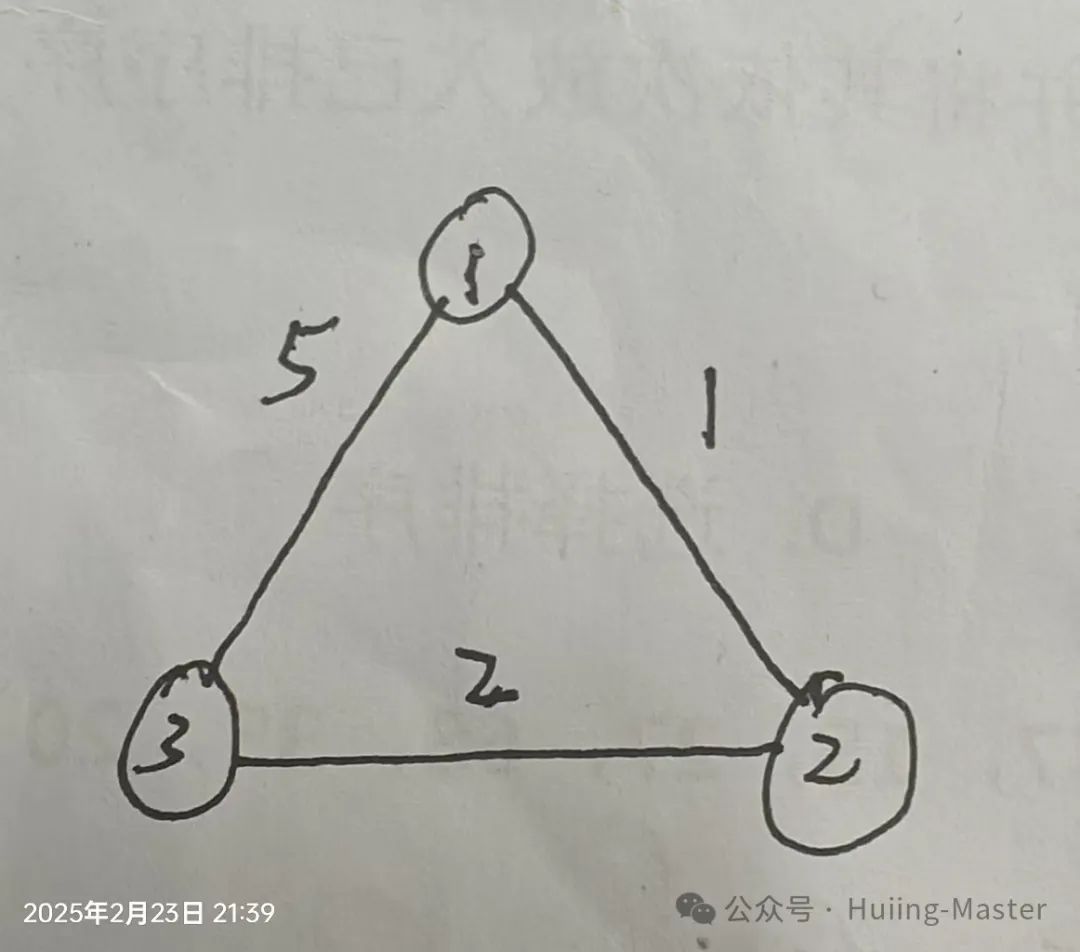
1到2的最短距离是1,1到3的最短距离是3,2到3的最短距离是2。
下一篇文章会介绍迪杰斯特拉解决最短路径问题。
