【自相关】全局 Moran’s I 指数
自相关(Autocorrelation),也称为序列相关性,指的是同一变量在不同时间或空间点的值之间的关系。简而言之,自相关就是一个变量与自身在不同位置或时间点的相关性
自相关:针对同一属性之间进行分析相关性
本质是:一个变量与它自己在不同位置或时间上的值之间的关系。
空间自相关则是针对空间数据,分析其“空间聚集性”或“分散性”
自相关分析:用相同大小的窗口,把数据切分成若干块,再计算数据间的相关性
把一整片数据(空间上的)分成小块,一块一块地看每块内部的数据是不是相关的,是不是存在某种聚集或分散的趋势。这种分析方式就叫做自相关分析,使用的是统一大小的窗口,目的是发现数据在空间上的分布规律
空间自相关
空间自相关描述的是空间单位之间的属性值是否具有一定的规律性或相似性。它帮助我们判断空间数据是否聚集、分散或随机分布
-
正空间自相关:如果相邻区域的属性值相似或相同(比如高房价的区域总是聚集在一起),则表现为正空间自相关。
-
负空间自相关:如果相邻区域的属性值相差很大(高房价旁边是低房价),则表现为负空间自相关。
-
无空间自相关:如果属性值在空间上没有明显的聚集或分散,属于随机分布。
随机——相邻区域同质与异质不确定;
聚集——相邻区域均同质;
离散——相邻区域均异质;
在空间上相邻的区域,它们的值是不是也“相邻”?——值是否有空间聚集性?
用通俗话讲:
高的值是不是和高值靠一起?
低的值是不是也扎堆?
还是高低混在一起没有规律?
这就叫“空间自相关”。
全局 Moran’s I 指数
衡量空间数据中相似值是否倾向于聚集在一起的程度
是一个 全局统计量(全局指标用于探测整个研究区域的空间模式,使用单一的值来反映该区域的自相关程:度),表示整个区域上的总体空间自相关性强弱

其他表示:
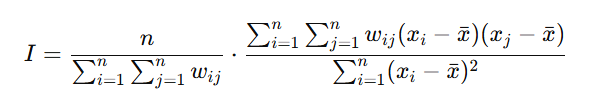

公式理解:
Moran's I 的思路:一个地区 i 的值,和它邻近地区 j 的值是不是类似。
分子:空间偏差乘积
第 i 个区域的值与平均值的差距(偏差)
两个区域(i 和 j)的偏差相乘
这个乘积的正负值代表了两者的相似程度
正值
两个区域的值都偏高或都偏低 → 相似
负值
一个偏高一个偏低 → 不相似
空间权重矩阵中的元素,表示区域 i 和区域 j 之间的空间关系
所有相邻区域之间的“趋势相似性”的加权和
分母:值本身的总离散程度
整个样本的方差(所有区域的偏差平方和),数据的离散程度
外层乘一个 调整因子:
让结果的数值范围大致落在 [-1, 1];
n:样本点数量
保证不同样本量、不同邻接结构下 Moran’s I 有可比性;
Moran’s I 结果解释
| I 值大小 | 空间解释 |
|---|---|
| I>0 | 正空间自相关(值相似的区域空间上靠近) |
| I=0(约等于) | 无空间自相关(值分布随机) |
| I<0 | 负空间自相关(值相反的区域靠近) |
全局Moran’s I 指数的缺陷
全局莫兰指数可以判断某一属性值在整个研究区域内是否存在自相关性(即属性值在空间上的分布呈离散、集聚或随机),但无法判断是高值集聚还是低值集聚
在 ArcMap 中全局 Moran’s I 分析
在 ArcMap 工具箱中导航:
ArcToolbox > Spatial Statistics Tools > Analyzing Patterns > Moran’s I (Spatial Autocorrelation)
工具参数设置根据需求而定

中间黄色部分为随机分布,右侧为集聚分布,左侧为离散分布
标准化指数(Z 分数)
Z 分数越大:说明观测值离平均值越远,并且偏向于较高的区域。
Z 分数越小:说明观测值离平均值越近,或者偏向较低的区域。
Z 分数为负:说明观测值低于均值
标准化指数(Z-score),表示一个数据点与平均值之间的差距,用标准差来衡量(将不同量纲的数据转化为无量纲数据,便于比较)
在空间分析中,Z 值通常是通过标准化 Moran’s I 来得到的。
通过计算 Z 值,我们可以判断 Moran’s I 是否显著地偏离了零
如果 Z 值 > 1.96 或 Z 值 < -1.96(通常使用 95% 的置信区间),那么 Moran’s I 的结果被认为是显著的,意味着空间数据中存在真实的空间自相关关系。
如果 Z 值接近 0,则说明 Moran’s I 的值可能只是偶然的,不能得出空间自相关的结论
全局空间自相关可以告诉我们某一属性在整体上是聚集、离散还是随机,但是无法告诉我们这些现象发生在哪些具体区域
局部空间自相关
局部空间自相关的分析是对全局空间自相关分析的重要补充,主要用于探究空间数据中具体区域的属性分布情况,定位哪些区域存在显著的聚集、离散或随机现象。这种分析有助于揭示空间数据中局部模式,例如高值集聚、低值集聚或异常值
局部 Moran’s I
通过衡量每个空间单元与其邻近区域之间的相似性来判断局部空间自相关

-
i>0:表示区域 i 与其邻接区域有正向空间自相关,可能是高值聚集或低值聚集。
-
i<0:表示区域 i 与其邻接区域有负向空间自相关,形成高-低反转或低-高反转模式。
-
i=0:表示区域 i 的属性值与邻接区域没有显著的自相关关系,可能是随机分布
如果局部 Moran’s I 为正且显著,ArcMap 会根据每个区域的属性值及其邻接区域的属性值,决定是 高值聚集(High-High) 还是 低值聚集(Low-Low)
在 ArcMap 中局部 Moran’s I 分析
Spatial Statistics Tools > Mapping Clusters > Generate Spatial Weights Matrix-
Z 值:标准化后的 Z 分数,用于评估局部 Moran’s I 是否显著。
-
p 值:用于测试 Moran’s I 的显著性
冷热点分析
Spatial Statistics Tools > Mapping Clusters > Hot Spot Analysis (Getis-Ord Gi*)
冷热点分析(Hot Spot Analysis)主要用于确定区域内的“热点”区域(Hot Spots)和“冷点”区域(Cold Spots),即属性值较高或较低的区域



