基于WOA鲸鱼优化的NARMAX模型参数辨识算法MATLAB仿真,对比PSO优化算法
目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
4.1 NARMAX模型定义
4.2 鲸鱼优化算法WOA原理
4.3 粒子群优化算法PSO原理
5.完整程序
1.程序功能描述
基于WOA鲸鱼优化的NARMAX模型参数辨识算法MATLAB仿真,对比PSO优化算法。分别通过WOA和PSO两种优化算法,对NARMAX模型进行参数辨识,对比优化收敛性能和参数辨识误差。
2.测试软件版本以及运行结果展示
MATLAB2022A/MATLAB2024B版本运行

3.核心程序
.............................................................for j=1:Dif rand_flag<0.5 if abs(K1)>=1RLidx = floor(Num*rand()+1);X_rand = xwoa(RLidx, :);D_X_rand = abs(K2*X_rand(j)-xwoa(i,j)); xwoa(i,j)= X_rand(j)-K1*D_X_rand; elseD_Leader = abs(K2*woa_idx(j)-xwoa(i,j)); xwoa(i,j)= woa_idx(j)-K1*D_Leader; endelsedistLeader = abs(woa_idx(j)-xwoa(i,j));xwoa(i,j) = distLeader*exp(6*l).*cos(l.*6*pi)+woa_idx(j);end%目标函数更新if xwoa(i,j)>=tmps(j,2) xwoa(i,j)=tmps(j,2);endif xwoa(i,j)<=tmps(j,1) xwoa(i,j)=tmps(j,1);endendend% 记录当前迭代的种群最佳适应度值Ysave(t) =1/(1+woa_get);% 记录当前迭代的种群最佳位置Xsave(:,t)=woa_idx; % 绘制种群最佳适应度值随迭代次数的变化曲线
figure
plot(1:Iters,Ysave,'LineWidth',2);
% 绘制种群最佳位置各分量随迭代次数的变化曲线
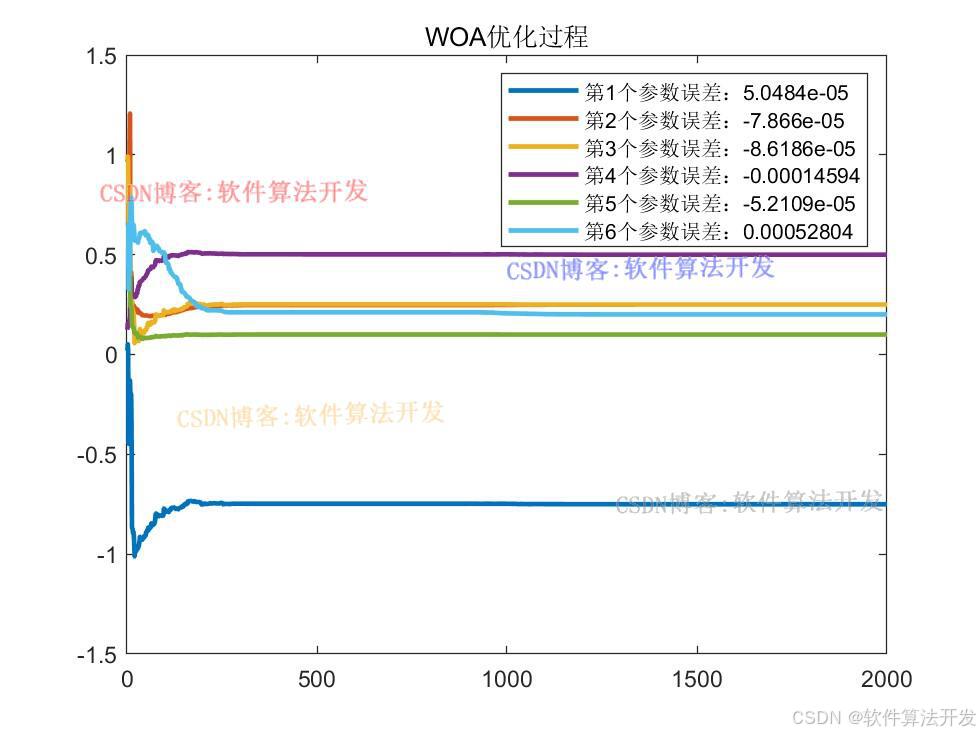
title('WOA优化过程');
err=Xsave(:,end)-theta0';figure
plot(1:Iters,Xsave,'LineWidth',2);
legend(['第1个参数误差:',num2str(err(1))],['第2个参数误差:',num2str(err(2))],['第3个参数误差:',num2str(err(3))],['第4个参数误差:',num2str(err(4))],['第5个参数误差:',num2str(err(5))],['第6个参数误差:',num2str(err(6))]);
title('WOA优化过程'); save R2.mat Iters Ysave Xsave err
1014.本算法原理
非线性自回归滑动平均外生输入(NARMAX)模型是一种广泛应用于非线性系统建模的工具,能够描述系统的动态特性。然而,NARMAX 模型的参数辨识是一个复杂的非线性优化问题。鲸鱼优化算法(WOA)和粒子群优化算法(PSO)都是常用的智能优化算法,可用于解决这类参数辨识问题。
4.1 NARMAX模型定义
NARMAX模型可以表示为:
y(k)=F[y(k−1),⋯,y(k−ny),u(k−1),⋯,u(k−nu),e(k−1),⋯,e(k−ne)]+e(k)
其中,y(k) 是系统在时刻 k 的输出,u(k) 是系统在时刻 k 的输入,e(k) 是系统在时刻 k 的噪声,ny、nu 和 ne 分别是输出、输入和噪声的阶数,F 是一个非线性函数。
在本文中,我们考虑一个简化的6参数NARMAX模型,假设其形式为:
y(k)=θ1y(k−1)+θ2y(k−2)+θ3u(k−1)+θ4u(k−2)+θ5y(k−1)u(k−1)+θ6+e(k)
其中,θ=[θ1,θ2,θ3,θ4,θ5,θ6]T 是待辨识的参数向量。
4.2 鲸鱼优化算法WOA原理
鲸鱼优化算法是一种受座头鲸觅食行为启发的元启发式优化算法。座头鲸主要通过气泡网捕食策略来寻找猎物,WOA模拟了这一行为,包括包围猎物、螺旋更新位置和随机搜索等过程。
算法步骤
初始化:随机初始化鲸鱼种群的位置X(0),设置最大迭代次数T、种群数量 Nwhales 等参数。
计算适应度:计算每个鲸鱼的适应度值,即目标函数J(θ)的值。
找到最优解:找到当前种群中适应度值最小的鲸鱼,将其位置作为当前最优解X∗(t)。
更新系数向量:更新 a、A和C。
更新位置:根据∣A∣的值,选择包围猎物、螺旋更新位置或随机搜索方式更新鲸鱼的位置。
判断终止条件:如果达到最大迭代次数T,则停止迭代,输出最优解;否则,返回步骤2。
4.3 粒子群优化算法PSO原理
粒子群优化算法是一种基于群体智能的优化算法,通过模拟鸟群或鱼群的群体行为来寻找最优解。每个粒子代表一个潜在的解,在搜索空间中飞行,根据自身的历史最优位置和群体的历史最优位置来更新自己的位置。
算法步骤
初始化:随机初始化粒子的位置X(0) 和速度V(0),设置最大迭代次数T、种群数量Nparticles、惯性权重w、学习因子c1和c2等参数。
计算适应度:计算每个粒子的适应度值,即目标函数J(θ)的值。
更新个体最优和全局最优:更新每个粒子的历史最优位置Pi 和群体的历史最优位置Pg。
更新速度和位置:根据速度和位置更新公式更新粒子的速度和位置。
判断终止条件:如果达到最大迭代次数T,则停止迭代,输出最优解;否则,返回步骤2。
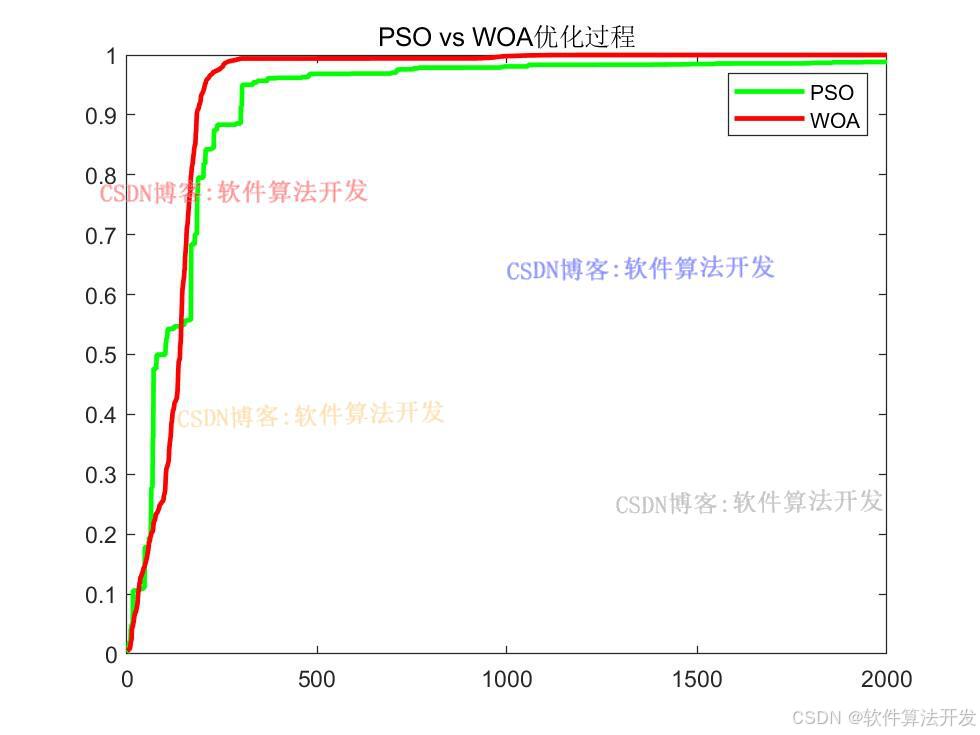
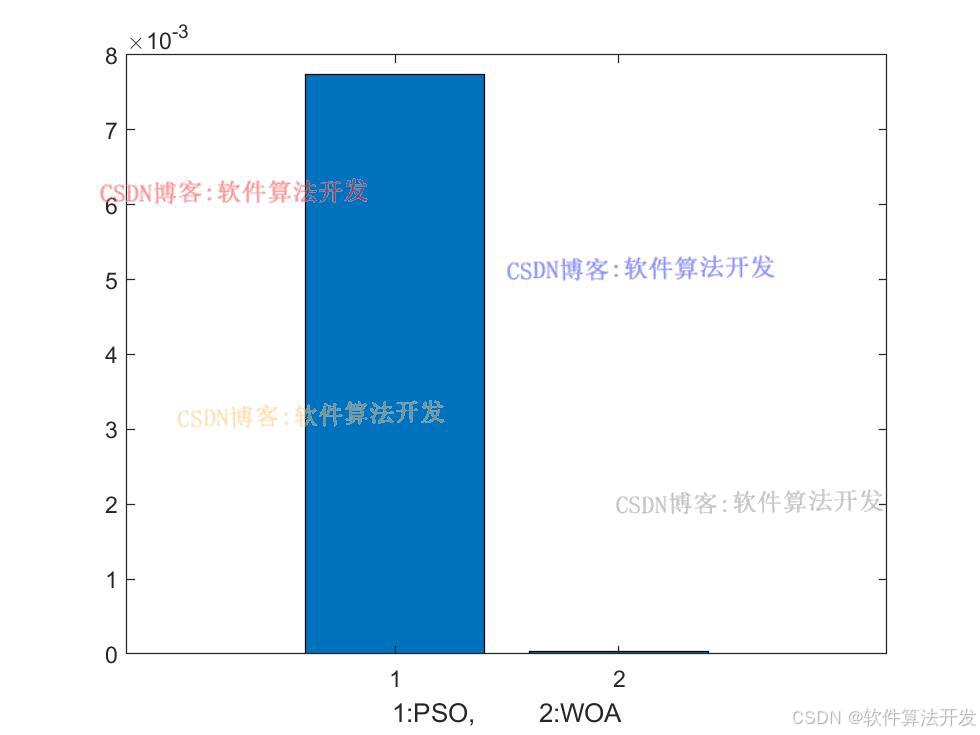
基于WOA鲸鱼优化的NARMAX模型参数辨识算法和基于PSO的参数辨识算法都可以用于解决NARMAX模型的参数辨识问题。WOA具有较强的全局搜索能力和较好的鲁棒性,能够在复杂的非线性优化问题中找到更优的解。
5.完整程序
VVV
