【漫话机器学习系列】211.驻点(Stationary Points)
驻点(Stationary Points):理解函数导数为零的关键位置
在数学分析、机器学习优化、物理建模等领域中,驻点(Stationary Points)是一个非常重要的概念。它们是函数图像中“停下来的点”,即导数为零的点,往往也是我们寻找极值(最大值、最小值)或判断函数走向变化的关键。
本文将借助图示,深入解析驻点的定义、几种类型、判断方法及其在优化中的实际应用。
什么是驻点?
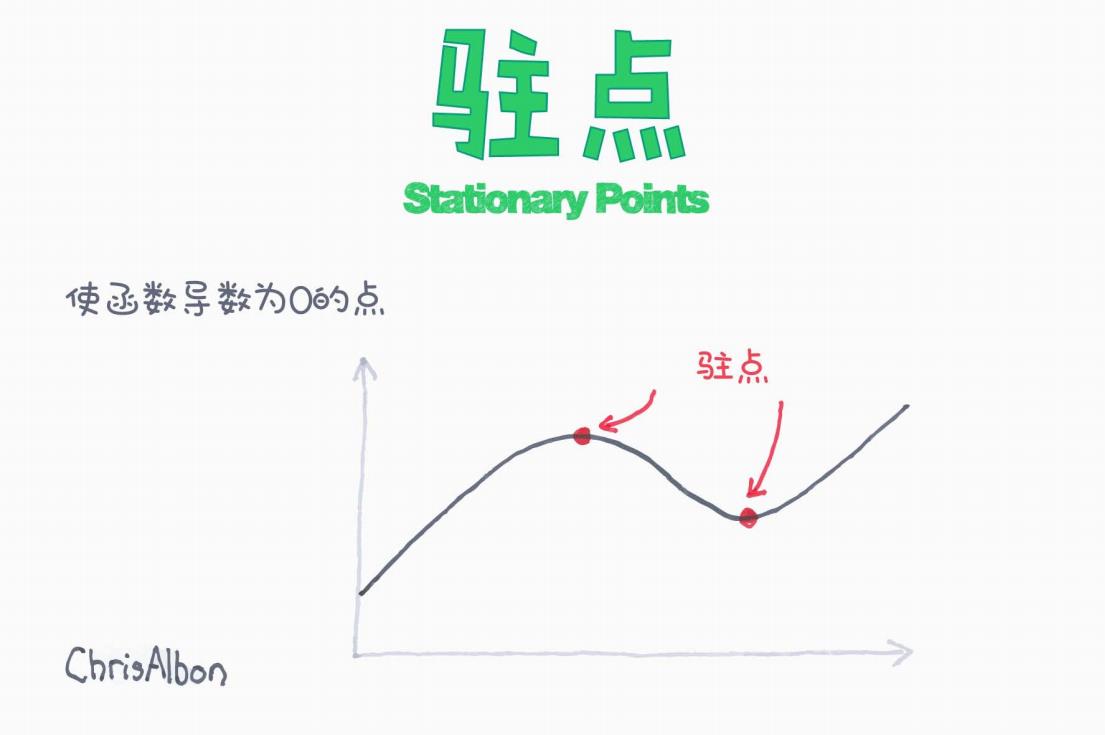
如上图所示,驻点是函数导数为零的点,也就是说,在这些点上,函数的切线斜率为零,图像“平坦”下来。
数学上,如果函数 f(x) 可导,则当:
时,点 就是函数的一个驻点。
图中红色标注的两个点,就是典型的驻点,一个对应“局部极大值”,一个对应“局部极小值”。
为什么驻点重要?
驻点常常是我们寻找函数最值的起点。在优化问题中,例如我们希望最小化某个损失函数,首先就需要找到所有导数为 0 的点(即驻点),然后进一步判断这些点中哪些是真正的最小值。
此外,驻点在以下几个方面扮演重要角色:
-
数学分析:寻找极值、拐点、函数走向
-
机器学习:损失函数的最优解
-
物理建模:平衡点、临界状态
-
图形绘制:绘制函数图像的高光点
驻点 ≠ 极值点!
需要注意的是:并不是所有驻点都是极值点。
驻点分为三类:
-
极大值点:例如图中左侧的红点,函数先增后减,此处为局部最高点;
-
极小值点:例如图中右侧的红点,函数先减后增,为局部最低点;
-
拐点或鞍点:函数在此“短暂停留”但并没有达到极值,例如
在 x = 0 处就是一个鞍点。
因此,要判断一个驻点的性质,必须结合二阶导数或其他方法进一步分析。
如何判断驻点的类型?
方法一:使用二阶导数判别法:
设 ,且 f 可导两次。
-
如果
,则
为局部极小值;
-
如果
,则
为局部极大值;
-
如果
,需要更高阶导数或其他方法判断(如变号法)。
方法二:使用变号法:
观察导数 f'(x) 在驻点左右的符号:
-
从正变负:极大值;
-
从负变正:极小值;
-
不变号或变号多次:鞍点或其他非极值驻点。
驻点在机器学习中的应用
驻点在机器学习优化中是核心概念之一,尤其是在使用梯度下降(Gradient Descent)等算法时:
-
每一步更新模型参数,就是沿着梯度方向“逼近”导数为零的驻点;
-
驻点可能是目标函数的局部最小值,也可能是全局最小值或鞍点;
-
深度学习中的“鞍点困境”即大量驻点并不是极小值,使训练陷入停滞。
图示讲解
图中简洁地展示了一个典型函数曲线,两个红点即为导数为零的驻点:
-
左侧红点:局部极大值(导数从正变负)
-
右侧红点:局部极小值(导数从负变正)
总结
| 项目 | 内容 |
|---|---|
| 定义 | 函数导数为零的点 f'(x) = 0 |
| 判断方法 | 二阶导数法、变号法 |
| 类型 | 极大值、极小值、鞍点 |
| 应用 | 函数极值、机器学习优化、物理建模等 |
小结一句话
驻点,是函数“暂时停止变化”的位置,是通向极值与最优解的必经之地。
