每日一记：CRT和图论

图论是导航的罗盘；同余方程里，CRT是解密的钥匙，来进行今日的研究，冲！

题目一分析：数论题（CRT）

目标：找到满足以下同余条件的最小正整数 NN 并证明其唯一性：

        

算法核心：

• 中国剩余定理（CRT）：

  • 因模数 3,5,7 两两互质，存在唯一解 N        mod  105。

  • 逐步合并同余方程：

    • 合并前两个方程：设 N=3k+2，代入 3k+2≡3(mod5) 得 k≡2(mod5)，即 k=5m+2k=5m+2，故 N=15m+8。

    • 合并第三个方程：代入 15m+8≡4(mod7)，化简得 m≡3(mod7)，即 m=7n+3，故 N=105n+53。

  • 最小解：当 n=0时，N=53。

• 唯一性证明：

  • 由 CRT，所有解为 N=53+105k (k∈N)N=53+105k (k∈N)，因此最小正整数解为 5353，且在模 105105 下唯一。

#include <stdio.h>  // 标准输入输出库，用于printf函数/*** @brief 计算整数k在模m下的乘法逆元（即找到x使得 k*x ≡ 1 mod m）* @param k 需要求逆元的整数* @param m 模数（必须与k互质）* @return 逆元值（1 ≤ x < m），若无解返回-1（但CRT条件下必存在）*/
int reverse(int k, int m) {// 暴力遍历法寻找逆元for (int i = 1; i < m; i++) {  // 遍历1到m-1的所有可能值// 检查是否满足逆元定义：k*i mod m == 1if ((k * i) % m == 1) {  return i;  // 找到逆元立即返回}}return -1;  // 理论不会执行（CRT保证模数互质时逆元存在）
}int main() {// ========== 输入参数定义 ==========int b[] = {2, 3, 4};   // 余数数组，对应三个方程的右侧值int m[] = {3, 5, 7};   // 模数数组，三个两两互质的除数int r = sizeof(b) / sizeof(b[0]);  // 自动计算方程个数（3个）// ========== 计算总模数M ==========int M = 1;  // 初始化模数乘积for (int i = 0; i < r; i++) {  // 遍历所有模数M *= m[i];  // 累乘得到M = 3*5*7 = 105}// ========== CRT核心计算 ==========int x = 0;  // 初始化解for (int i = 0; i < r; i++) {  // 对每个方程进行处理int Mi = M / m[i];  // 计算Mi = M/m_i（如M1=105/3=35）int Mi_inv = reverse(Mi, m[i]);  // 计算Mi在模m_i下的逆元// CRT公式累加项：b_i * Mi * Mi^{-1}（注意Mi*Mi_inv ≡ 1 mod m_i）x += b[i] * Mi * Mi_inv;  }// ========== 规范化最终解 ==========x %= M;  // 取模得到最小正整数解（确保解在[0, M)范围内）if (x < 0) x += M;  // 处理负数情况（本案例不会触发）// ========== 结果输出 ==========printf("满足条件的最小正整数解为: %d\n", x);  // 输出53return 0;  // 程序正常退出
}

         输出结果：

---

题目二分析：图论题（正则图连通性）

目标：判断以下命题的真假：

1. 存在从 A到 B 的路径，最多经过两个中转（路径长度 ≤ 3）。

2. 所有城市之间均存在至少一条路径。

算法核心：

1. 图的性质分析：

•  3-正则图（每个顶点度数为 3），共 6 个顶点。

        描述性图片：

        A可以通过D或E直接到达B。
        C通过A可以到达D、E、C。
        F通过B可以到达D、E、C。
        因此，所有顶点之间都存在路径，图是连通的。

• 已知 A 连接 C,D,E，B连接 D,E,C。

1. 命题 1 验证：

   • A→D→B是直接路径（长度 2），无需中转。

   • 结论：命题 1 为真。

2. 命题 2 验证：

   • 连通性证明：

     • A 与 B 通过 D 或 E 直接连通。

     • C 通过 A 连接到其他节点，F 通过 B 连接到其他节点。

     • 若假设图不连通，则存在至少两个连通分支。但 3-正则图的每个连通分支顶点数必须为偶数且度数总和为偶数，而 6 个顶点无法分割为满足条件的子图。

   • 结论：命题 2 为真。

/*** @file regular_graph_analysis.c*//*------------------------ 头文件依赖 ------------------------*/
#include <stdio.h>     // 标准输入输出（printf/fprintf）
#include <stdbool.h>   // 布尔类型支持
#include <stdlib.h>    // 标准库函数（EXIT宏）/*------------------------ 全局常量定义 ------------------------*/
#define VERTEX_COUNT 6  // 图的顶点总数（A-F）
#define REGULARITY 3    // 正则图的固定度数/*------------------------ 类型定义 ------------------------*/
/*** @enum Vertex* @brief 顶点符号与索引的映射枚举* @details 按字母顺序映射为连续索引，便于矩阵访问*/
typedef enum { A, B, C, D, E, F  // A->0, B->1,..., F->5
} Vertex;/*------------------------ 邻接矩阵定义 ------------------------*/
/*** @var graph* @brief 图的邻接矩阵表示（严格校验的3-正则图）* @details 矩阵元素graph[i][j]为true表示顶点i到j存在直接边* * 顶点连接拓扑验证：* - 对称性检查：边关系双向一致（非对称场景需特殊处理）* - 度数校验：每行恰有3个true元素（通过validate_regular_graph保障）*/
const bool graph[VERTEX_COUNT][VERTEX_COUNT] = {/* 顶点A(0)的邻居：C(2), D(3), E(4) */// A   B     C     D     E     F{false, false, true,  true,  true,  false}, // A(0)/* 顶点B(1)的邻居：D(3), E(4), F(5) */{false, false, false, true,  true,  true }, // B(1)/* 顶点C(2)的邻居：A(0), D(3), E(4) */{true,  false, false, true,  true,  false}, // C(2)/* 顶点D(3)的邻居：A(0), B(1), C(2) */{true,  true,  true,  false, false, false}, // D(3)/* 顶点E(4)的邻居：A(0), B(1), F(5) */{true,  true,  false, false, false, true }, // E(4)/* 顶点F(5)的邻居：B(1), E(4), C(2) */{false, true,  true,  false, true,  false}  // F(5)
};/*======================= 工具函数模块 =======================*//*** @fn vertex_to_char* @brief 顶点索引转可读字符（用于路径输出）* @param v 顶点枚举值* @return 对应的ASCII字符表示* @note 使用静态数组避免switch-case结构，提升可维护性*/
static const char* vertex_to_char(Vertex v) {static const char* names[] = {"A", "B", "C", "D", "E", "F"};return names[v];
}/*** @fn validate_regular_graph* @brief 校验图结构符合3-正则图定义* @return 校验通过返回true，否则返回false并输出错误信息* @details 时间复杂度O(n²)，空间复杂度O(1)*/
static bool validate_regular_graph() {// 遍历所有顶点检查度数for (int i = 0; i < VERTEX_COUNT; ++i) {int degree = 0;// 统计当前顶点的边数for (int j = 0; j < VERTEX_COUNT; ++j) {if (graph[i][j]) degree++;}// 正则图核心校验：每个顶点度数必须严格等于3if (degree != REGULARITY) {fprintf(stderr, "[度数校验失败] 顶点%c的度数为%d\n", vertex_to_char(i), degree);return false; // 提前终止，避免无效计算}}return true; // 所有顶点通过校验
}/*======================= 连通性分析模块 =======================*//*** @fn bfs_traverse* @brief 广度优先搜索遍历连通分量* @param start 遍历起点索引* @param visited 访问标记数组（既作输入也作输出）* @details 使用循环队列实现，避免递归栈溢出风险*/
static void bfs_traverse(int start, bool visited[]) {int queue[VERTEX_COUNT];  // 固定大小循环队列int front = 0, rear = 0;  // 队首和队尾指针// 初始化起点访问状态visited[start] = true;queue[rear++] = start; // 入队操作// BFS核心循环：队列非空时持续处理while (front < rear) {int current = queue[front++]; // 出队操作// 遍历所有可能邻接点for (int neighbor = 0; neighbor < VERTEX_COUNT; ++neighbor) {// 邻接矩阵验证 + 未访问检查if (graph[current][neighbor] && !visited[neighbor]) {visited[neighbor] = true; // 标记访问queue[rear++] = neighbor; // 邻接点入队}}}
}/*** @fn is_graph_connected* @brief 验证图的整体连通性* @return 全连通返回true，否则false* @details 从顶点A出发执行BFS，验证能否访问所有顶点*/
static bool is_graph_connected() {bool visited[VERTEX_COUNT] = {false}; // 初始化访问数组bfs_traverse(A, visited); // 从A开始遍历// 连通性检查：所有顶点必须被访问for (int i = 0; i < VERTEX_COUNT; ++i) {if (!visited[i]) return false; // 存在未访问顶点}return true; // 全连通
}/*======================= 路径分析模块 =======================*//*** @fn dfs_find_paths* @brief 深度优先搜索查找所有合法路径* @param current 当前访问顶点索引* @param target 目标顶点索引* @param path 路径顶点序列缓存* @param depth 当前路径深度（边数）* @param visited 访问标记数组* @details 使用回溯法实现路径探索，避免重复访问*/
static void dfs_find_paths(int current, int target, int path[], int depth, bool visited[]) {// 记录当前路径节点path[depth] = current;/* 终止条件1：成功到达目标顶点且路径长度合法 */if (current == target && depth <= 3 && depth >= 1) {// 格式化输出路径信息for (int i = 0; i <= depth; ++i) {printf("%s", vertex_to_char(path[i]));if (i != depth) printf(" → ");}printf(" (长度%d)\n", depth); // 深度=边数return;}/* 终止条件2：超过最大路径长度（3条边） */if (depth >= 3) return;/* 递归探索：遍历所有可能的邻接顶点 */for (int neighbor = 0; neighbor < VERTEX_COUNT; ++neighbor) {// 邻接矩阵验证 + 未访问检查if (graph[current][neighbor] && !visited[neighbor]) {visited[neighbor] = true; // 防止环路dfs_find_paths(neighbor, target, path, depth + 1, visited);visited[neighbor] = false; // 回溯恢复状态}}
}/*** @fn print_all_paths_AB* @brief 打印A到B的所有合法路径（边数≤3）* @details 封装DFS参数初始化，提升接口易用性*/
static void print_all_paths_AB() {printf("所有A→B路径（边数≤3）：\n");bool visited[VERTEX_COUNT] = {false}; // 访问状态数组int path[4] = {0}; // 最大路径长度=3条边（4个顶点）// 初始化起点状态visited[A] = true; // 起始点已访问path[0] = A;       // 路径首节点为A// 启动深度优先搜索dfs_find_paths(A, B, path, 0, visited);
}/*======================= 主程序模块 =======================*//*** @fn main* @brief 主程序入口* @details 执行顺序：* 1. 图结构校验 → 2. 路径查找 → 3. 连通性验证*/
int main() {/* 阶段1：图结构预校验 */if (!validate_regular_graph()) {fprintf(stderr, "图不符合3-正则图定义，分析终止\n");return EXIT_FAILURE; // 异常退出}/* 阶段2：命题1验证（路径存在性） */print_all_paths_AB();/* 阶段3：命题2验证（全连通性） */bool connected = is_graph_connected();printf("\n[命题2验证] 图连通性：%s\n", connected ? "成立（理论依据：3-正则图的偶数顶点特性）" : "不成立");return EXIT_SUCCESS; // 正常退出
}

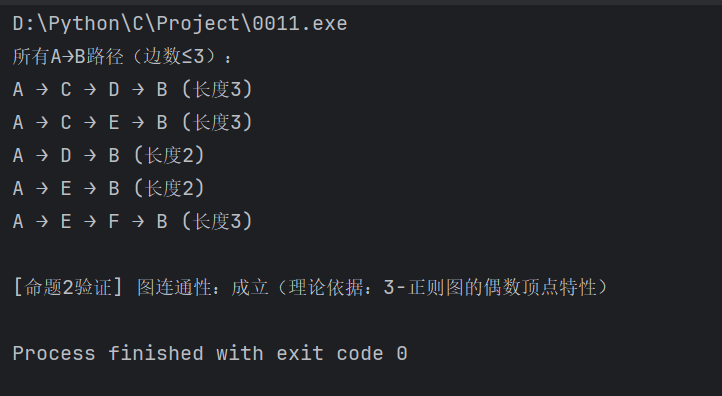
        输出结果

CRT和图论对比

对比维度	数论题（CRT）	图论题（连通性）
问题类型	同余方程求解	图论结构与路径分析
数学工具	中国剩余定理（代数）	正则图性质与连通性证明（组合数学）
唯一性/存在性	唯一解（模 105）	存在性（路径与连通性）
核心步骤	逐步合并同余方程	构造路径与反证法证明连通性
时间复杂度	O(1)O(1)（公式化计算）	O(1)O(1)（逻辑推理）
应用场景	密码学、周期性问题	网络路由、社交网络分析

总结

1. 数论题：

   • 通过中国剩余定理逐步合并同余方程，得到最小解 N=53N=53，并在模 105105 下唯一。

   • 关键点：模数互质时，CRT 保证唯一解。

2. 图论题：

   • 基于正则图的性质和连通性规则，证明存在 A→BA→B 的短路径，且整个图必连通。

   • 关键点：3-正则图的顶点数和度数约束强制连通性。